Consider two identical rings of mass M and radius R fixed on a horizontal axis in a gravity - free space. A particle of mass m is held at rest at the centre of 1st ring and projected along the axis towards 2nd ring. The minimum speed of projection so that the particle reaches the centre of 2nd ring is
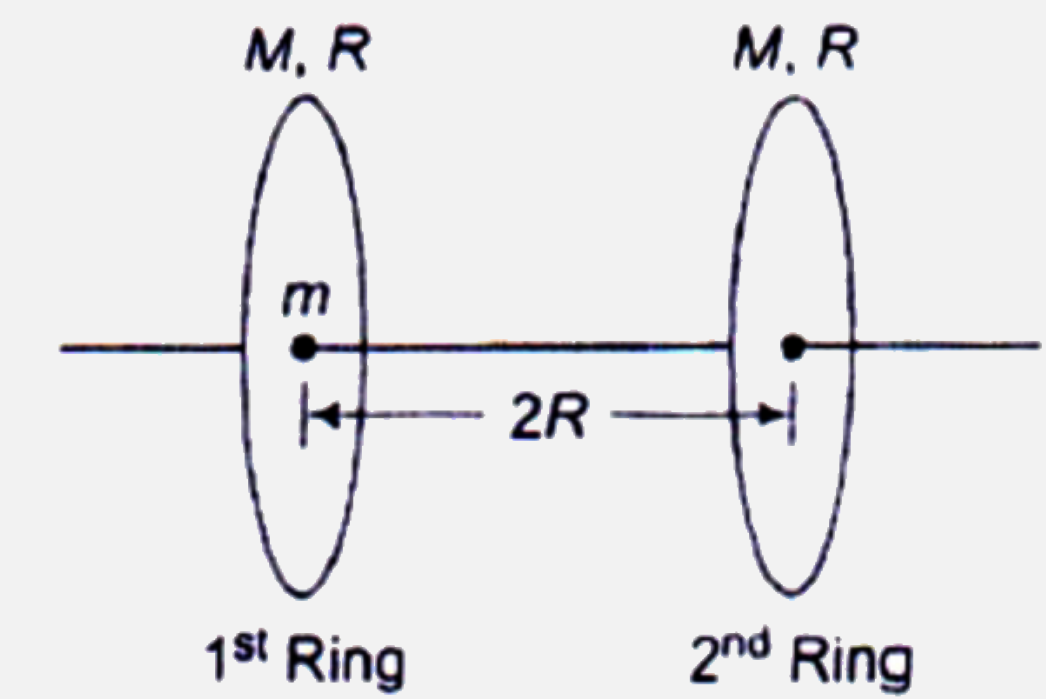
√GMR
√2GMR
⎷2GMR(1+1√5−√2)
⎷GMR(1+√5−1√2)
The correct Answer is:C
Step by step video & image solution for Consider two identical rings of mass M and radius R fixed on a horizontal axis in a gravity - free space. A particle of mass m is held at rest at the centre of 1^("st") ring and projected along the axis towards 2^("nd") ring. The minimum speed of projection so that the particle reaches the centre of 2^("nd") ring is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
A√GMaB√GM2a(mM)C√GM2a(Mm)D√GMa(MM+m)Consider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
AGmr2B2Gm√3r2C2Gm3√3r2DGm2r2
A ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionRing of mass M and radius 1m placed on smooth horizontal surface at rest. A particle of same mass M moving horizontally with speed 6m/s strike the ring and stick to it as shown in figure. Find angular speed of system after collision in rad/sec.

View SolutionA circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
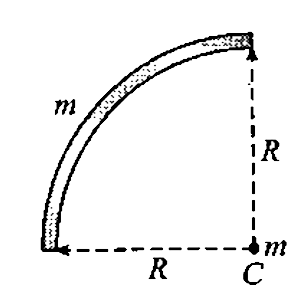
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
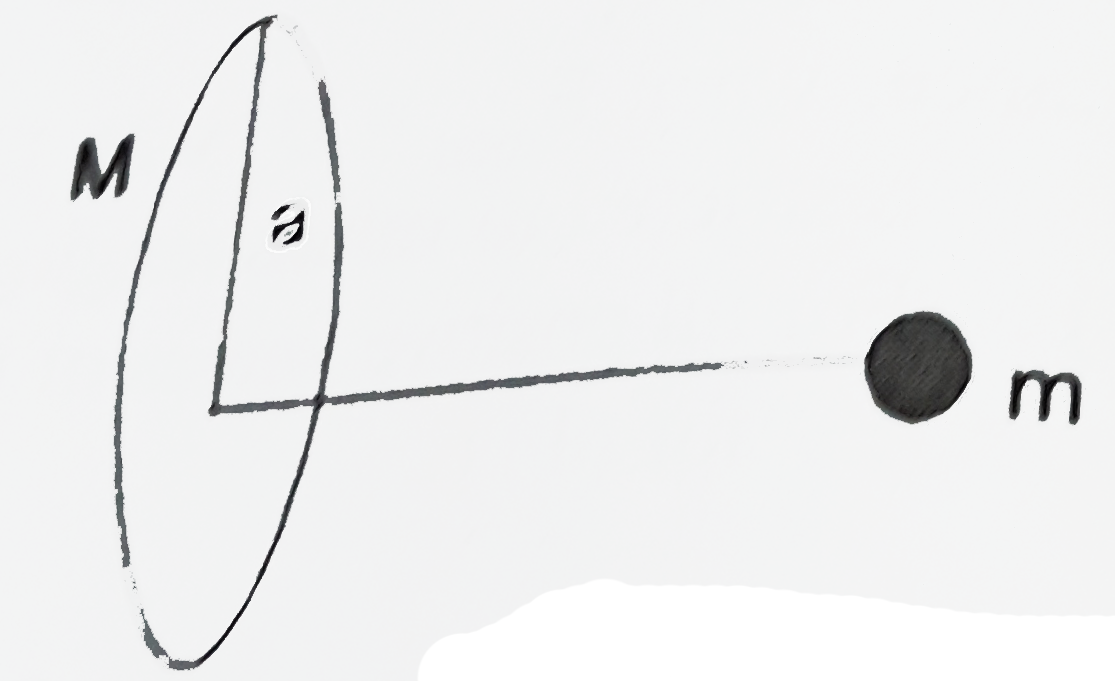
if x<<a, the particle of mass m will:
View Solution


