A circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
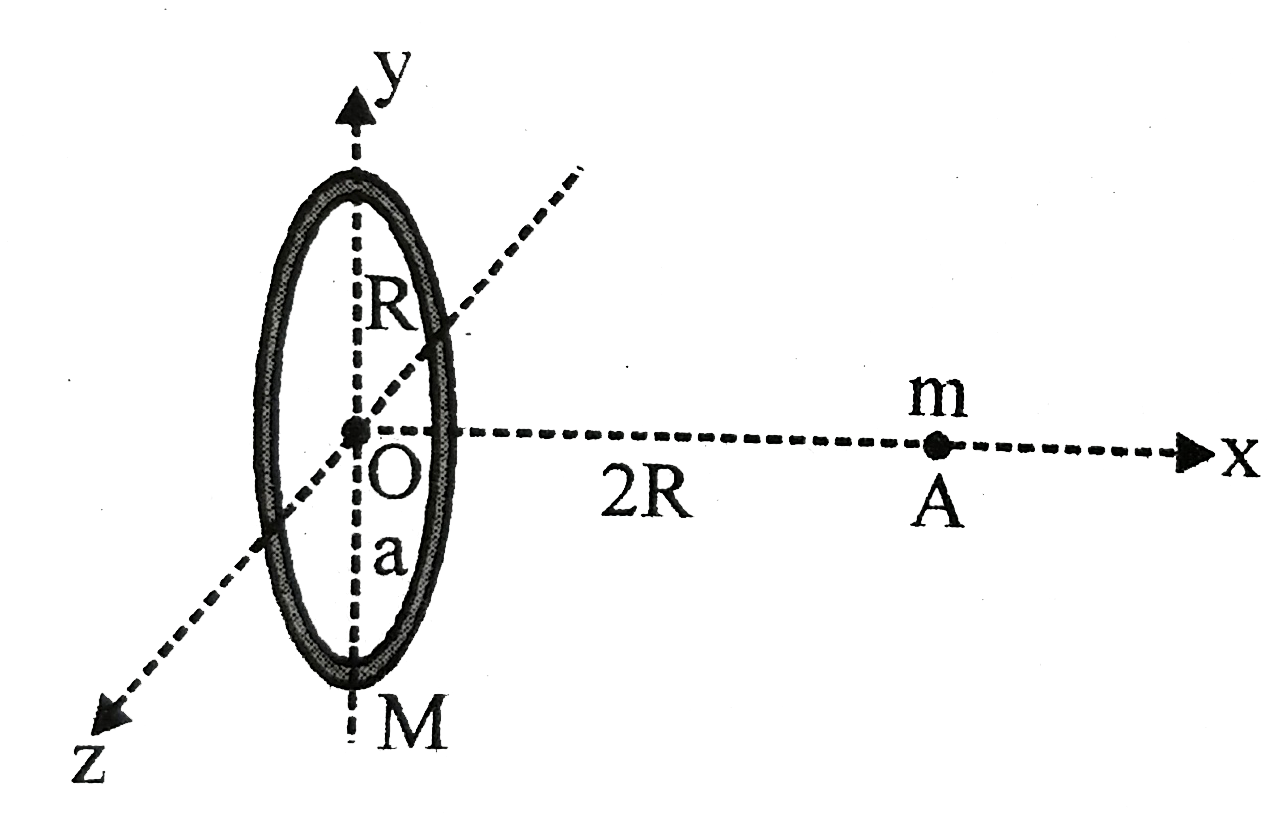
As shown in figure, first we find potential at A due to the ring, it is given as
VA=−GM√R2+(2R)2=−GM√5R
Now potential at origin O due to ring is
V0=−GMR
When m moves from A to O, work done on it due to gravitational force is
W=m(VA−V0)=m(−GM√5R+GMR)
=GMmR(√5−1√5)
This work done gravitational force on m must be equal to the increase in kinetic energy of the mass m, thus we have
12mv2=(√5−1√5)GMmR
or v=⎡⎢
⎢⎣2(√5−1)GM√5R⎤⎥
⎥⎦1/2
This problem can also be solved simply by using energy conservation. Thus initially when m was at rest at point A2 the total energy of system is only gravitational potential energy given as
Ei=m.VA=−GMm√5R
Finally when m pass through O, the total energy of system is
Ef=12mv2+mV0
=12mv2−GMmR
As no external work is done on the system in this case, the total energy of system must be conserved, thus according to energy conservation we have
Ei=Ef
−GMm√5R=12mv2−GMmR
v=⎡⎢
⎢⎣2(√5−1)GM√5R⎤⎥
⎥⎦1/2
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Solved Example8videos
GRAVITATION
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Practice Exercise18videos
GRAVITATION
- BOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)8videos
CENTRE OF MASS & MOMENTUM CONSERVATION
- BOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise89videos
HEAT TRANSFER
Similar Questions
The gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
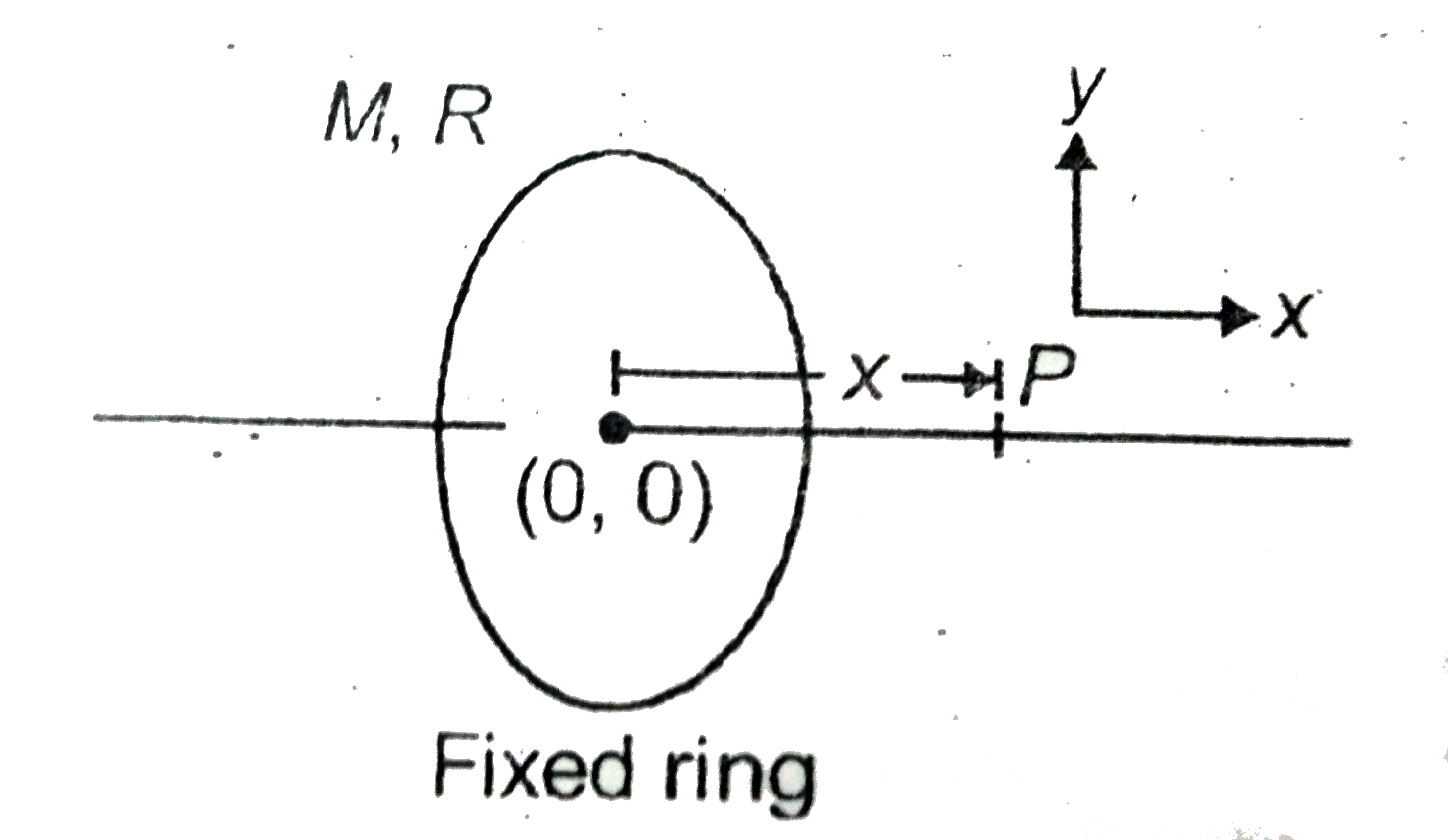
If the particle (mass m) is released from rest from a point distant x=R√3, then it will pass through the centre of ring with speedView SolutionConsider a nebula in the form of a ring of radius R and mass M. A star of mass m(mR from the centre of the ring on its axis, initially at rest.The speed with which it crosses the centre of the ring is y=√(p−√q)GMR . Find (p+q)
View Solution
Knowledge Check
- Question 1 - Select One
A point P(R√3,0,0) lies on the axis of ring of mass M and radius R the ring is located in YZ plane with its centre at origin O A small particle of mass m starts from P and reaches O under gravitatinal attracton only its speed at O will be
A√GMRB√GmRC√Gm2RD√Gm√2R - Question 2 - Select One
A ring with a uniform charge Q and radius R, is placed in the yz plane with its centre at the origin
Athe field at the origin is zeroBThe potential at the origin is kQRCthe potential at the origin is kQx2Dthe filled at the point (x,0,0) is kQR2+x2 - Question 3 - Select One
A point P(R√3,0,0) lies on the axis of a ring of mass M and radius R. The ring is located in yx-plane with its centre at origin O. A small particle of mass m starts from P and reaches O under gravitational attraction only. Its speed at O will be
A√GMRB√GmRC√GM2RD√2m√2R
Consider two identical rings of mass M and radius R fixed on a horizontal axis in a gravity - free space. A particle of mass m is held at rest at the centre of 1st ring and projected along the axis towards 2nd ring. The minimum speed of projection so that the particle reaches the centre of 2nd ring is
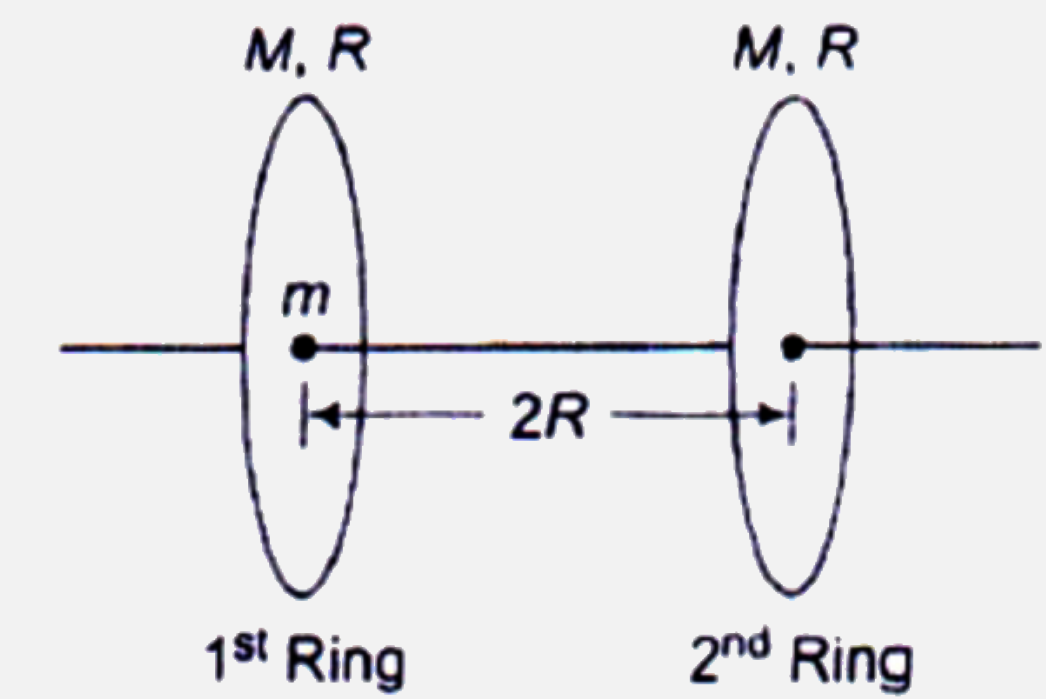 View Solution
View SolutionA point P (R√3m,0,) lies on the axis of a ring of mass M and radius R. The ring is located in y−z plane with its centre at origin. A small particle of mass m start from P and reaches O under gravitational attraction only. Its speed at O will be.
View SolutionA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
View SolutionFor a uniform ring of mass M and radius R at its centre
View Solution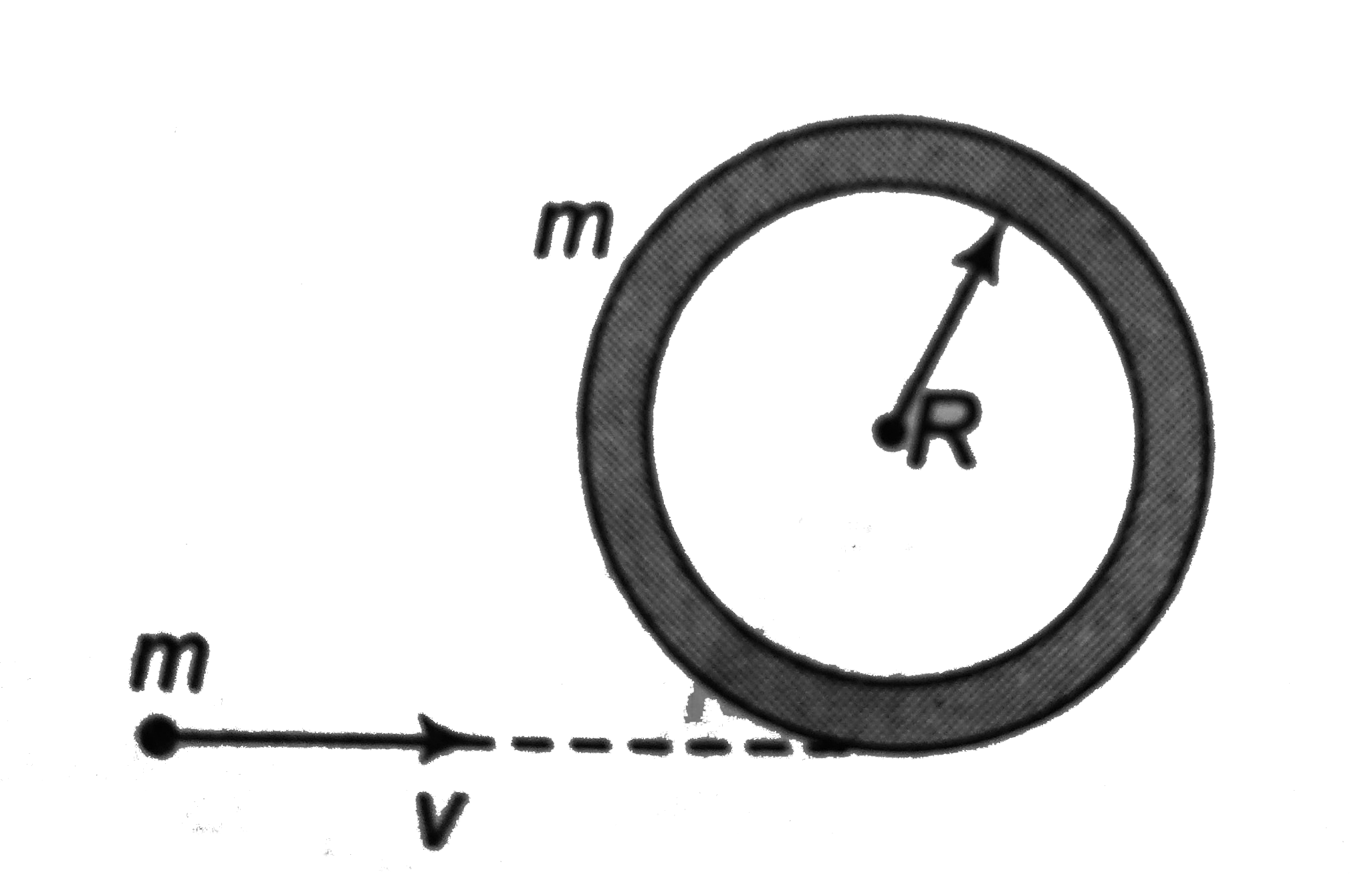
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring isView Solution

