A wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
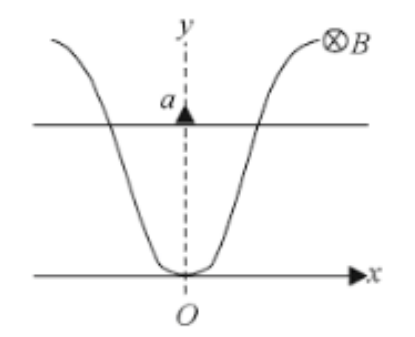
By√(2a)k
By√4ak
By√8ak
By√ak
The correct Answer is:C
Step by step video & image solution for A wire bent as a parabola y=kx^(2) is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A wire bent as a parabola y=ax2 is located in a uniformed magnetic field of induaction B , the vector B being perpendicular to the plane x−y . At moment t=0 a connector starts sliding translationwise from the parabola apex with a constant acceleration ω . Find the emf of electromagnetic induction in the loop thus formed as a function of y

View SolutionA conducting rod is bent as a parabola y=Kx2, where K is a constant and it is placed in a unifrom magnetic field of induction B. At t=0 a conductor of resistance per unit length λ starts sliding up on the parabola with a constant acceleration a and the parabolic frame starts rotating with constant angular frequency ω about the axis of symmetry, as shown in the figure. Find the instantaneous current induced in the rod, when the frame turns through π/4rad.
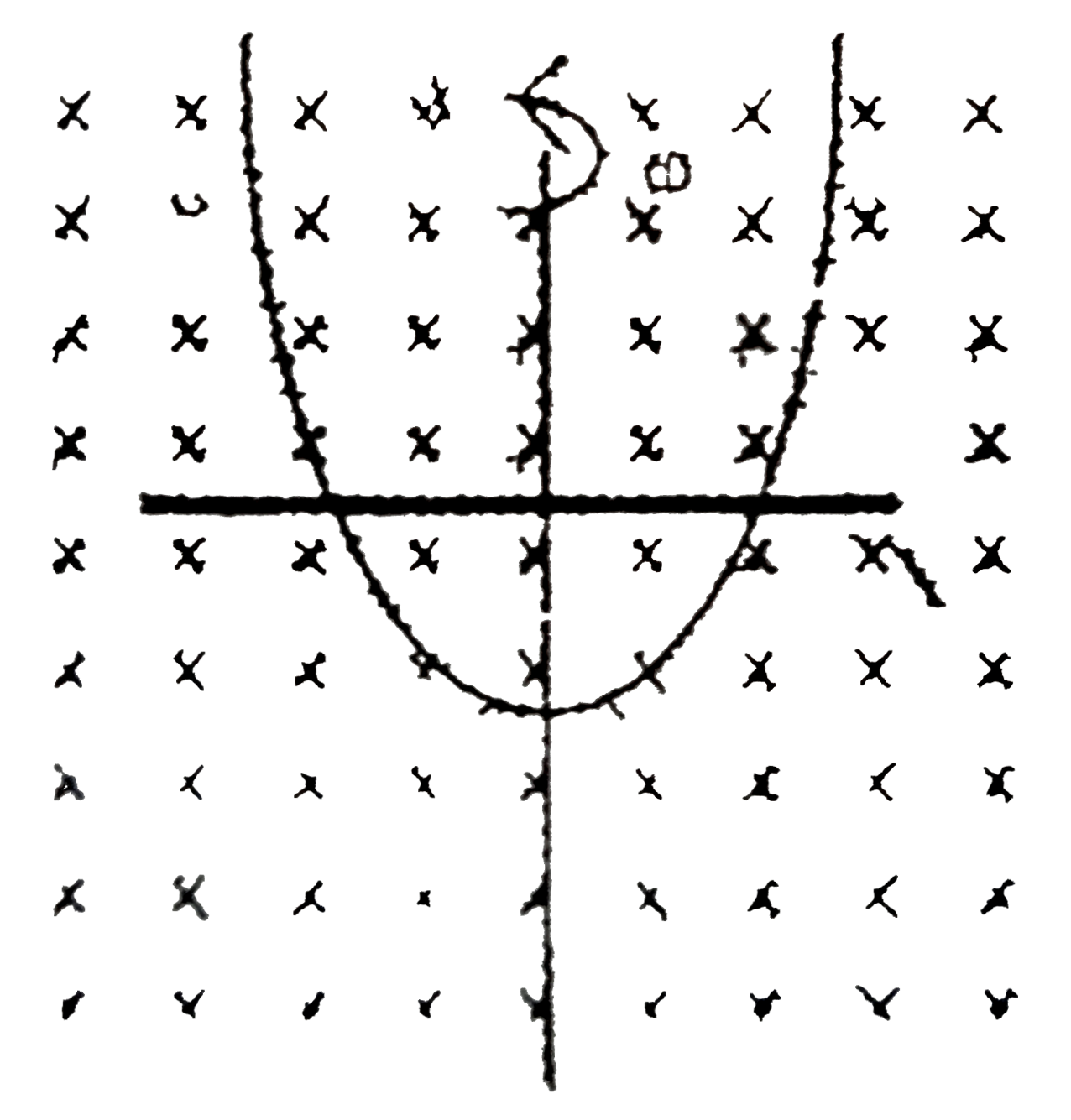
View Solution
Knowledge Check
A wire is bent in the form of a V shape and placed in a horizontal plane. There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
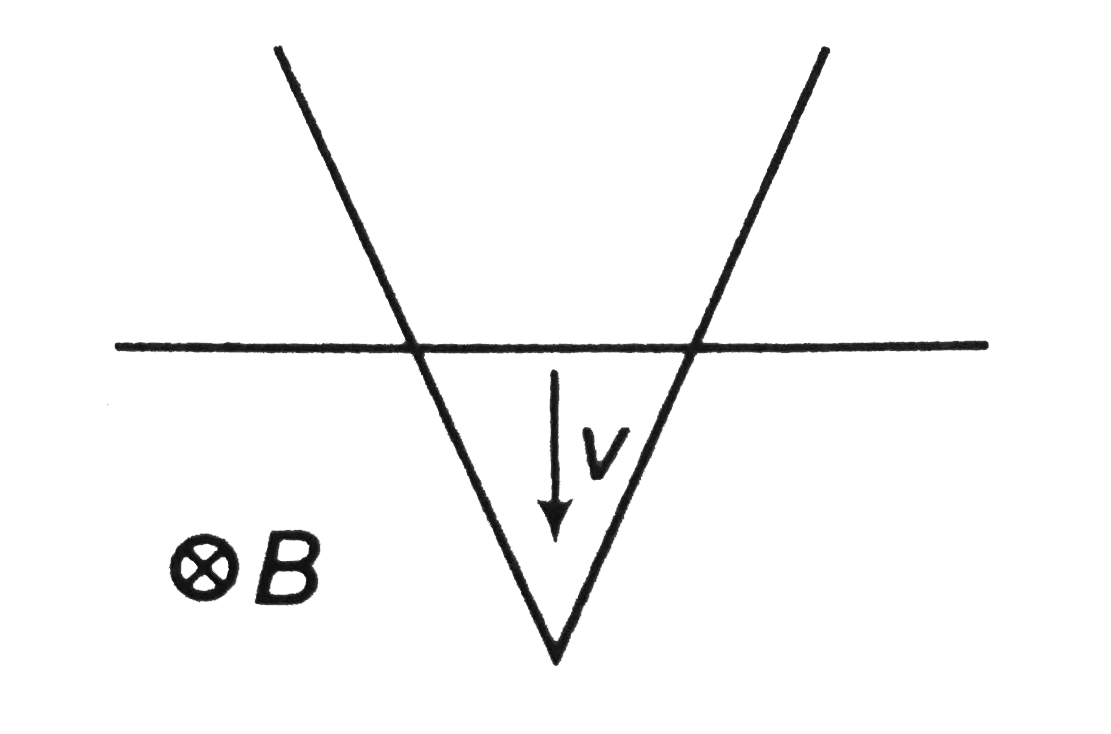 Aincrease with timeBdecrease with timeCremain constantDalways be zero
Aincrease with timeBdecrease with timeCremain constantDalways be zeroThe graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conductig loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude fo the emf induced in the loop, greater first
 Ab>(d=e)<(a=c)Bb>(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)
Ab>(d=e)<(a=c)Bb>(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)The graph gives the magnitude B (t) of a uniform magnetic field that exists throughout a conducting loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first
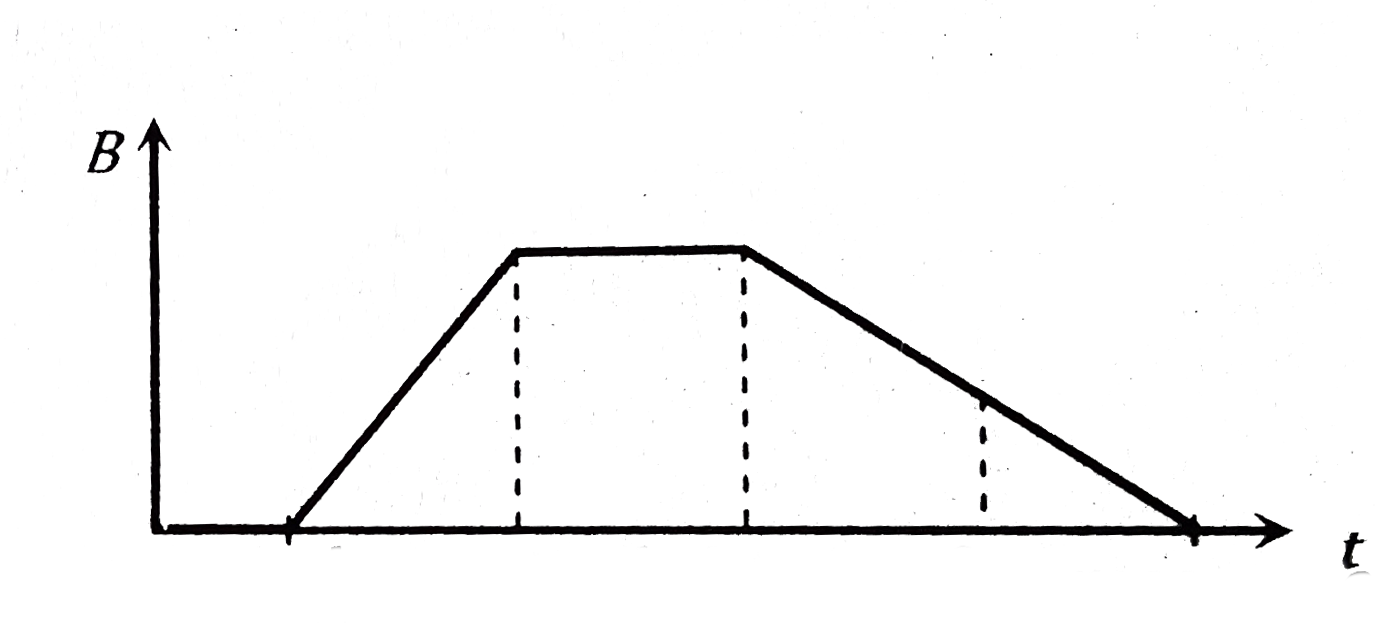 Ab>(d=e)<(a=c)Bb<(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)
Ab>(d=e)<(a=c)Bb<(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)
A wire loop enclosing a semi-circle of radius a=2cm is located on the boundary of a uniform magnetic field of induction B=1T (figure).At the moment t=0 the loop is set into rotation with a constant angular acceleration β=2rad/sec2 about an axis O coinciding with a line of vector B on the boundary.The emf induced in the loop as a function of time t is [x×10−4(−1)n×t]V, where n=1,2,... is the number of the half-revolution taht the loop performs at the given moment t.Find the value of x.(The arrow in the figure shows the emf direction taken to be positive, at t=0 loop was completely outside)

View SolutionA conducing circular loop is placed in a uniform magnetic field of 0.02 T, woth its plane perpendicular to the field. If the redius of the loop starts shrinking at a constant rate of 1.0mm/s, then find the emf induced in the loop, at the instant when radius is 4 cm.
View SolutionA wire loop enclosing as semicircle of radius R is located on the boudary of uniform magnetic field B. At the moment t=0, the loop is set into rotation with a costant angular acceleration α about an axis O coinciding with a line of vector B on the boundary. Find the emf induced in the loop as a function of time. Draw the approximate plot of this function.The arrow in the figure shows the emf direction taken to be positive.
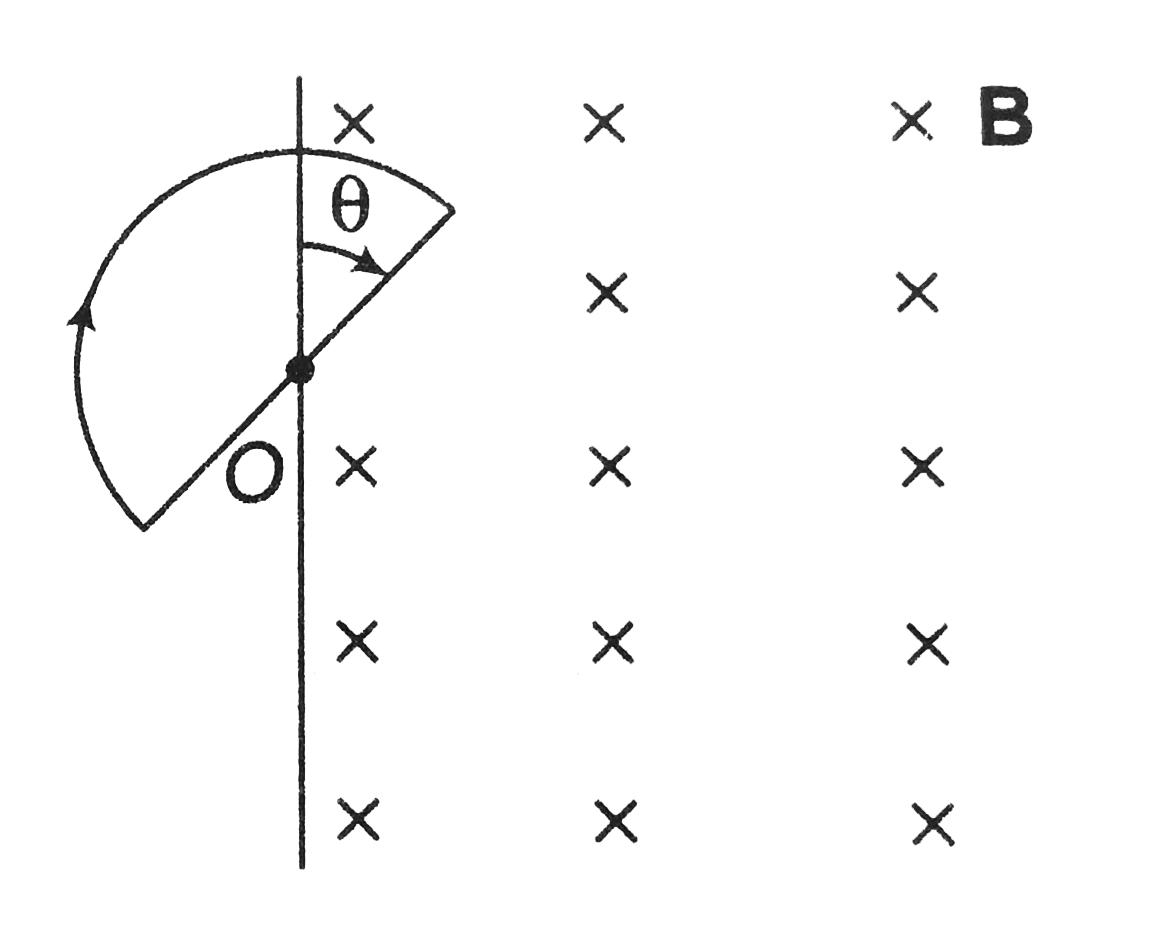
View SolutionThe graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, with the direction of the field perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first.
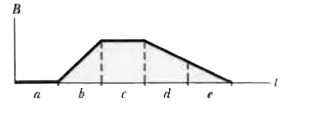
View SolutionA conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0 mm s^(-1). Find the induced emf in the loop at an instant when the radius is 2 cm.
View Solution
