A small particle of mass m and its retaining cord is spinning with angular velocity ω on the horizontal suface of a smooth disc. As force F is slightly relaxed, r increases and ω changes.
Determine the rate of change of ω with respect to r
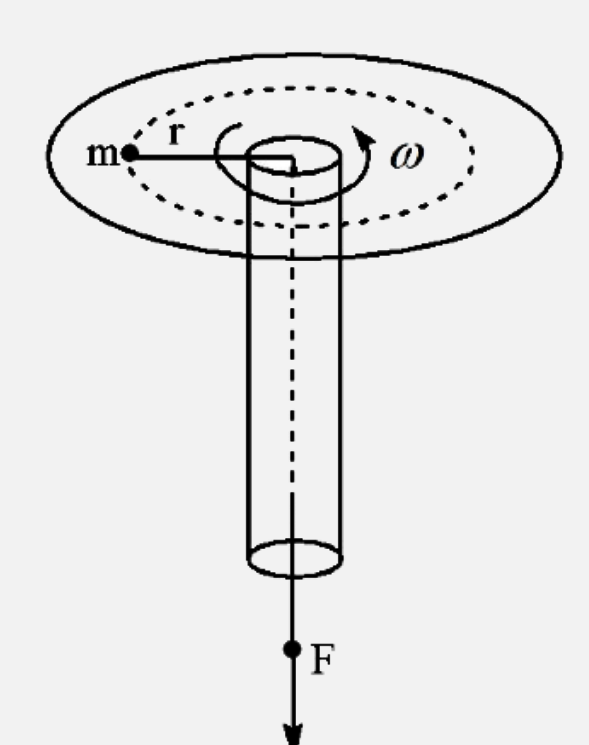
+ωr
−ωr
−2ωr
+2ωr
The correct Answer is:C
Step by step video & image solution for A small particle of mass m and its retaining cord is spinning with angular velocity omega on the horizontal suface of a smooth disc. As force F is slightly relaxed, r increases and omega changes. Determine the rate of change of omega with respect to r by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View Solution
Knowledge Check
If a small babyof mass m is moving with angular velocity ω in a circle of radius r, then its K.E. will be
Amωr2B(mω2r)Cmω2r22Dmωr22As shown in the figure, a disc of mass m is rolling without slipping with angular velocity ω. When it crosses point B disc will be in
 Atranslational motion onlyBpure rolling motionCrotational motion onlyDnone of these
Atranslational motion onlyBpure rolling motionCrotational motion onlyDnone of theseA particle moving along a circule path of radius 'r' with uniform angular velocity ω. Its angular acceleration is
Arω2Br/ωCzeroDω/r
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then :
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is

View SolutionThe rate change of angular velocity w.r to t in uniform circular motion is a
View Solution
