A horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -
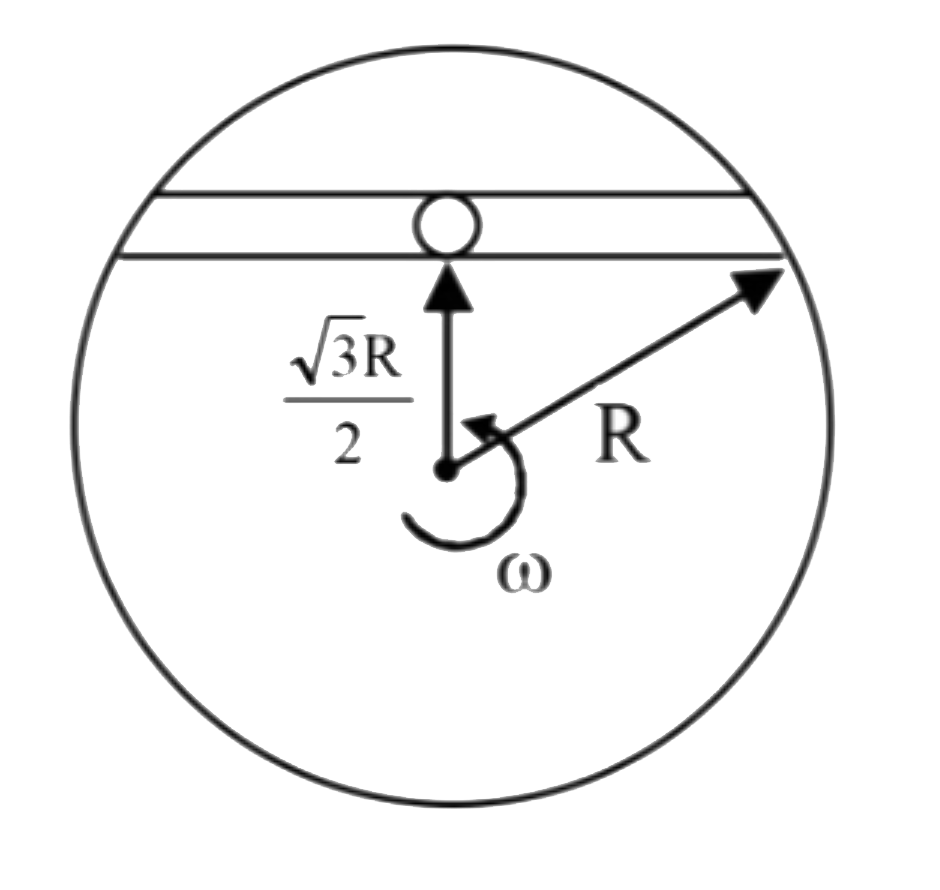
√32ωR
ωR2
ωR
ωR√2
The correct Answer is:A
Step by step video & image solution for A horizontal disk is rotating with angular velocity omega about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View Solution
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
Ano friction exists between te disc and the ringBthe angular momentum of the system is conservedCthe final common angular velocity is 12ωDall of the aboveA disc of mass m and radius r is rotating with angular velocity, on a frictionless horizontal plane about a vertical axis passing through its centre. A ring of same mass and radius is gently placed on it in such a way that centres of both coincide. After some time it is found that both attain a common angular velocity
AIf we consider disc and ring in a single system then its angular momentum is conserved.Bω=ω03CLoss in K.E. is double to that of final K.E. of the systemDLoss in K.E. is 2/3 of initial K.E. of the system.
A particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
View SolutionA charge q is unifromly distributed over the volume of a unifrom ball of mass m and radius R which rotates with an angular velocity ω about the axis passing through its centre. Find the respective magnetic moment and its ratio to the mechanical moment.
View SolutionA copper ball of mass m=1kg with a radius of r=10cm rotates with angular velocity ω=2rad/s about an axis passing through its centre. The work should be performed to increase the angular velocity of rotation of the ball two fold is.
View SolutionAn ice block is in a trough which is rotating about vertical axis passing through its centre. When ice melts completely, the angular velocity of the system
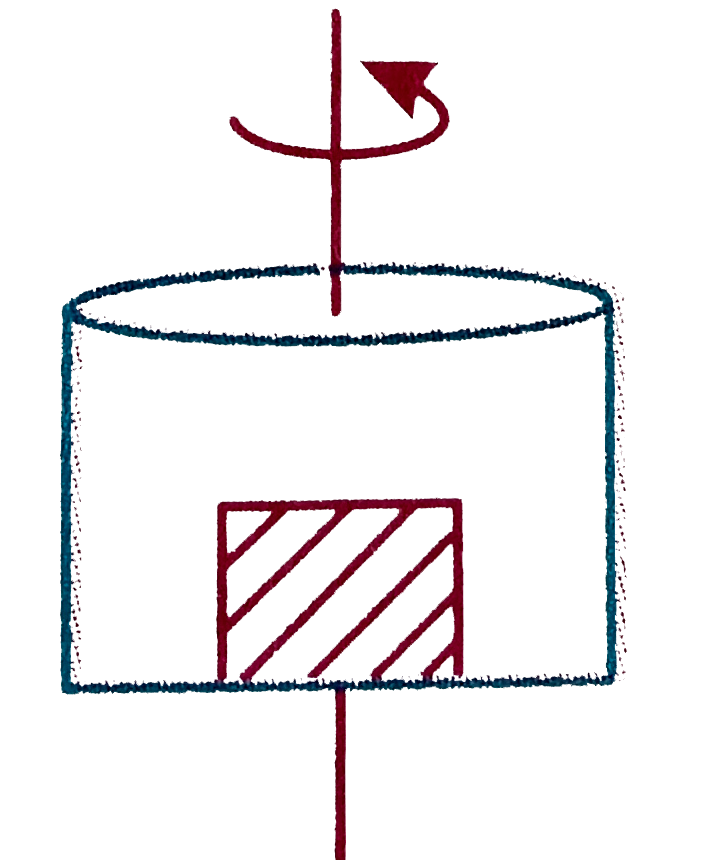
View SolutionA horizontal platform is rotating with uniform angular velcity around the vertical axis passing through its centre. At some instant of time a viscous fluid of mass m is dropped at the centre and is allowed to spread out and finally fall. The angular velocity during this period :
View Solution
