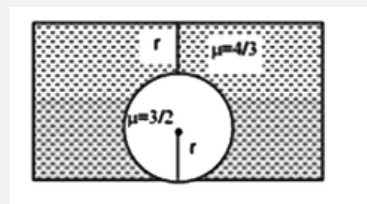
A glass sphere having refractive index (3/2) is having a small irregularity at its centre. It is placed in a liquid of refractive index 43 such that the surface of the liquid is at a distance r above the sphere, where r = 20 cm is radius of the sphere, where r = 20 cm is radius of the sphere. If the irregularity is viewed from above then what is it's distance (in cm) from the centre where eye will observed the irregularity?
The correct Answer is:13
Step by step video & image solution for A glass sphere having refractive index (3/2) is having a small irregularity at its centre. It is placed in a liquid of refractive index (4)/(3) such that the surface of the liquid is at a distance r above the sphere, where r = 20 cm is radius of the sphere, where r = 20 cm is radius of the sphere. If the irregularity is viewed from above then what is it's distance (in cm) from the centre where eye will observed the irregularity? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
ArB0.5 rC√0.6rD√0.4rA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10V. The potential at the distance 3cm from the centre of the sphere is:
AzeroB10VCsame as at point 5 cm away from the surfaceDsame as at a point 25cm away from the surfaceThere is a small air bubble at the centre of a solid glass sphere of radius 'r' and refractive index μ. What wil be the apparent distance of the bubble from the centre of the sphere, when viewed from outside?
ArBrμCr(1−1μ)DZero
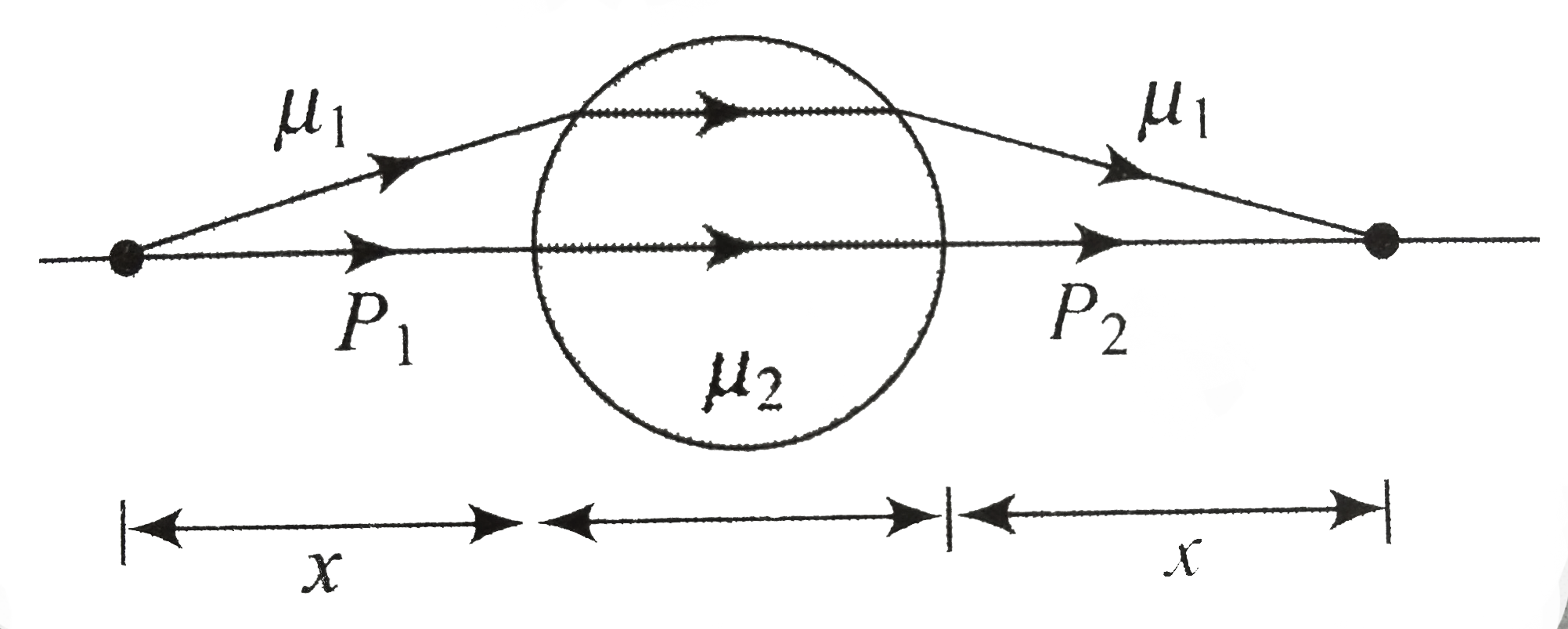
A sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionThe potential at a distance R/2 from the centre of a conducting sphere of radius R will be
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionA hollow metal sphere of radius 5cm is charged such that the potential on its surface is 10V. The potential at a distance of 2cm from the centre of the sphere
View Solution
