If a stone s thrown at a point which is at a distance d away and at a height h above the point from where the stone starts, then what is the value of initial speed u if the stone is lauched at angle θ?
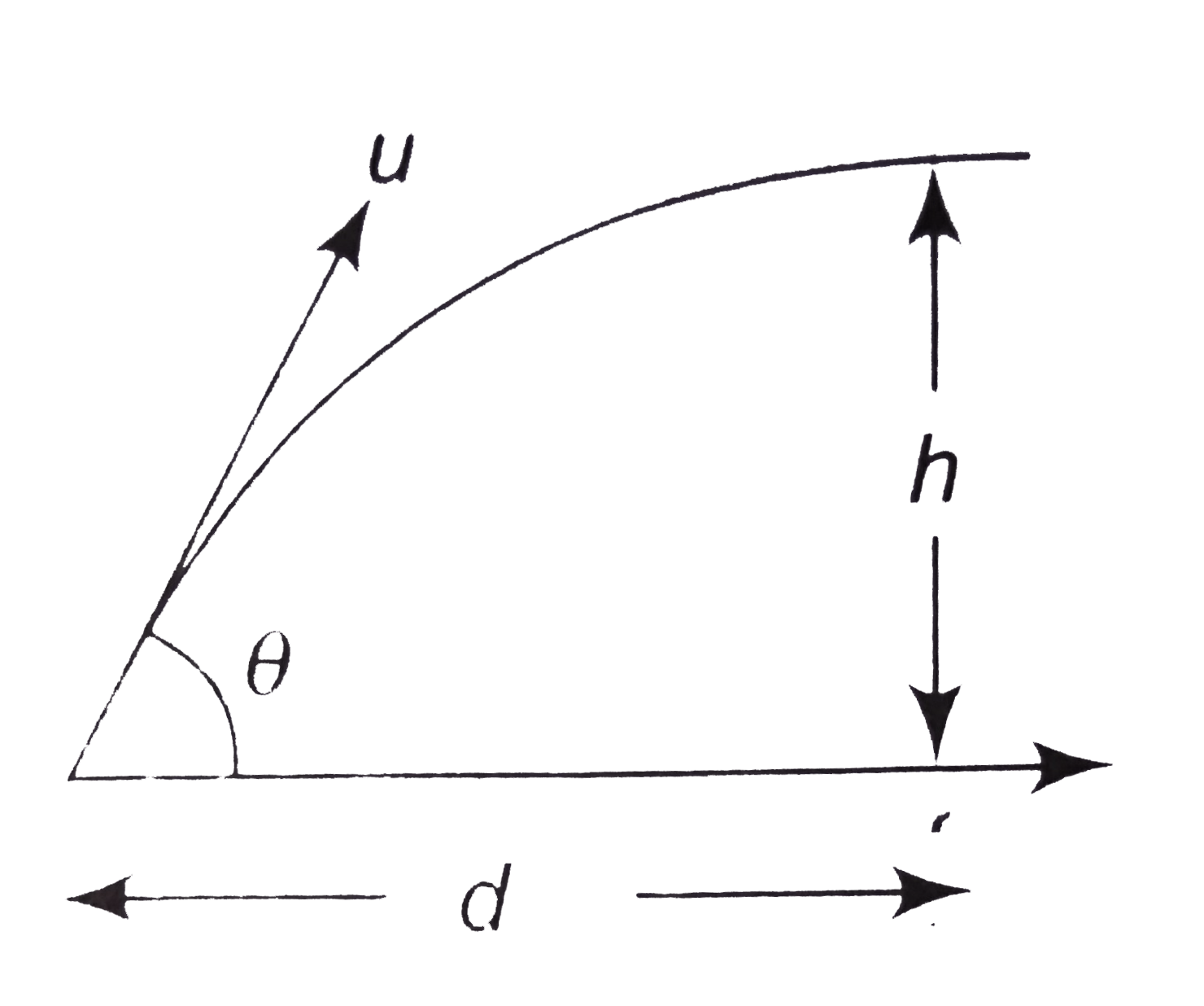
gcostheat√d2(dtanθ−h)
dcosθ√g2(dtanθ−h)
√gd2hcos2θ
√gd2(d−h)
The correct Answer is:B
Step by step video & image solution for If a stone s thrown at a point which is at a distance d away and at a height h above the point from where the stone starts, then what is the value of initial speed u if the stone is lauched at angle theta? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
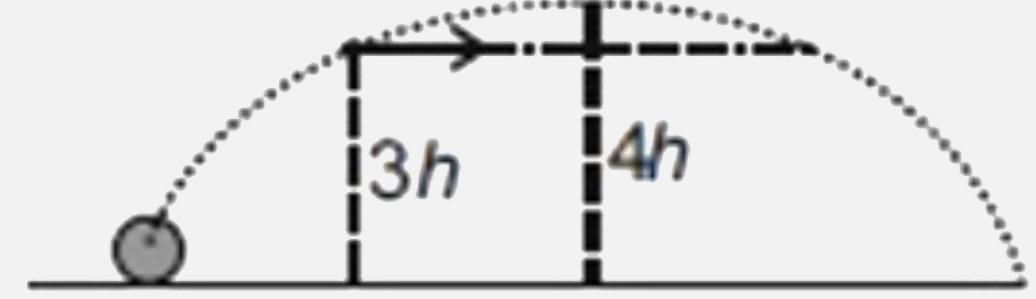
A stone is projected from a point on the ground in such a way so as to hit a bird at height 3h and could attain a maximum height 4h above the ground. If at the instant of projection, the bird flies away horizontally with speed 10ms−1 and the stone still hits the bird while descending, then the horizontal velocity of stone is
View SolutionIf a stone is to hit at a point which is at a horizontal distance 100 m away and at a hight 50 m above the point from where the stone starts, then what is the value of initial speed u if the stone is launched at an angle 45∘?
View Solution
Knowledge Check
If a ston s to at a point which is at a distance d away and at a height h avove the point from where the stone starts, then what is the value of initial speed u if the stone is lauched at angle θ?
 Agcosθ√d2(dtanθ−h)Bdcosθ√d2(dtanθ−h)C√gd2(hcos2θ)D√gd2(d−h)
Agcosθ√d2(dtanθ−h)Bdcosθ√d2(dtanθ−h)C√gd2(hcos2θ)D√gd2(d−h)If a stone is to hit at a point which is at a distance d away and at a height h (see fig) above the point from where the stone starts,then what is the value of initial speed u if the stone is launched at an angle θ?
 Adsinθ√g2(dtanθ−h)Bdcosθ√g2(dtanθ−h)C√gdhcos2θD√gd(d−h)
Adsinθ√g2(dtanθ−h)Bdcosθ√g2(dtanθ−h)C√gdhcos2θD√gd(d−h)If a stone is to hit at a point which is at a distance d away and at a height h (Fig. 5.200) above the point from where the stone starts, then what is the value of initial speed u if the stone is launched at an angle θ ?
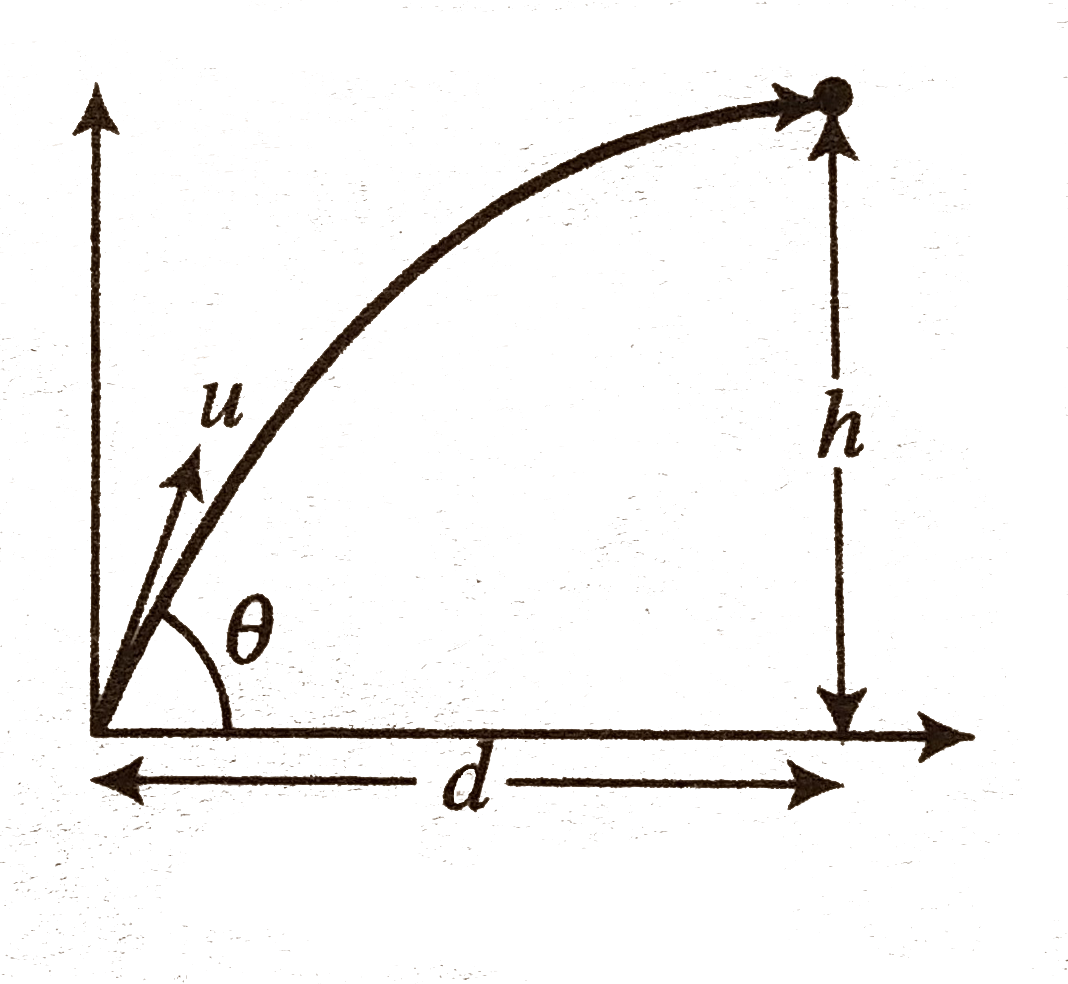 .Agcosθ√d2(dtanθ−h)Bdcosθ√g2(dtanθ−h)C√gd2hcos2θD√gd2d−h
.Agcosθ√d2(dtanθ−h)Bdcosθ√g2(dtanθ−h)C√gd2hcos2θD√gd2d−h
A stone thrown at an angle θ to the horizontal reaches a maximum height h. The time of flight of the stone is :-
View SolutionA person can throw a stone to a maximum distance of h meter. The greatest height to which he can throw the stone is:
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA stone is thrown with a velocity v at an angle θ with the horizontal.Its speed when it makes an angle β with the horizontal is
View SolutionA stone is thrown at an angle θ to the horizontal reaches a maximum height H. Then the time of flight of stone will be:
View Solution
