Two uniformly long charged wires with linear densities and are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine
The correct Answer is:C
To solve the problem, we need to find the slope of the electric field at any point on the line y=√3x due to two charged wires. One wire is placed along the x-axis with linear charge density λ, and the other wire is along the y-axis with linear charge density 3λ.
1. Identify the Electric Field due to Each Wire:
- For an infinite line of charge, the electric field E at a perpendicular distance d from the wire with linear charge density λ is given by:
E=2kλd
where k is Coulomb's constant.
2. Electric Field from the Wire along the X-axis:
- The wire along the x-axis has a linear charge density λ.
- At any point P on the line y=√3x, the perpendicular distance from the x-axis (y = 0) to point P is y=√3x.
- Therefore, the electric field Ex due to this wire at point P is directed upwards (positive y-direction):
Ex=2kλ√3x
3. Electric Field from the Wire along the Y-axis:
- The wire along the y-axis has a linear charge density 3λ.
- The perpendicular distance from the y-axis (x = 0) to point P is x.
- Therefore, the electric field Ey due to this wire at point P is directed away from the wire (positive x-direction):
Ey=2k(3λ)x=6kλx
4. Components of the Electric Field:
- The electric field components at point P are:
- Ex in the y-direction: 2kλ√3x
- Ey in the x-direction: 6kλx
5. Finding the Slope of the Electric Field:
- The slope m of the electric field vector →E at point P can be found using the ratio of the y-component to the x-component:
m=ExEy=2kλ√3x6kλx
- Simplifying this expression:
m=2kλ√3x⋅x6kλ=26√3=13√3
Final Answer:
The slope of the electric field at any point on the line y=√3x is:
13√3
- For an infinite line of charge, the electric field E at a perpendicular distance d from the wire with linear charge density λ is given by:
E=2kλd
where k is Coulomb's constant.
- The wire along the x-axis has a linear charge density λ.
- At any point P on the line y=√3x, the perpendicular distance from the x-axis (y = 0) to point P is y=√3x.
- Therefore, the electric field Ex due to this wire at point P is directed upwards (positive y-direction):
Ex=2kλ√3x
- The wire along the y-axis has a linear charge density 3λ.
- The perpendicular distance from the y-axis (x = 0) to point P is x.
- Therefore, the electric field Ey due to this wire at point P is directed away from the wire (positive x-direction):
Ey=2k(3λ)x=6kλx
- The electric field components at point P are:
- Ex in the y-direction: 2kλ√3x
- Ey in the x-direction: 6kλx
- The slope m of the electric field vector →E at point P can be found using the ratio of the y-component to the x-component:
m=ExEy=2kλ√3x6kλx
- Simplifying this expression:
m=2kλ√3x⋅x6kλ=26√3=13√3
The slope of the electric field at any point on the line y=√3x is:
13√3
Topper's Solved these Questions
Similar Questions
Between two infinitely long wires having linear charge densities λ and −λ there are two points A and B shown in the figure. The amount of work done by the electric field moving a point charge q0 from A to B is equal to
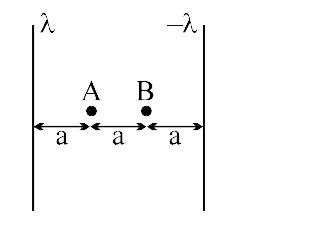
View SolutionIn the figure, OA and OB are two uniformly charged wires, placed along x and y axis respectively. Find the unit vector in the direction of field at point (0,0,√3L).

View Solution
Knowledge Check
Two infinitely long thin styraight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
A2λπε0Bλπε0rCλ2πε0rD3λ2πε0rBetween two infinitely long wires having linear charge densities λ and −λ , there are two points A and B as shown in the figure. The amount of work done by the electric field in moving a point charge q0 from A to B is equal to :
 Aλq02πε0 In 2B−2λq0πesπ0In2C2λq0πε0 IN 2Dλq0πε0 In 2
Aλq02πε0 In 2B−2λq0πesπ0In2C2λq0πε0 IN 2Dλq0πε0 In 2An infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
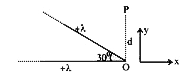 Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
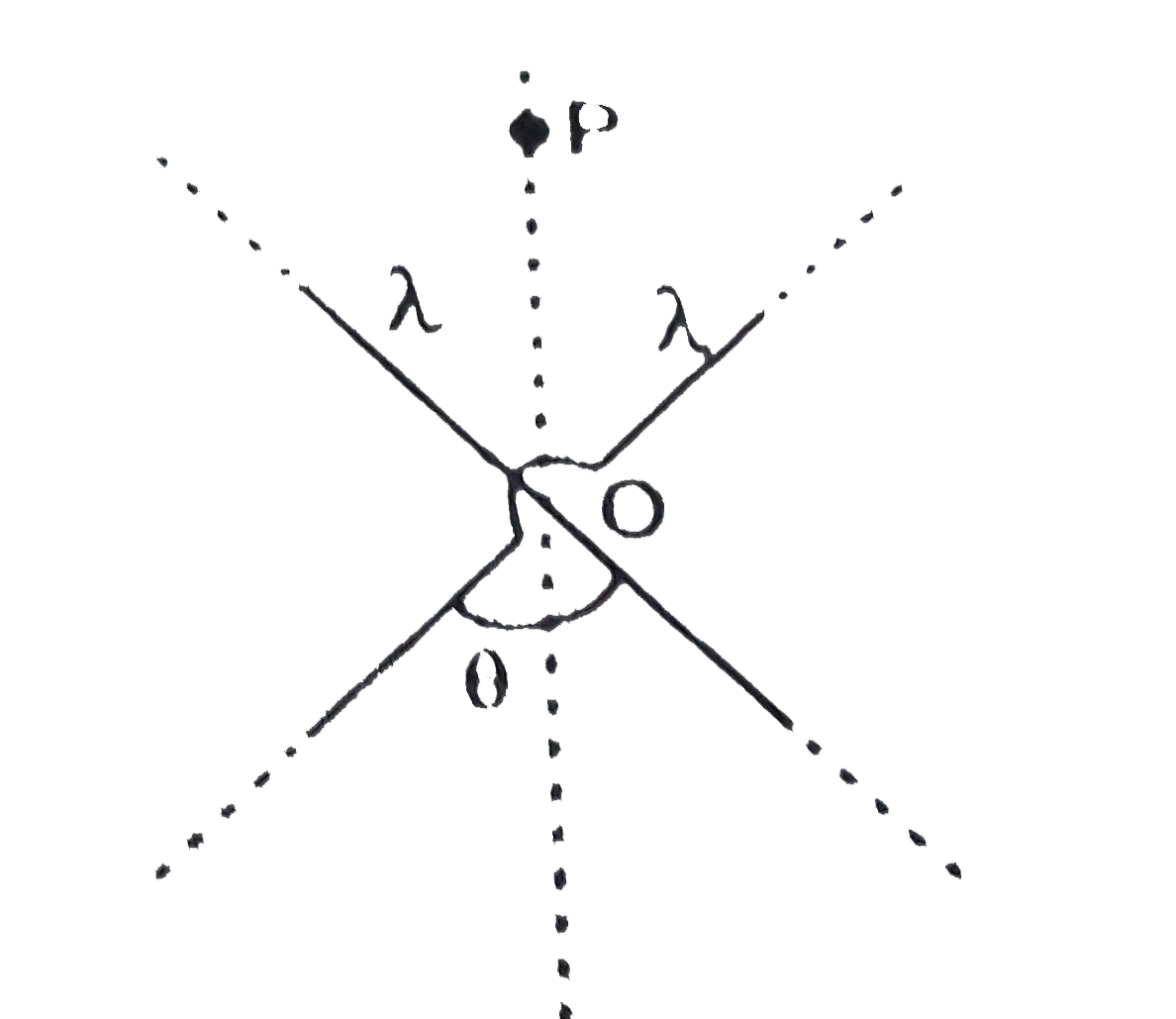
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.

View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
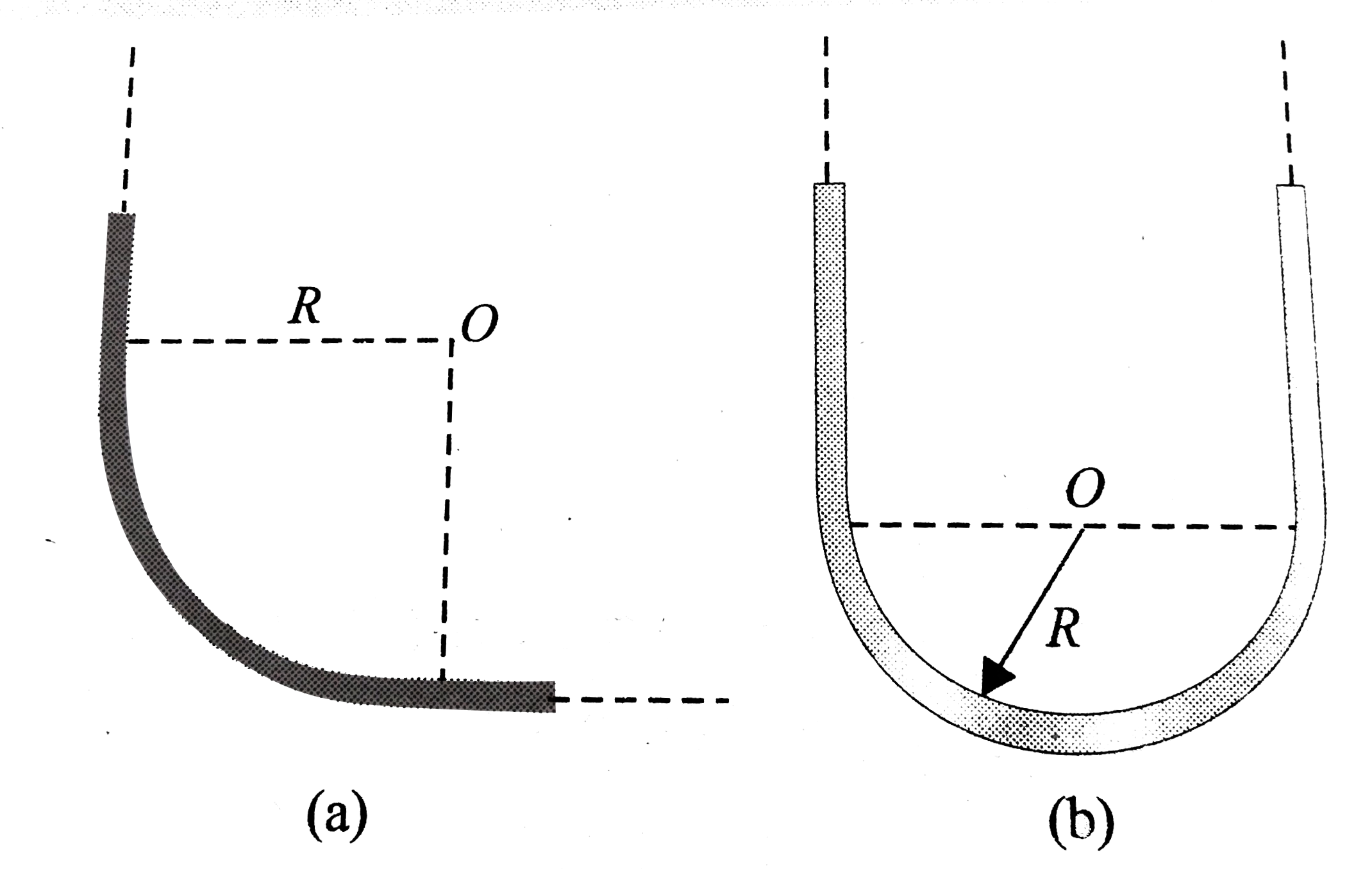
View SolutionTwo mutually perpendicular infinite wires along x -axis and y -axis carry charge densities λ1 and λ2, respectively. The electric line of force at P is along, the line y=1√3x, where P is also a point lying on the same line. Find λ2λ1.
'(##CEN_KSR_PHY_JEE_C18_E01_025_Q12##)'
View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformly charged line charge( linear charge density λ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
View Solution
