In the equation,dN/dt=rN
r' is called the 'intrinsic'rate of natural increase'.
r' is the parameter chosen for assessing impacts of any biotic factor an population growth.
r' is the parameter chosen for assessing impacts abiotic
All of these
The correct Answer is:D
To solve the equation dNdt=rN, we will analyze the components of the equation and understand its implications in the context of population growth.
1. Understanding the Equation:
The equation dNdt=rN represents the rate of change of population size N over time t. Here, r is a constant that represents the intrinsic rate of natural increase of the population.
Hint: Identify what each symbol in the equation represents. N is the population size, t is time, and r is the growth rate.
2. Rearranging the Equation:
We can rearrange the equation to separate the variables:
dNN=rdt
Hint: To solve differential equations, separating variables can simplify the integration process.
3. Integrating Both Sides:
Next, we integrate both sides:
∫dNN=∫rdt
This gives us:
ln|N|=rt+C
where C is the constant of integration.
Hint: Remember that integrating 1N gives ln|N|.
4. Exponentiating to Solve for N:
To solve for N, we exponentiate both sides:
|N|=ert+C
This can be rewritten as:
N=eCert
Let K=eC, then:
N=Kert
Hint: Recognize that K is a constant that can be determined by initial conditions.
5. Interpreting the Result:
The final equation N=Kert indicates that the population grows exponentially over time, where K is the initial population size when t=0.
Hint: The exponential growth model assumes unlimited resources and ideal conditions for growth.
Conclusion:
The equation dNdt=rN describes exponential growth in a population, where r is the intrinsic growth rate. This model is a simplification and assumes constant growth without limiting factors.
The equation dNdt=rN represents the rate of change of population size N over time t. Here, r is a constant that represents the intrinsic rate of natural increase of the population.
We can rearrange the equation to separate the variables:
dNN=rdt
Next, we integrate both sides:
∫dNN=∫rdt
This gives us:
ln|N|=rt+C
where C is the constant of integration.
To solve for N, we exponentiate both sides:
|N|=ert+C
This can be rewritten as:
N=eCert
Let K=eC, then:
N=Kert
The final equation N=Kert indicates that the population grows exponentially over time, where K is the initial population size when t=0.
The equation dNdt=rN describes exponential growth in a population, where r is the intrinsic growth rate. This model is a simplification and assumes constant growth without limiting factors.
Topper's Solved these Questions
Similar Questions
Knowledge Check
which of the following option is true for verhulst Pearl logistic growth?
(A)population growth is decreased by the equation dNdt=rN[KK−N].
(B) r' represents biotic potential.
(C) applicable to a population growing in habitat with limited resources.
(D)K represents carrying capacityAOnly (A)Bonly (B)CA, B and DDB, C and DThe Verhulst-Pearl logistic growth is described to the equation dNdt=rNK−NK, in this K stand
ATemperature in degree KelvinBIntrinsic rate of natural increaseCCarrying capacityDPopulation densityRead the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
The population growth is generally descibed by the following equations :
dN/dt=rN(K−N)/K
What does 'r' represent in the given equation ?APopulation density at time Y.BIntrinsic rate of natural increaseCCarrying capacityDThe base of natural logarithum
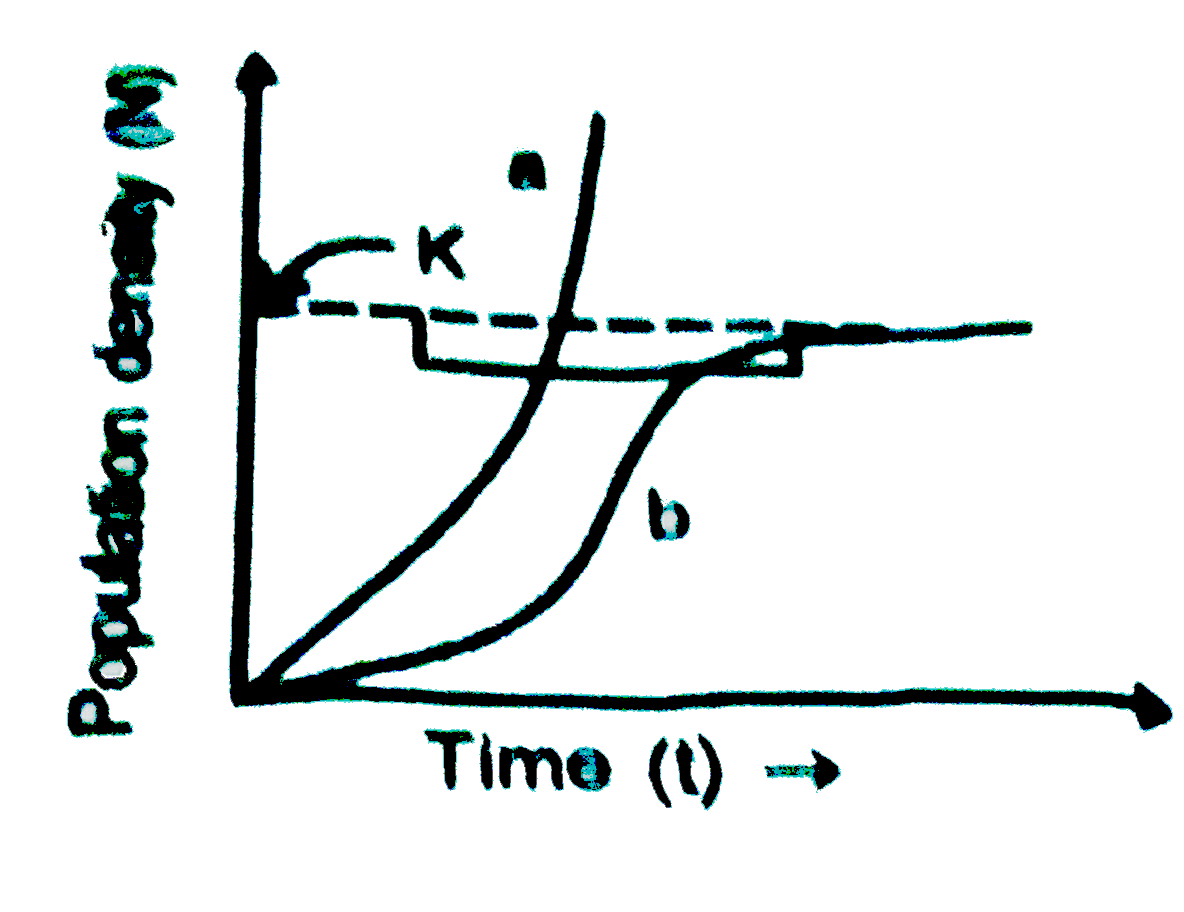
Study the graph given below and answer the questions that follow :
(i) The curve 'b' is described by the following equation :
dNdt=rN{K−NK}
(ii) What does 'K' stand for in this equation ? Mention its significance.
(ii) Which one of the two curves is considered a more realistic one for most of the animal populations ?
(iii) Which curve would depict the population of a species of deer if there are no predators in the habitat ? Why is to so ?
View SolutionThe population growth is generally described by the following equation : dNdt=rN(K−NK) What does 'r' represent in the given equation ?
View SolutionWhen food and space for a population unlimited ?
I. Each species has the ability to realise fully its inherited potential to grow
II. Then it is equal to dN/dt =rN
III. It is described by J-shaped curve
V. Then it has greater intrinsic rate of resources
Vi Then more competition among themselves
Choose the incorrect statements
View SolutionUnder a given condition, it is found that two separate gases effuse out of two separate containers in such a way that they follow the equation dNdt=−K1NanddNdt=−K2NK1=6.93×10−2sec−1.K2=6.93×10−5sec where N is no of molecule remaining in the container.
Which one of the following may represent fraction of number of molecules present after the given interval for gas-I?
View SolutionCarrying capacity in equation dNdt=rN[K−Nk] is :
View Solution
