A particle is moving in a force field given by potential energy U=−λ(x+y+z)from point (1,1,1) to (2, 3, 4). The work done in the process is
3λ
1.5λ
6λ
12λ
The correct Answer is:C
To solve the problem of calculating the work done by a particle moving in a force field defined by the potential energy U=−λ(x+y+z) as it moves from point (1,1,1) to (2,3,4), we can follow these steps:
Step 1: Identify the Initial and Final Points
The initial point is (1,1,1) and the final point is (2,3,4).
Step 2: Calculate the Initial Potential Energy
The potential energy U at the initial point (1,1,1) is calculated as follows:
Uinitial=−λ(1+1+1)=−λ(3)=−3λ
Step 3: Calculate the Final Potential Energy
Next, we calculate the potential energy U at the final point (2,3,4):
Ufinal=−λ(2+3+4)=−λ(9)=−9λ
Step 4: Calculate the Change in Potential Energy
The change in potential energy ΔU is given by:
ΔU=Ufinal−Uinitial=(−9λ)−(−3λ)=−9λ+3λ=−6λ
Step 5: Calculate the Work Done
The work done W by the particle is related to the change in potential energy by the equation:
W=−ΔU
Substituting the value of ΔU:
W=−(−6λ)=6λ
Final Answer
Thus, the work done in the process is:
6λ
The initial point is (1,1,1) and the final point is (2,3,4).
The potential energy U at the initial point (1,1,1) is calculated as follows:
Uinitial=−λ(1+1+1)=−λ(3)=−3λ
Next, we calculate the potential energy U at the final point (2,3,4):
Ufinal=−λ(2+3+4)=−λ(9)=−9λ
The change in potential energy ΔU is given by:
ΔU=Ufinal−Uinitial=(−9λ)−(−3λ)=−9λ+3λ=−6λ
The work done W by the particle is related to the change in potential energy by the equation:
W=−ΔU
Substituting the value of ΔU:
W=−(−6λ)=6λ
Thus, the work done in the process is:
6λ
Topper's Solved these Questions
Similar Questions
A particle is moving from a point (2m,3m) to (1m,1m) under the influence of force with potential energy U=λ(x+y). If work done by the force is nλ, then find the value of n.
View SolutionA particle is moving in a potential region defined by U=K(x2+y2+z2). Calculate the force acting on the particle.
View Solution
Knowledge Check
- Question 1 - Select One
A particle in a certain conservative force field has a potential energy given by U=20xyz. The force exerted on it is
A(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆkB−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆkC−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆkD(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆk - Question 2 - Select One
If the constant due to which it is displaced from a point on a particle due to which it is displaced from a point A(4,−3,−2) to a point B(6,1,−3) then the work done by the forces is
A10 unitsB−10 unitsC−15 unitsD−9 units - Question 3 - Select One or More
A particle is moving in a conservative force field from point A to point B.UA and UB are the potential energies of the particle at point A and B and WC is the work done by conservative forces in the process of taking the particle from A and B, which of the following is true?
AWc=UB−UABWc=UA−UBCUA>UBDUB>UA
A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
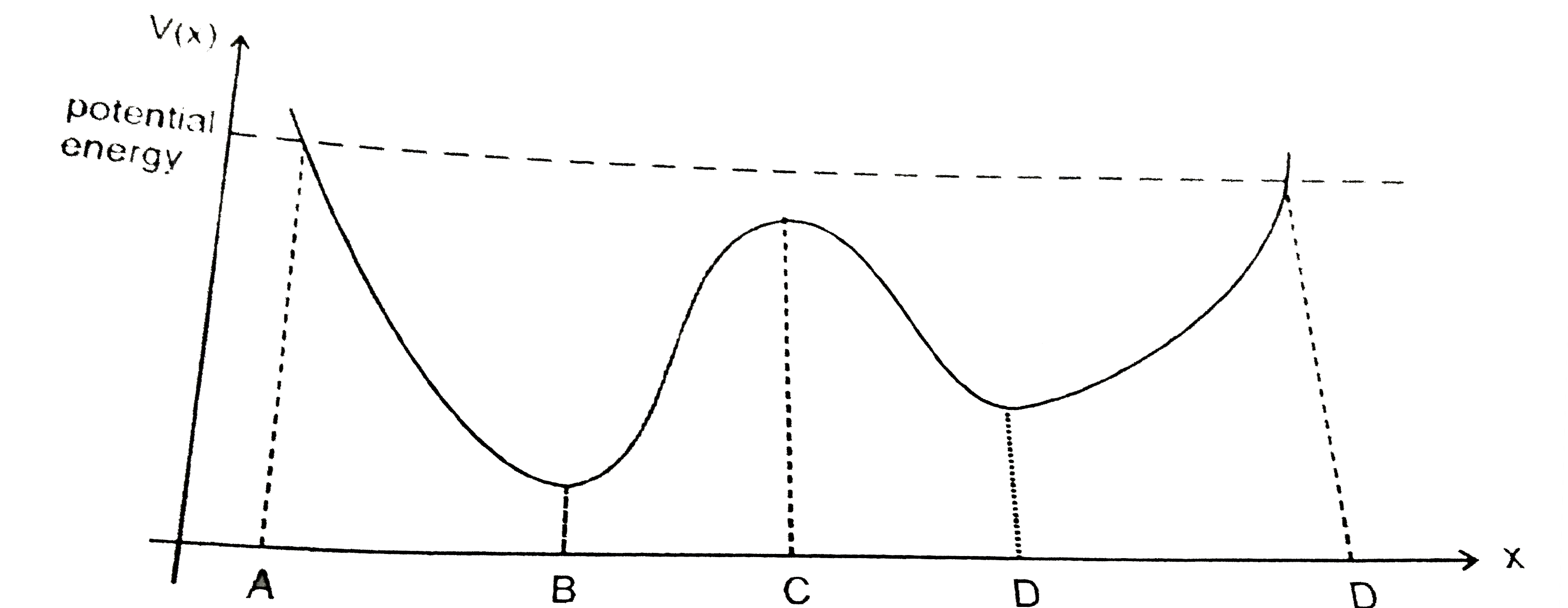
If the particle starts to move from rest from the point A, thenView SolutionA force ¯¯¯F=(3 hati-4 hatj +b hat k)N is acting on the particle which is moving from point A ( 0-1, 1) m to the point B(2, 2 3) m If net work done by the force on the particle is zero then value of b is
View SolutionA particle is moving in a conservative force field from point A to point B.UA and UB are the potential energies of the particle at point A and B and WC is the work done by conservative forces in the process of taking the particle from A and B, which of the following is true?
View SolutionA particle of mass m=3 kg is moving on a straight line in a conservative force field in which the potential energy associated with the particle is given by U(y)=2y2−30y+450. At t=0, particle is at y=8m and moving towards positive y- axis with 1m/s
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The maximum value of potential energy is:View Solution

