A block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
5 N
6 N
5.82 N
4.6 N
The correct Answer is:A
To solve the problem, we need to determine the frictional force acting on the block placed on an accelerating truck. Here’s a step-by-step solution:
Step 1: Identify the Forces Acting on the Block
The block of mass m=1kg is on a truck that accelerates with a=5m/s2. The forces acting on the block include:
- The gravitational force acting downwards, Fg=mg
- The normal force acting upwards, N
- The static frictional force acting to the right (in the direction of the truck's acceleration)
Step 2: Calculate the Gravitational Force
The gravitational force can be calculated using the formula:
Fg=mg
where g≈10m/s2 (acceleration due to gravity). Therefore,
Fg=1kg×10m/s2=10N
Step 3: Determine the Normal Force
Since the block is not moving vertically, the normal force N is equal to the gravitational force:
N=Fg=10N
Step 4: Calculate the Maximum Static Frictional Force
The maximum static frictional force can be calculated using the coefficient of static friction μs:
Ffriction, max=μs⋅N
Given that μs=0.6:
Ffriction, max=0.6×10N=6N
Step 5: Calculate the Pseudo Force
When the truck accelerates, a pseudo force acts on the block in the opposite direction of the truck's acceleration. The pseudo force Fpseudo can be calculated as:
Fpseudo=m⋅a=1kg×5m/s2=5N
Step 6: Compare the Pseudo Force with Maximum Static Friction
The static frictional force will adjust to counteract the pseudo force as long as it does not exceed the maximum static frictional force. Here, the pseudo force 5N is less than the maximum static friction 6N.
Step 7: Conclusion
Since the pseudo force 5N is less than the maximum static friction 6N, the frictional force acting on the block will be equal to the pseudo force:
Ffriction=5N
Thus, the frictional force acting on the block is 5 N.
The block of mass m=1kg is on a truck that accelerates with a=5m/s2. The forces acting on the block include:
- The gravitational force acting downwards, Fg=mg
- The normal force acting upwards, N
- The static frictional force acting to the right (in the direction of the truck's acceleration)
The gravitational force can be calculated using the formula:
Fg=mg
where g≈10m/s2 (acceleration due to gravity). Therefore,
Fg=1kg×10m/s2=10N
Since the block is not moving vertically, the normal force N is equal to the gravitational force:
N=Fg=10N
The maximum static frictional force can be calculated using the coefficient of static friction μs:
Ffriction, max=μs⋅N
Given that μs=0.6:
Ffriction, max=0.6×10N=6N
When the truck accelerates, a pseudo force acts on the block in the opposite direction of the truck's acceleration. The pseudo force Fpseudo can be calculated as:
Fpseudo=m⋅a=1kg×5m/s2=5N
The static frictional force will adjust to counteract the pseudo force as long as it does not exceed the maximum static frictional force. Here, the pseudo force 5N is less than the maximum static friction 6N.
Since the pseudo force 5N is less than the maximum static friction 6N, the frictional force acting on the block will be equal to the pseudo force:
Ffriction=5N
Topper's Solved these Questions
Similar Questions
Knowledge Check
If coefficient of friction between both the block is μ−12 . Find friction force acting between both block.
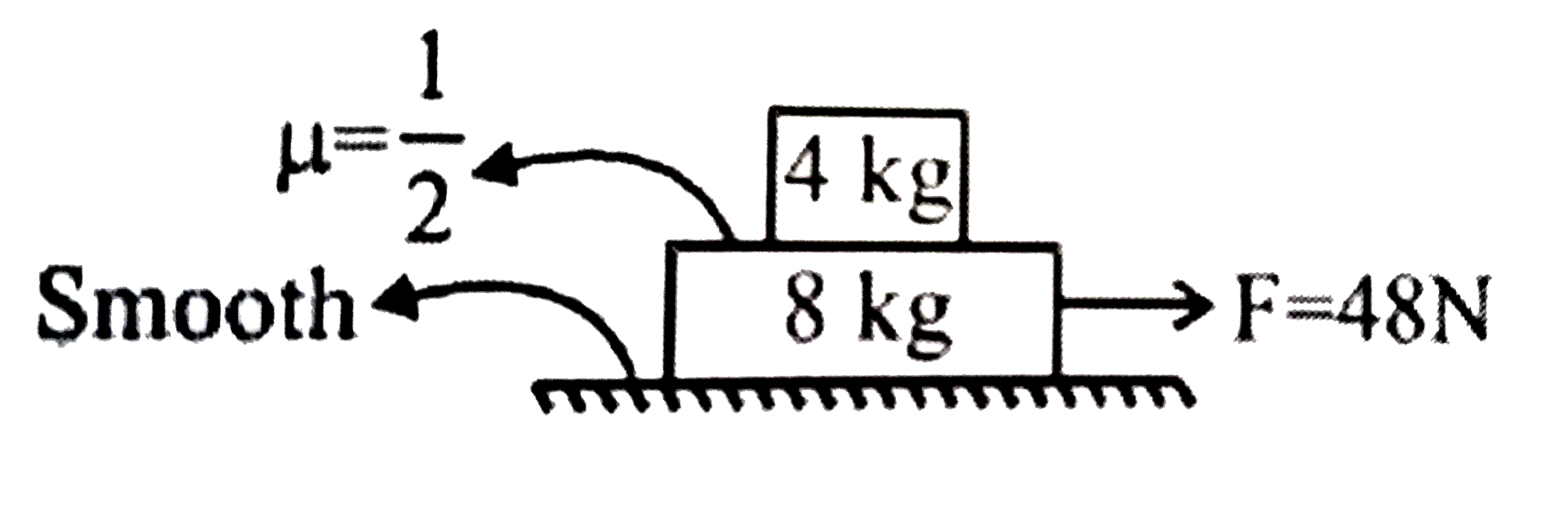 A16NB20NC8ND10N
A16NB20NC8ND10NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8NA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=1m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on theblock is:
A2NB4NC3NDNone of these
The coefficient of static friction between the two blocks is 0.363. What is the acceleration of block 1 so that block 2 does not fall ?

View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA block of mass 6 kg is being pulled by force 24 N as shown . If coefficient of friction between the block and the surface is 0.6 , frictional force acting on the block is :

View SolutionIn the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is

View Solution

