A block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
(a) 1.6
(b) 4.0
(c) 2.0
(d) 2.5
The correct Answer is:C
To find the mass of the block resting on a rough inclined plane, we can use the information provided about the angle of inclination, the coefficient of static friction, and the frictional force acting on the block. Here’s how to solve the problem step by step:
Step 1: Understand the Forces Acting on the Block
The forces acting on the block on the inclined plane include:
1. The gravitational force (weight) acting downwards, which can be resolved into two components:
- Perpendicular to the incline: W_{\perpendicular} = mg \cos(\theta)
- Parallel to the incline: W∥=mgsin(θ)
2. The frictional force acting up the incline, which is given as 10 N.
Step 2: Write the Equation for Frictional Force
The maximum static frictional force can be calculated using the formula:
fs=μsN
where:
- fs is the frictional force (10 N in this case),
- μs is the coefficient of static friction (0.8),
- N is the normal force.
The normal force N can be expressed as:
N=mgcos(θ)
Step 3: Substitute the Normal Force into the Friction Equation
Substituting for N in the frictional force equation gives:
fs=μs(mgcos(θ))
10=0.8(mgcos(30∘))
Step 4: Calculate cos(30∘)
The value of cos(30∘) is:
cos(30∘)=√32
Step 5: Substitute cos(30∘) into the Equation
Now substituting cos(30∘) into the equation:
10=0.8(mg⋅√32)
Step 6: Simplify the Equation
Now simplify the equation:
10=0.4√3mg
Step 7: Solve for Mass m
Rearranging the equation to solve for m:
m=100.4√3g
Using g≈9.8m/s2:
m=100.4√3⋅9.8
Step 8: Calculate the Value of m
Calculating the numerical value:
1. Calculate 0.4√3:
0.4√3≈0.4⋅1.732≈0.6928
2. Now substitute back:
m=100.6928⋅9.8
m≈106.795≈1.47kg
Final Answer
The mass of the block is approximately 1.47 kg.
---
The forces acting on the block on the inclined plane include:
1. The gravitational force (weight) acting downwards, which can be resolved into two components:
- Perpendicular to the incline: W_{\perpendicular} = mg \cos(\theta)
- Parallel to the incline: W∥=mgsin(θ)
2. The frictional force acting up the incline, which is given as 10 N.
The maximum static frictional force can be calculated using the formula:
fs=μsN
where:
- fs is the frictional force (10 N in this case),
- μs is the coefficient of static friction (0.8),
- N is the normal force.
N=mgcos(θ)
Substituting for N in the frictional force equation gives:
fs=μs(mgcos(θ))
10=0.8(mgcos(30∘))
The value of cos(30∘) is:
cos(30∘)=√32
Now substituting cos(30∘) into the equation:
10=0.8(mg⋅√32)
Now simplify the equation:
10=0.4√3mg
Rearranging the equation to solve for m:
m=100.4√3g
Using g≈9.8m/s2:
m=100.4√3⋅9.8
Calculating the numerical value:
1. Calculate 0.4√3:
0.4√3≈0.4⋅1.732≈0.6928
2. Now substitute back:
m=100.6928⋅9.8
m≈106.795≈1.47kg
The mass of the block is approximately 1.47 kg.
Topper's Solved these Questions
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced219videos
HEAT AND THERMODYNAMICS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems1videos
MECHANICAL PROPERTIES OF MATTER AND FLUIDS
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
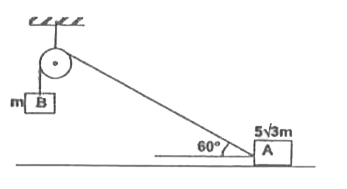
View SolutionA block A of mass 5√4m rests on a rough horizontal plane relative to which its coefficient of friction is μA light string attached to this block passes over a light frictionless pulley and another block B of mass m hangs from it. It is observed that the block A just slips when the string makes an angle of 60∘ with the horizontal .
Find the coefficient of static friction between the block A and the plane. If the same force acting through the sting is applied to the block A in the horizontal direction, find the acceleration of the block A.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
A2 kgB4 kgC1.6 kgD2.5 kg - Question 2 - Select One
A block rests on a rought inclined plane making an angle of 30∘ with horizontal. The coefficient of static friction between the block and inclined plane is 0.8 . If the frictional foerce on the block is 10N, the mass of the block in kg is (g=10m/s2)
A2.0B4.0C1.6D2.5 - Question 3 - Select One
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8N
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block is at rest at the top of a rough inclined plane of inclination 30° with the horizontal. What is the coefficient of kinetic friction between the block and the plane, if the . block slides down with an acceleration of g5 ?
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution

