A mass M is suspended by a rope from a rigid support at A as shown in figure. Another rope is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
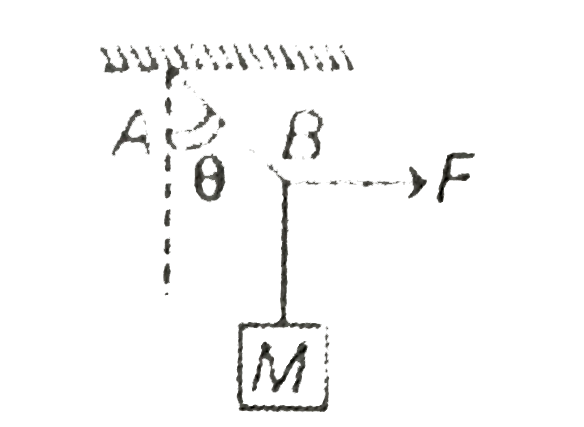
Fsinθ
Fsinθ
Fcosθ
Fcosθ
The correct Answer is:B
Step by step video & image solution for A mass M is suspended by a rope from a rigid support at A as shown in figure. Another rope is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle theta with the vertical in equilibrium then the tension in the string AB is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A mass of 3kg is suspended by a rope of length 2m from the ceilling A force of 40N in the horizontal direction is applied atmidpoint P of the rope the as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling ? (Neglect the mass of the rope, g=10m/s2) .
View SolutionA mass of 3kg is suspended by a rope of length 2m from the ceiling. A force of 40 N in the horizonal direction is applied at midpoint P of the rope as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling? (Neglect the mass of the rope, g=10m/s2)
View Solution
Knowledge Check
A heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
AThe pulse will travel with uniform speedBThe pulse will travel with increasing speedCThe pulse will travel with decreasing speedDThe pulse cannot travel through the ropeA heavy rope is suspended from a rigid support. A wave pulse is set up at the lower end, then
Athe pulse will travel with uniform speedBthe pulse will travel with increasing speedCthe pulse will travel with decreasing speedDthe pulse cannot travel through the ropeA mass of 20 kg is suspended by a rope of length 4 m from the ceiling. A force of 60 N is applied at the midpoint of the rope in the horizontal direction. What is the angle made by the rope with the vertical in equilibrium? Assume that the mass of the rope is negligible and g=10m/s2
Aθ=tan−1(110)Bθ=tan−1(15)Cθ=tan−1(310)Dθ=tan−1(12)
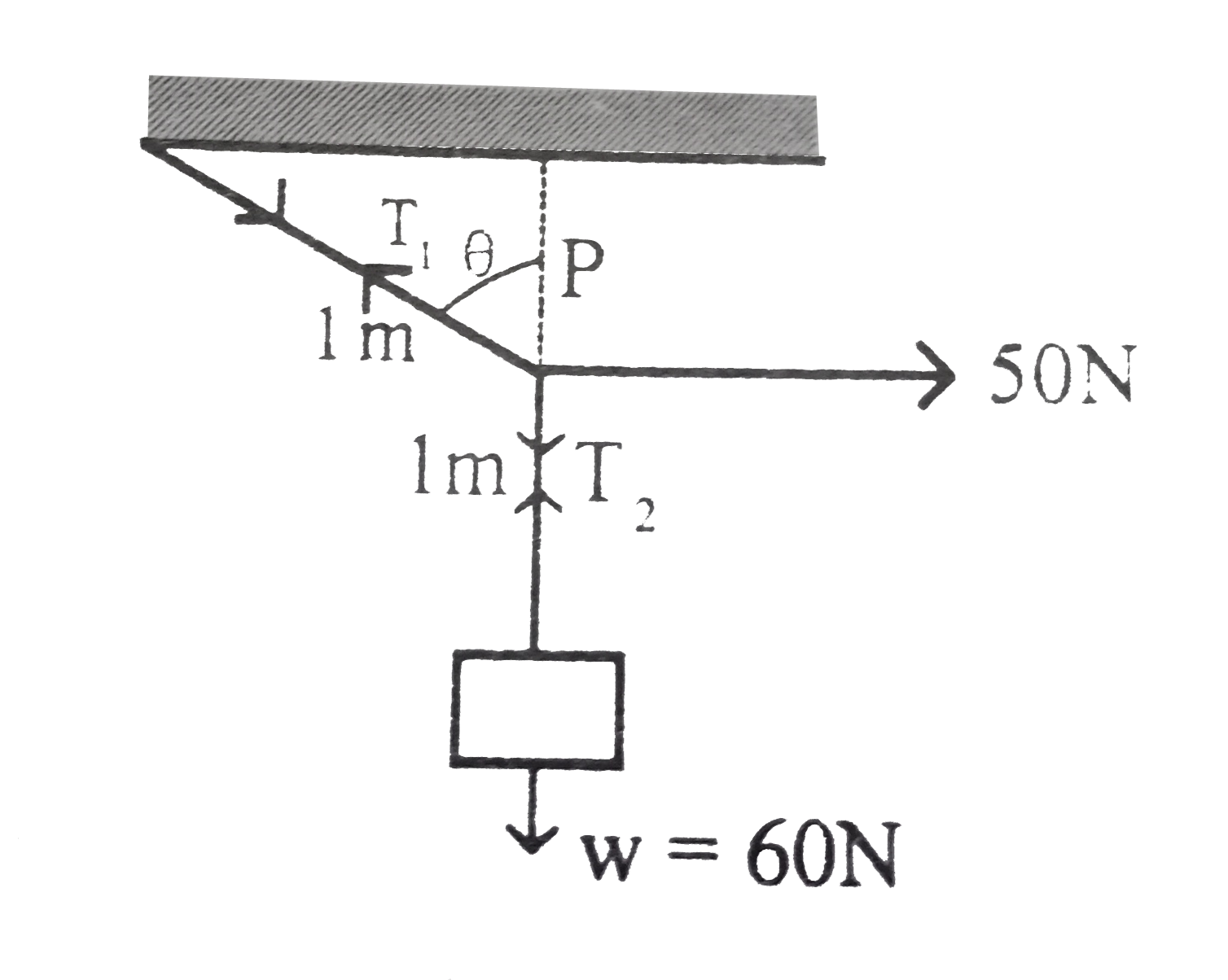
A mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
View SolutionA body of mass √3 kg is suspended by a string to rigid support.The body is pulled horizontally by a force F until the string makes an angle of 30∘ with the vertical.The value of F and tension in the string are
View SolutionA mass of 4kg is suspended by a rope of length 4m from a ceiling. A force of 20N in the horizontal direction is applied at the mid-point of the rope as shown in figure. What is the angle which the rope makes with the vertical in equilibrium? Neglect the mass of the rope. Take g=10ms−2 .
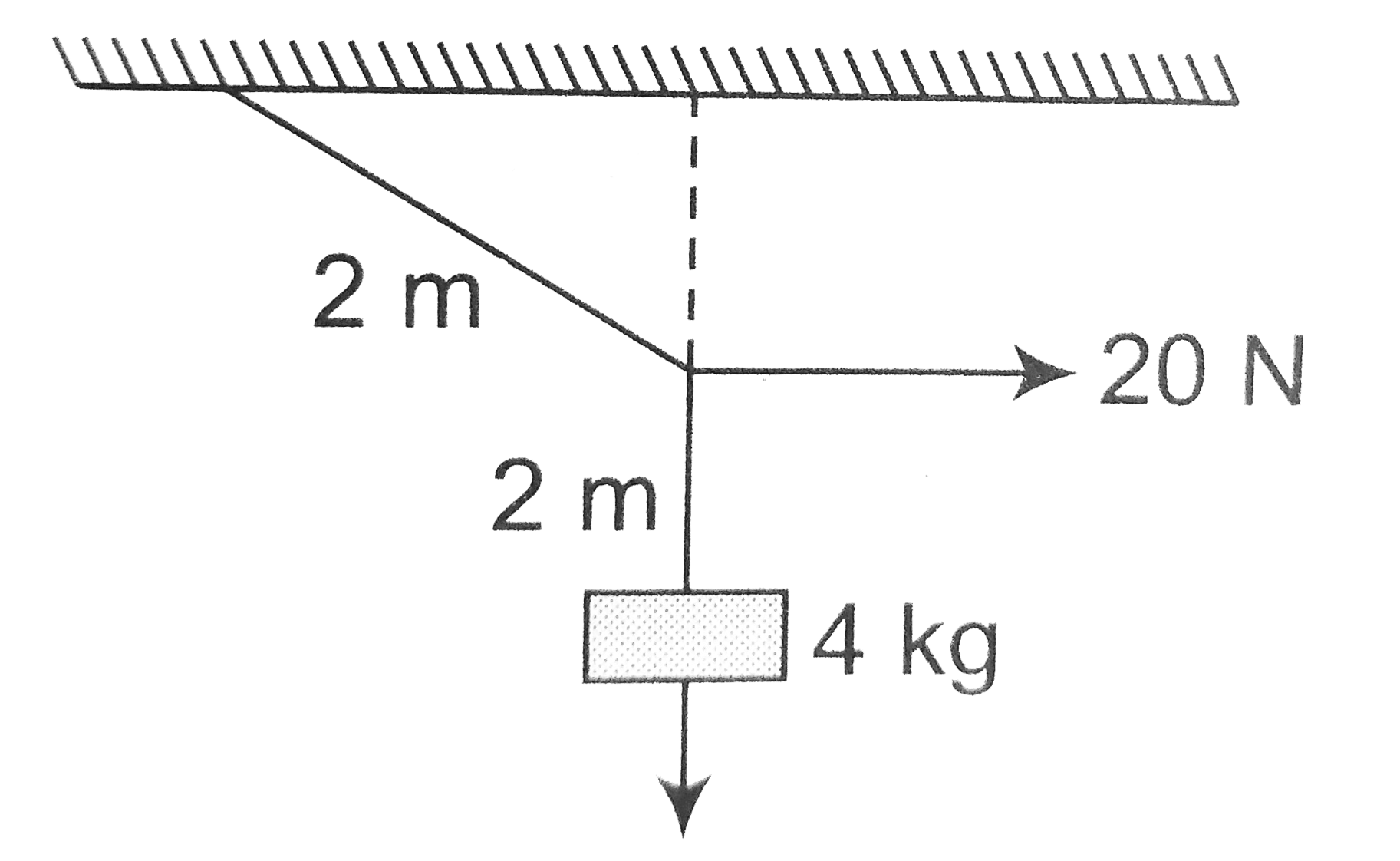
View SolutionA mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
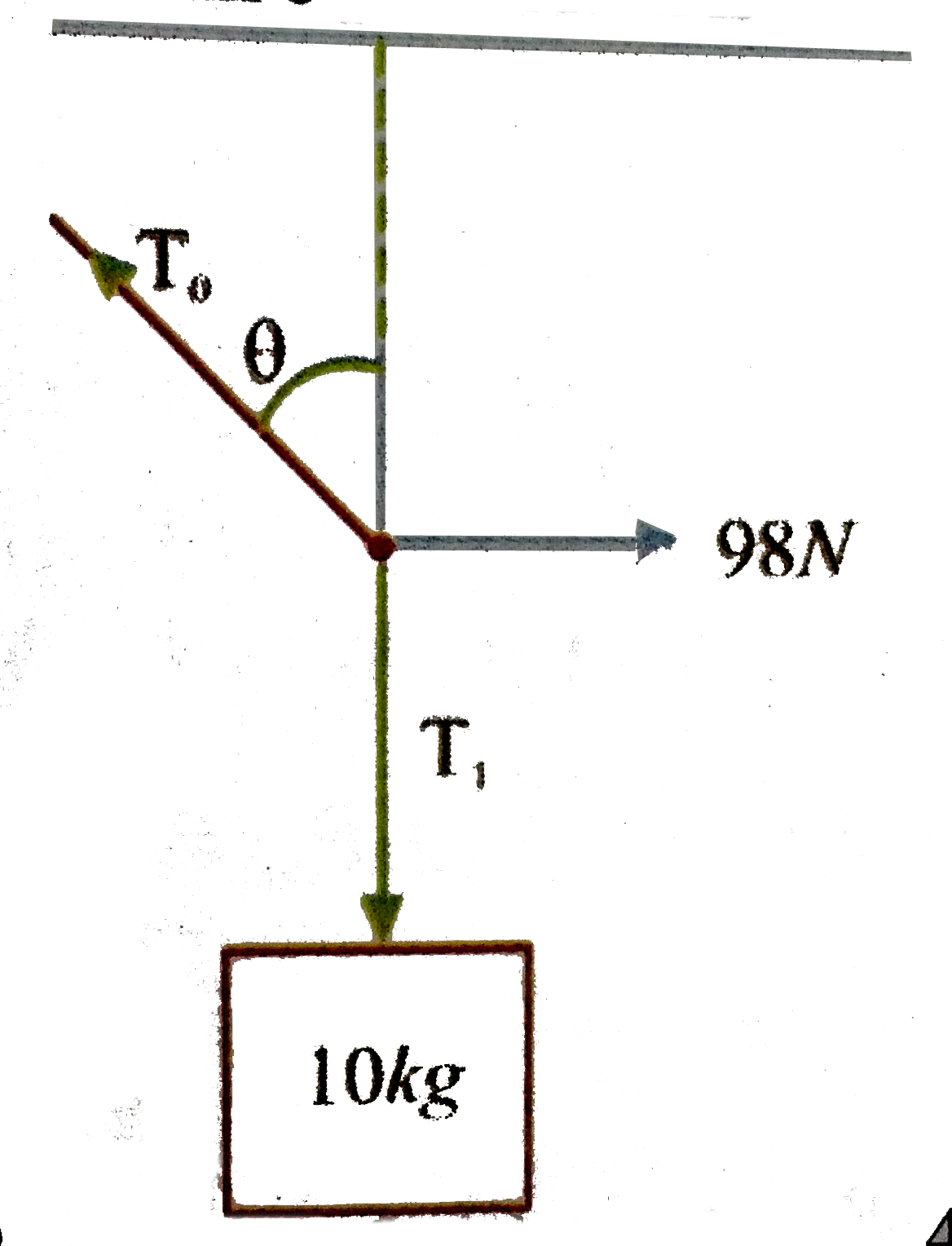
View SolutionA mass of 10kg is suspended by a rope of length 2.8m from a ceiling. A force of 98N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
 .
.
View Solution
