A battery has an open circuit potential difference 10 V between the terminals. When loads 9Ωand4Ω are connected one by one across the battery , the power in the load resistance is the same. The amount of heat approximately generated in one second in the load when a load of 5Ω Is connected across the battery will be
10.4J
9 J
6.8J
4.13J
The correct Answer is:D
To solve the problem step by step, we will follow the outlined concepts and calculations from the video transcript.
Step 1: Understand the given data
- Open circuit potential difference (E) = 10 V
- Load resistances: R1 = 9 Ω and R2 = 4 Ω
- We need to find the heat generated when a load of R = 5 Ω is connected across the battery for a time of T = 1 second.
Step 2: Use the condition of equal power
When the loads R1 and R2 are connected, the power in both loads is the same. The power (P) across a resistor is given by:
P=V⋅I
Where V is the potential difference across the load and I is the current flowing through it.
Using Ohm's law, we can express V as:
V=I⋅R
Thus, the power can also be expressed as:
P=I2⋅R
For the two resistances:
- Power across R1:
P1=I21⋅R1
- Power across R2:
P2=I22⋅R2
Since P1=P2, we have:
I21⋅R1=I22⋅R2
Step 3: Express currents in terms of E and internal resistance
Using the formula for current through a resistor connected to a battery:
I=ER+r
Where r is the internal resistance of the battery.
Thus, we can express:
- I1=ER1+r
- I2=ER2+r
Substituting these into the power equality gives:
(ER1+r)2R1=(ER2+r)2R2
Step 4: Solve for internal resistance (r)
Substituting the values:
(109+r)2⋅9=(104+r)2⋅4
Cross-multiplying and simplifying:
9⋅(4+r)2=4⋅(9+r)2
Expanding both sides:
9(16+8r+r2)=4(81+18r+r2)
144+72r+9r2=324+72r+4r2
Rearranging gives:
5r2−180=0
r2=36
r=6Ω
Step 5: Calculate current (I) for the 5 Ω load
Now we can find the current when a 5 Ω load is connected:
I=ER+r=105+6=1011A
Step 6: Calculate heat generated
Using the formula for heat generated:
H=I2⋅R⋅T
Substituting the values:
H=(1011)2⋅5⋅1
H=100121⋅5
H=500121≈4.13J
Final Answer
The amount of heat generated in one second when a load of 5 Ω is connected across the battery is approximately 4.13 J.
---
- Open circuit potential difference (E) = 10 V
- Load resistances: R1 = 9 Ω and R2 = 4 Ω
- We need to find the heat generated when a load of R = 5 Ω is connected across the battery for a time of T = 1 second.
When the loads R1 and R2 are connected, the power in both loads is the same. The power (P) across a resistor is given by:
P=V⋅I
Where V is the potential difference across the load and I is the current flowing through it.
V=I⋅R
Thus, the power can also be expressed as:
P=I2⋅R
- Power across R1:
P1=I21⋅R1
- Power across R2:
P2=I22⋅R2
I21⋅R1=I22⋅R2
Using the formula for current through a resistor connected to a battery:
I=ER+r
Where r is the internal resistance of the battery.
- I1=ER1+r
- I2=ER2+r
(ER1+r)2R1=(ER2+r)2R2
Substituting the values:
(109+r)2⋅9=(104+r)2⋅4
9⋅(4+r)2=4⋅(9+r)2
9(16+8r+r2)=4(81+18r+r2)
144+72r+9r2=324+72r+4r2
5r2−180=0
r2=36
r=6Ω
Now we can find the current when a 5 Ω load is connected:
I=ER+r=105+6=1011A
Using the formula for heat generated:
H=I2⋅R⋅T
Substituting the values:
H=(1011)2⋅5⋅1
H=100121⋅5
H=500121≈4.13J
The amount of heat generated in one second when a load of 5 Ω is connected across the battery is approximately 4.13 J.
Topper's Solved these Questions
Similar Questions
A battery has an open circuit potential difference of 6V between its terminals. When a load resistance of 60Ω is connected across the battery,the total power supplied by the bttery is 0.4W. What should be the load resistance R, so that maximum power will be dissipated in R. Calculated this power. What is the total power supplied by the battery when such a load is connected?
View SolutionThe potential differnce between the terminals of a battery of emf 6.0 V and internal resistance 1Ω drops to 5.8 V when connected across an external resistor . Find the resistance of the external res
View Solution
Knowledge Check
The potential difference across terminals of cell of 20 V and r=2Ω connected to 8Ω external resistance is
A16B1.6C160D5Two cells having an internal resistance of 0.2Ω and 0.4Ω are connected in parallel, the voltage across the battery is 1.5 V. If the emf of one cell is 1.2 V, then the emf of second cell is
A2.1 VB2.7 VC3 VD4.2 VTwo coils of resistances 3Ωand6Ω are connected in series across a battery of emf12V. Find the electrical energy consumed in 1 minute in each resistance when these are connected in series.
A500 J, 500 JB320 J, 640 JC320 J, 320 JDNone of these
The potential dofference between the terminals of a battery of emf6.0V and internal resistances1(Ω)drops it 5.8 V when connected across an external resistor. Find the resistance of the external resistor.
View SolutionA battery supplies 150W and 196 W power to two resistance of 6Ω and 4Ω when they are connected separately to it. The internal resistance of the battery is:-
View SolutionA 5 V battery with internal resistance 2Ω and a 2V battery with internal resistance 1Ω are connected to a 10Ω as shown in the figure.
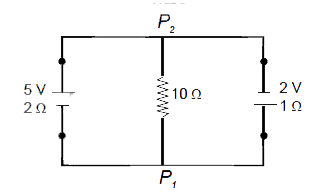
The current in the 10Ω resistance is
View SolutionThe emf of a cell is 2 V. When the terminals of the cell is connected to a resistance 4Ω. The potential difference across the terminals, if internal resistance of cell is 1Ω is
View SolutionFour equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .
View Solution
