A conducting rod of 1 m length and 1 kg mass is suspended by two verticle wires through its ends. An external magnetic field of 2T is applied normal to the rod. Now the current to be passed through the rod so as to make the tension in the wire zero is
[Take g=10ms−2]
15 A
5A
1.5A
2.5A
The correct Answer is:B
To solve the problem, we need to find the current that should be passed through the conducting rod so that the tension in the supporting wires becomes zero. Here's the step-by-step solution:
Step 1: Understand the Forces Acting on the Rod
The rod has two main forces acting on it:
1. The gravitational force (weight) acting downwards, which is given by Fg=mg.
2. The magnetic force acting upwards when current flows through the rod in a magnetic field.
Step 2: Calculate the Weight of the Rod
Given:
- Mass of the rod, m=1kg
- Acceleration due to gravity, g=10m/s2
The weight of the rod can be calculated as:
Fg=mg=1kg×10m/s2=10N
Step 3: Set Up the Equation for Zero Tension
For the tension in the wires to be zero, the magnetic force FB must equal the weight of the rod:
FB=Fg
Thus,
FB=10N
Step 4: Calculate the Magnetic Force
The magnetic force on a current-carrying conductor in a magnetic field is given by the formula:
FB=I⋅L⋅B
Where:
- I is the current in amperes,
- L is the length of the rod (1 m),
- B is the magnetic field strength (2 T).
Substituting the known values into the equation:
FB=I⋅1m⋅2T
FB=2I
Step 5: Set the Magnetic Force Equal to the Weight
Now, we set the magnetic force equal to the weight of the rod:
2I=10N
Step 6: Solve for the Current I
To find I, we rearrange the equation:
I=10N2=5A
Conclusion
The current that needs to be passed through the rod to make the tension in the wires zero is:
5A
The rod has two main forces acting on it:
1. The gravitational force (weight) acting downwards, which is given by Fg=mg.
2. The magnetic force acting upwards when current flows through the rod in a magnetic field.
Given:
- Mass of the rod, m=1kg
- Acceleration due to gravity, g=10m/s2
Fg=mg=1kg×10m/s2=10N
For the tension in the wires to be zero, the magnetic force FB must equal the weight of the rod:
FB=Fg
Thus,
FB=10N
The magnetic force on a current-carrying conductor in a magnetic field is given by the formula:
FB=I⋅L⋅B
Where:
- I is the current in amperes,
- L is the length of the rod (1 m),
- B is the magnetic field strength (2 T).
FB=I⋅1m⋅2T
FB=2I
Now, we set the magnetic force equal to the weight of the rod:
2I=10N
To find I, we rearrange the equation:
I=10N2=5A
The current that needs to be passed through the rod to make the tension in the wires zero is:
5A
Topper's Solved these Questions
Similar Questions
A conducting rod of 1 m length and 1 kg mass is suspended by two vertical wires through its ends. An external magnetic field of 2T is applied normal to the rod. Now, the current to be passed through the rod so as to make the tension in the wires zero is : (Take g=10ms−2) :
View SolutionA straight horizontal conducting rod of length l and mass m is suspended by two vertical wires at its ends. A current I is set up in the rod through the wires.
(i) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero.
(ii) What will be the total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before?
View Solution
Knowledge Check
A straight horizontal conducting rod of length 50 cm and mass 50 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero? (take=10ms−2
A0.05TB0.1TC0.2TD0.5TA straight horizontal conducting rod of length 50 cm and mass 50 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero? (Take g=10 m s−2)
A0.05 TB0.1 TC0.2 TD0.5 TA loop of flexible conducting wire of length l lies in magnetic field B which is normal to the plane of loop. A current l is passed through the loop. The tension developed in the wire to open up is
Aπ2BilBBil2CBil2πDBil
A straight horizontal conducting rod of length 0⋅60m and mass of 60g is suspended by two vertical wires at its ends. A current of 5⋅0A is set up in the rod through the wire. (a) What magnetic field should be set up normal to the conductor in order that the tension in the wire is zero?
(b) What will be total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before (Ignore mass of the wire), g=10ms−2.
View SolutionA straight horizontal conducting rod of length 0⋅45m and mass 60g is suspended by two vertical wires at its end. A current of 5⋅0A is set up in the rod through the wires. (a) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero? (b) What will be the total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before. (Ignore the mass of the wire) g=9⋅8ms−2.
View SolutionA straight horizontal conducting rod of length of 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.
(a) What magnetic field should be set up normal to the conductor in order that the tension in the wire is zero?
(b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires) g=9.8ms−2
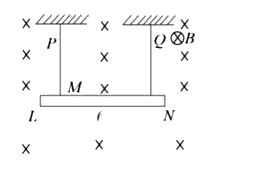
View SolutionA rod of mass M and length l is suspended by two wires P and Q. A uniform magnetic field 'B' is directed into the page. When current through the rod is l. Then the tension in each supporting wire is-
View SolutionA conducting rod of 1m length rotating with a frequency of 50 rev/sec. about its one of end inside the uniform magnetic field of 6.28 mT. The valu of induced emf between end of rod is :-
View Solution
