Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
MR22−M(4R3π)2
MR22−M(√24R3π)2
MR22−M(4R2π)2
MR22−M(√24R3π)2932π
The correct Answer is:B
Step by step video, text & image solution for Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View Solution
Knowledge Check
A uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
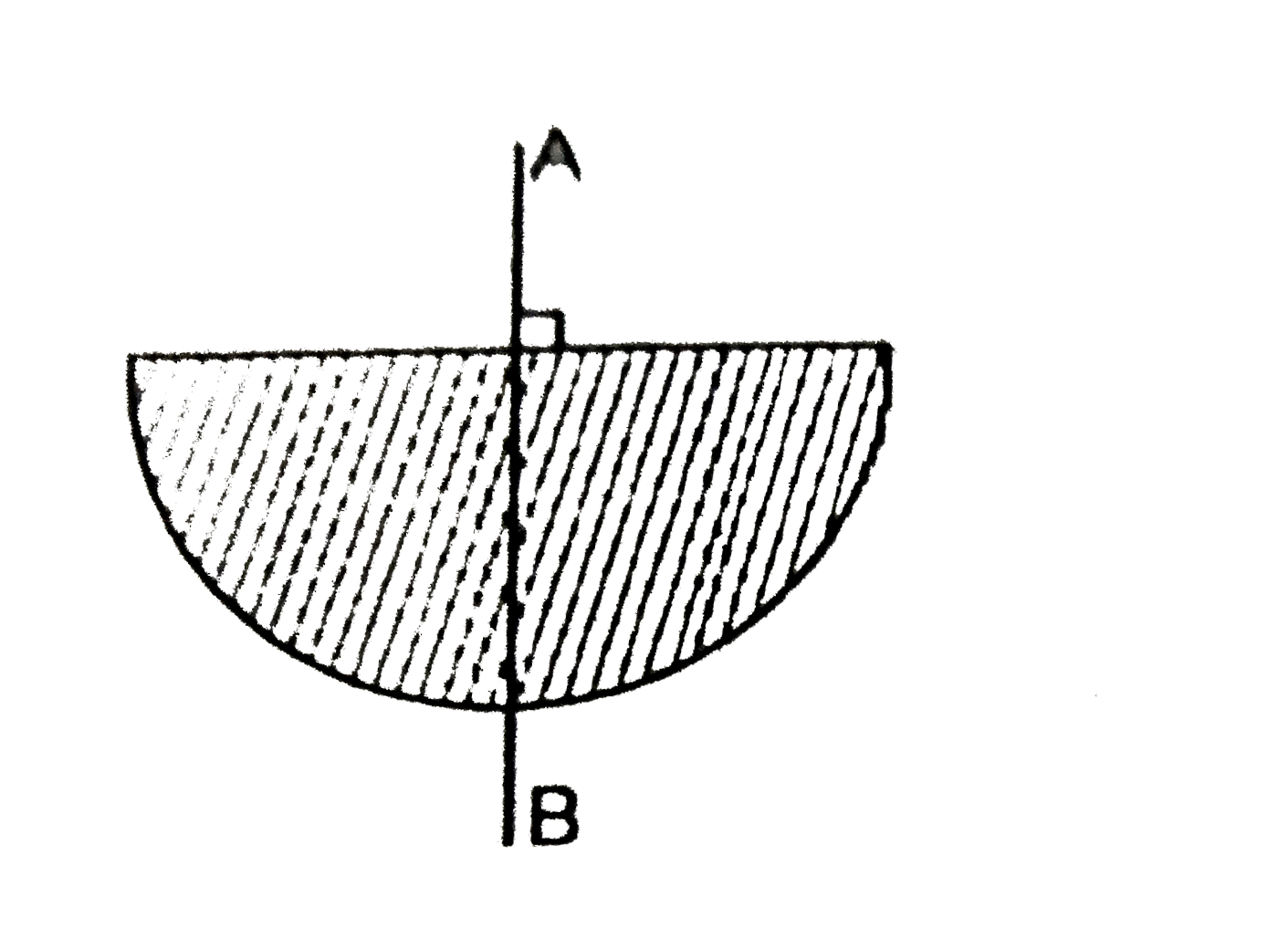 AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2The moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
AML212BMR24CM[L212+R24]DM[L212+R22]Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
ARBR2C√2RDR√2
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionCalculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis through the centre of the disc and perpendicular to its plane
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionFind the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
View SolutionThe moment of inertia of a rod of length l about an axis passing through its centre of mass and perpendicular to rod is I. The moment of inertia of hexagonal shape formed by six such rods, about an axis passing through its centre of mass and perpendicular to its plane will be
View Solution
