In a potentiometer, a uniform potential gradient of 0.8Vm−1 is maintained across its 10 m wire . The potential difference across two points on the wire located at 65 cm and 2.45 m is
1.44 V
0.144 V
1.96 V
0.196 V
The correct Answer is:A
To solve the problem, we need to find the potential difference across two points on a potentiometer wire. Given the potential gradient and the positions of the two points, we can follow these steps:
1. Identify the Given Information:
- Potential gradient (k) = 0.8 V/m
- Length of the wire = 10 m
- Position of the first point (P1) = 65 cm = 0.65 m
- Position of the second point (P2) = 2.45 m
2. Calculate the Length Between the Two Points:
- The length (L) between the two points is calculated as:
L=P2−P1=2.45m−0.65m=1.80m
3. Use the Formula for Potential Difference:
- The potential difference (ΔV) across the two points can be calculated using the formula:
ΔV=k×L
- Substituting the values:
ΔV=0.8V/m×1.80m
4. Calculate the Potential Difference:
- Performing the multiplication:
ΔV=1.44V
5. Conclusion:
- The potential difference across the two points located at 65 cm and 2.45 m is 1.44 V.
- Potential gradient (k) = 0.8 V/m
- Length of the wire = 10 m
- Position of the first point (P1) = 65 cm = 0.65 m
- Position of the second point (P2) = 2.45 m
- The length (L) between the two points is calculated as:
L=P2−P1=2.45m−0.65m=1.80m
- The potential difference (ΔV) across the two points can be calculated using the formula:
ΔV=k×L
- Substituting the values:
ΔV=0.8V/m×1.80m
- Performing the multiplication:
ΔV=1.44V
- The potential difference across the two points located at 65 cm and 2.45 m is 1.44 V.
Topper's Solved these Questions
Similar Questions
The potential gradient along the length of uniform wire is 10 Vm−1. The length of the wire is 1 m. What is the potential difference across two points on the wire separated by 25 cm?
View SolutionIn the circuit shown, a potential difference of 60 V is applied across AB. The potential difference between the points M and N is
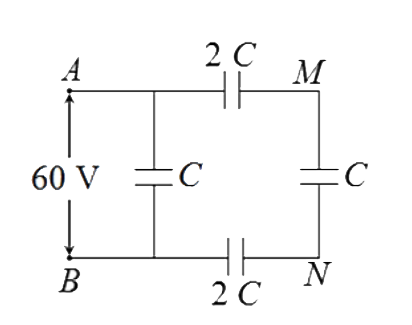
View Solution
Knowledge Check
In the circuit shown, a potential difference of 60V is applied across AB. The potential difference between the point M and N is
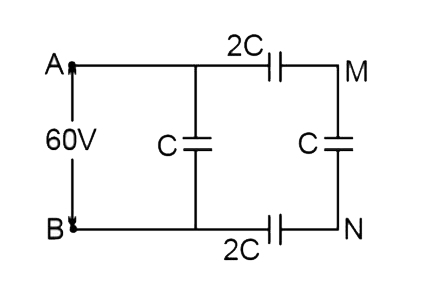 A10 VB15 VC20 VD30 V
A10 VB15 VC20 VD30 VIn a potentiometer, potential difference across the potentiometer wire is directly proportional to its
ALengthBareaCresistanceDall of theseA potentiometer has uniform potential gradient across it. Two cells connected in series (i) to support each other and (ii) to oppose each other are balanced over 6 m and 2 m respectively on the potentiometer wire. The e.m.f.’s of the cells are in the ratio of
A1:2B1:1C3:1D2:1
A potentiometer consists of a wire of length 4 m and resistance 10Ω. If is connected of cell of emf 2V. The potential difference per unit length of the wire will be
View SolutionA potentiometer has uniform potential gradient. The specific resistance of the material of the potentiometer wire is 10−7 ohm-metre and the current passing through it is 0.1 ampere, cross-section of the wire is 10−6 m2. The potential gradient along the potentiometer wire is
View SolutionA potentiometer wire of length 400 cm has a resistance of 8Ω. If a potential gradient of 0.5 V/m is maintained throughout the length of the wire, then the current flowing through the wire is
View SolutionA potentiometer wire is 500 cm long and potential difference of 4 V is maintained between the ends of the wire. The e.m.f. of the cell which balances against the length of 135 cm of the wire is
View SolutionA current of 2amp is flowing in the primary circuit of a potentiometer wire having resistance of 0.2ohm/m. In a coil when current of 1A flows, then potential difference across its terminals are balanced at 2.5m of the potentiometer wire. The resistance of the coil is
View Solution
