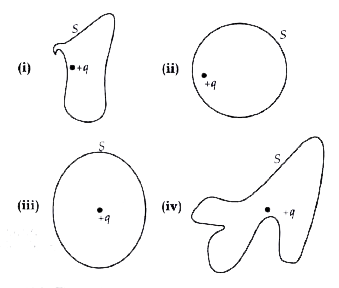If the magnetic field is parallel to a surface then, the magnetic flux through the surface is
zero
small but not zero
infinite
large but not infinite
The correct Answer is:A
To solve the problem, we need to understand the concept of magnetic flux and how it relates to the orientation of the magnetic field with respect to a surface.
1. Understanding Magnetic Flux:
Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) of the surface, taking into account the angle (θ) between the magnetic field and the normal (perpendicular) to the surface. The formula for magnetic flux is given by:
Φ=B⋅A⋅cos(θ)
2. Identifying the Angle:
In this scenario, the magnetic field is parallel to the surface. This means that the angle (θ) between the magnetic field and the normal to the surface is 90 degrees (90°).
3. Calculating the Cosine of the Angle:
We know that:
cos(90°)=0
4. Substituting Values into the Flux Formula:
Now, substituting the angle into the magnetic flux formula:
Φ=B⋅A⋅cos(90°)=B⋅A⋅0
5. Conclusion:
Therefore, the magnetic flux through the surface is:
Φ=0
Final Answer:
If the magnetic field is parallel to a surface, then the magnetic flux through the surface is 0.
---
Magnetic flux (Φ) through a surface is defined as the product of the magnetic field (B) and the area (A) of the surface, taking into account the angle (θ) between the magnetic field and the normal (perpendicular) to the surface. The formula for magnetic flux is given by:
Φ=B⋅A⋅cos(θ)
In this scenario, the magnetic field is parallel to the surface. This means that the angle (θ) between the magnetic field and the normal to the surface is 90 degrees (90°).
We know that:
cos(90°)=0
Now, substituting the angle into the magnetic flux formula:
Φ=B⋅A⋅cos(90°)=B⋅A⋅0
Therefore, the magnetic flux through the surface is:
Φ=0
If the magnetic field is parallel to a surface, then the magnetic flux through the surface is 0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The electric flux through the surface
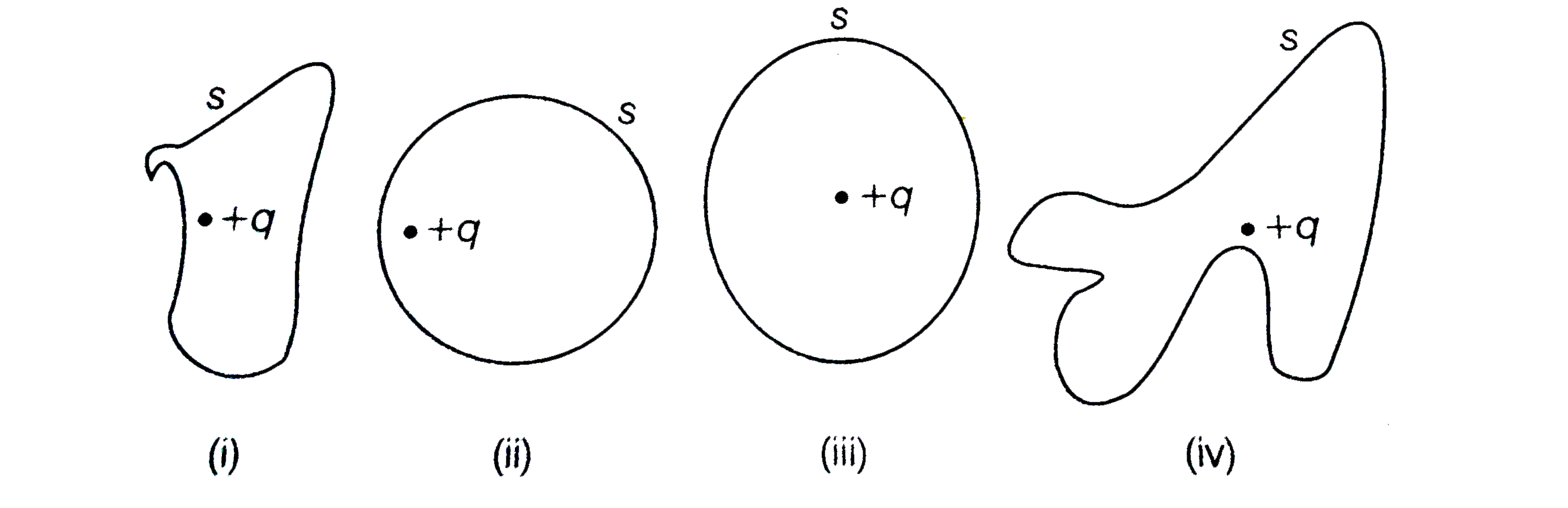 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures. - Question 2 - Select One
The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures. - Question 3 - Select One
The black shapes in the figure below are closed surfaces. The electric field lines are in red. For which case the net flux through the surfaces is non-zero ?
 AIn all cases net flux is non-zeroBOnly (c) and (d)COnly (a) and (b)DOnly (b), (c) and (d)
AIn all cases net flux is non-zeroBOnly (c) and (d)COnly (a) and (b)DOnly (b), (c) and (d)
When a 10 μC charge is enclosed by a closed surface, the flux passing through the surface is ϕ. Now another 10 µC charge is placed inside the closed surface, then the flux passing through the surface is ______.
View SolutionA surface enclosed an electric dipole, the flux through the surface is -
View SolutionAssertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity ω as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field.
Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.
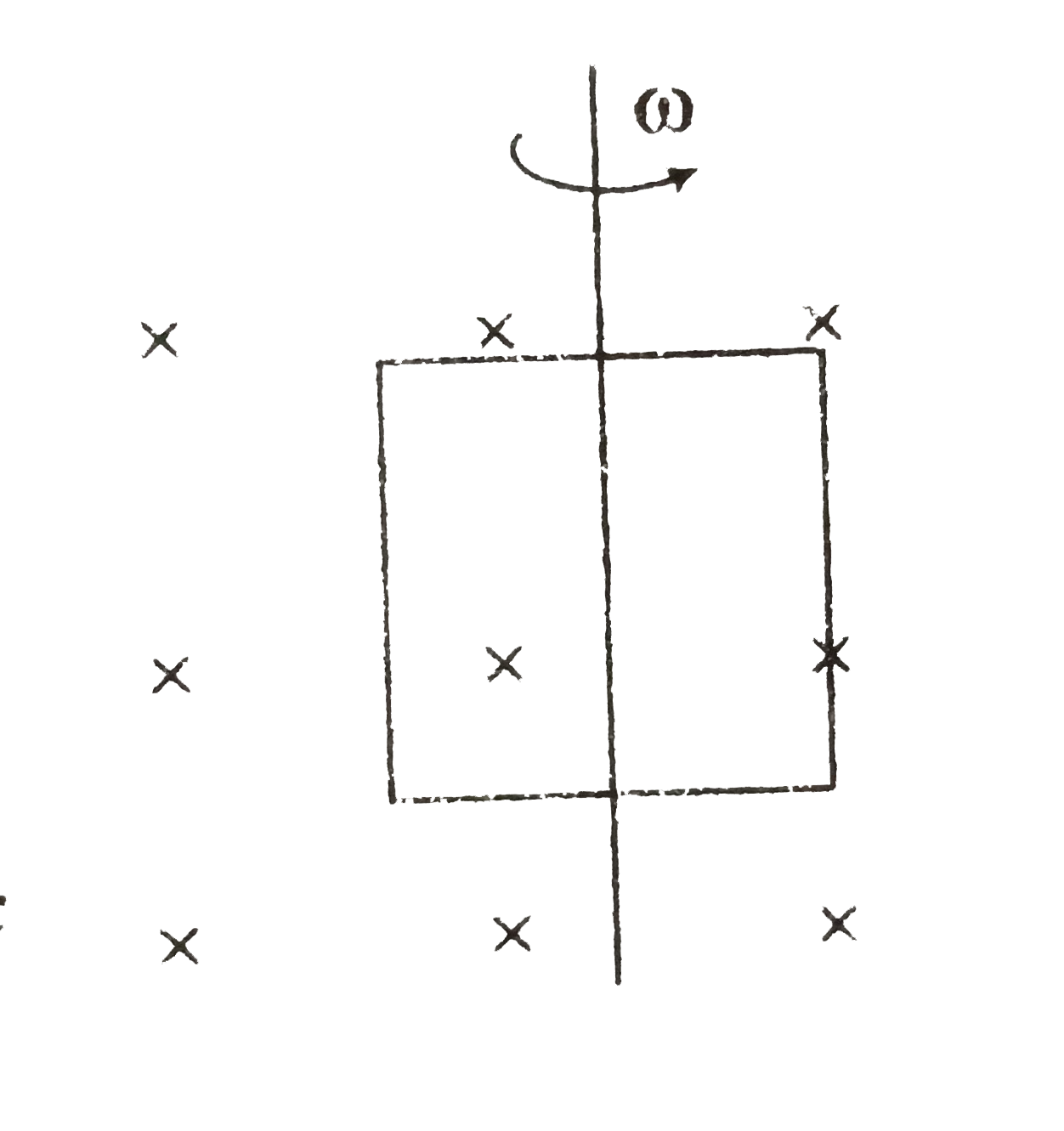 View Solution
View SolutionA hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
View SolutionA hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
View Solution