Which of the following graphs correctly represents the relation between In (E) and In (T), where E is the amount of radiation emitted per unit time from a unit area of the body and T is the absolute temperature ?
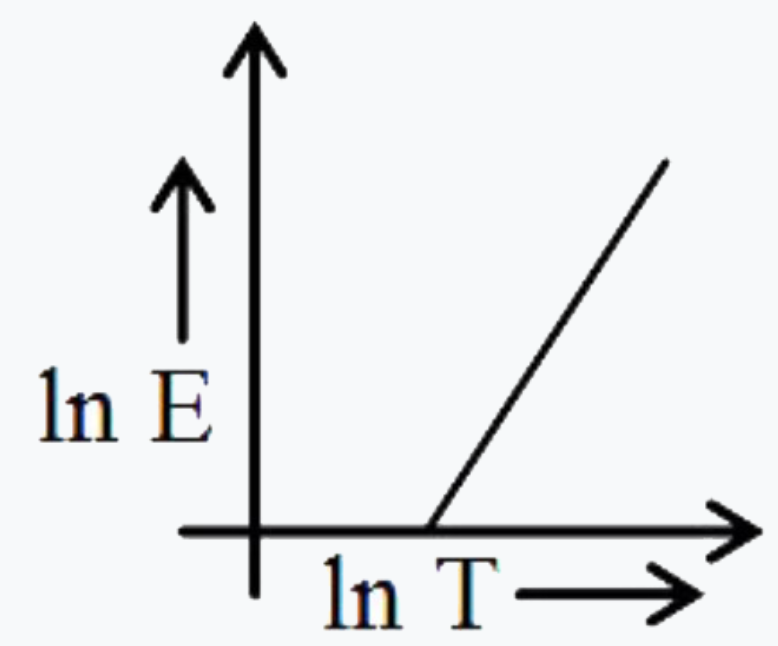

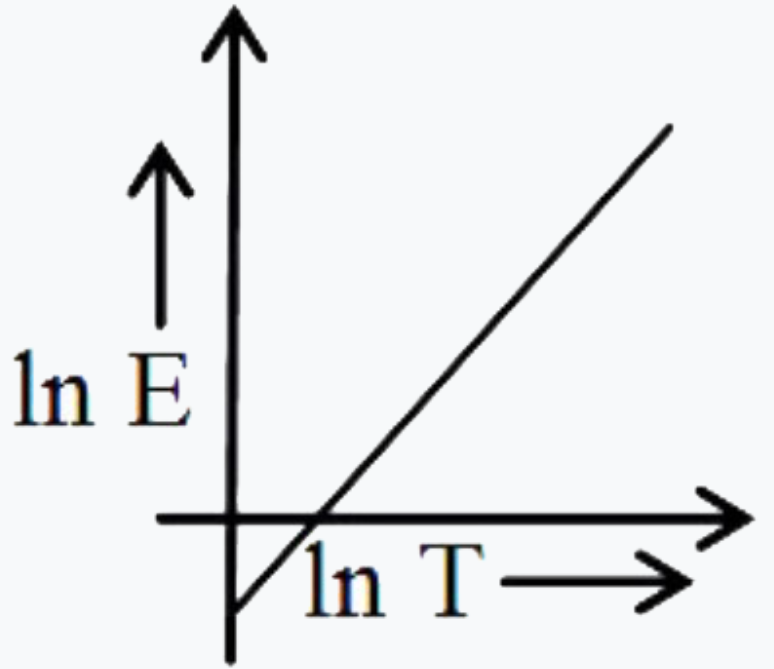
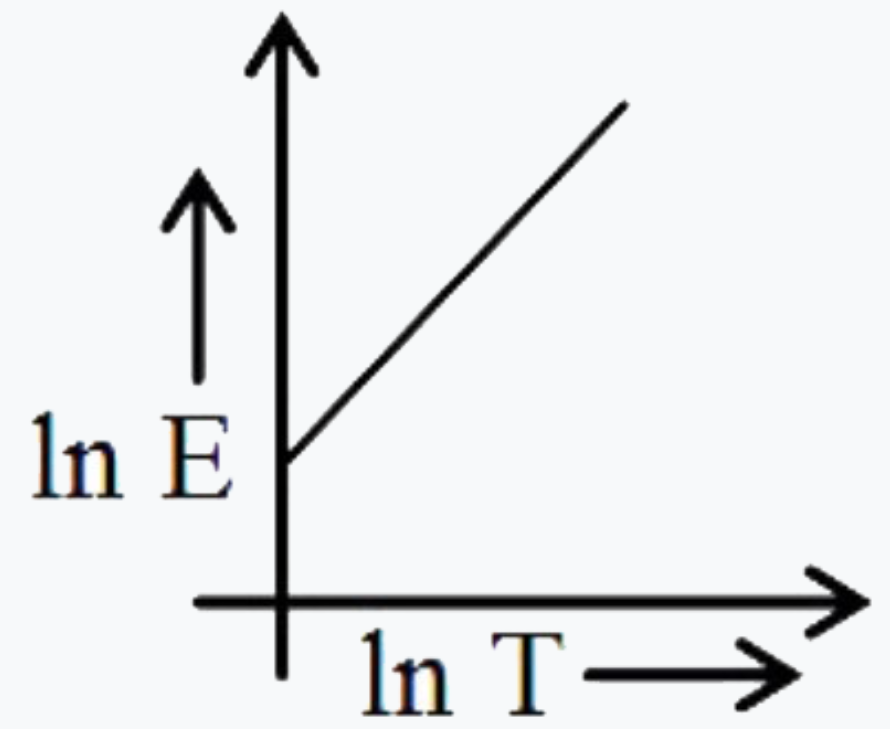
The correct Answer is:C
To determine the correct graph representing the relationship between ln(E) and ln(T), where E is the amount of radiation emitted per unit time from a unit area of the body and T is the absolute temperature, we can follow these steps:
Step 1: Understand Stefan-Boltzmann Law
According to the Stefan-Boltzmann law, the amount of radiation emitted per unit area E is proportional to the fourth power of the absolute temperature T:
E=σT4
where σ is the Stefan-Boltzmann constant.
Step 2: Take the Natural Logarithm
To find the relationship between ln(E) and ln(T), we take the natural logarithm of both sides of the equation:
ln(E)=ln(σT4)
Step 3: Apply Logarithmic Properties
Using the properties of logarithms, we can expand the right-hand side:
ln(E)=ln(σ)+ln(T4)
ln(E)=ln(σ)+4ln(T)
Step 4: Rearrange the Equation
We can rearrange the equation to express it in the form of y=mx+c:
ln(E)=4ln(T)+ln(σ)
This indicates that ln(E) is a linear function of ln(T) with a slope of 4 and a y-intercept of ln(σ).
Step 5: Analyze the Graph
Since σ (the Stefan-Boltzmann constant) is a positive constant, ln(σ) will be a negative value (as σ<1). Therefore, the y-intercept of the graph will be negative. The slope of 4 indicates that for every unit increase in ln(T), ln(E) increases by 4 units.
Step 6: Conclusion
The graph that correctly represents this relationship will have a positive slope (indicating that as T increases, E also increases) and a negative y-intercept (since ln(σ)<0).
Thus, the correct graph is option C.
According to the Stefan-Boltzmann law, the amount of radiation emitted per unit area E is proportional to the fourth power of the absolute temperature T:
E=σT4
where σ is the Stefan-Boltzmann constant.
To find the relationship between ln(E) and ln(T), we take the natural logarithm of both sides of the equation:
ln(E)=ln(σT4)
Using the properties of logarithms, we can expand the right-hand side:
ln(E)=ln(σ)+ln(T4)
ln(E)=ln(σ)+4ln(T)
We can rearrange the equation to express it in the form of y=mx+c:
ln(E)=4ln(T)+ln(σ)
This indicates that ln(E) is a linear function of ln(T) with a slope of 4 and a y-intercept of ln(σ).
Since σ (the Stefan-Boltzmann constant) is a positive constant, ln(σ) will be a negative value (as σ<1). Therefore, the y-intercept of the graph will be negative. The slope of 4 indicates that for every unit increase in ln(T), ln(E) increases by 4 units.
The graph that correctly represents this relationship will have a positive slope (indicating that as T increases, E also increases) and a negative y-intercept (since ln(σ)<0).
Topper's Solved these Questions
Similar Questions
Knowledge Check
The amount of heat enerrgy radiated per unit time per unit area by a body depends upon
Aarea of the bodyBtemperature and nature of the bodyCnature of the body onlyDall of theseWhich one of the following correctly represents the variation between linear momentum (P) and kinetic energy (E) ofa body?
A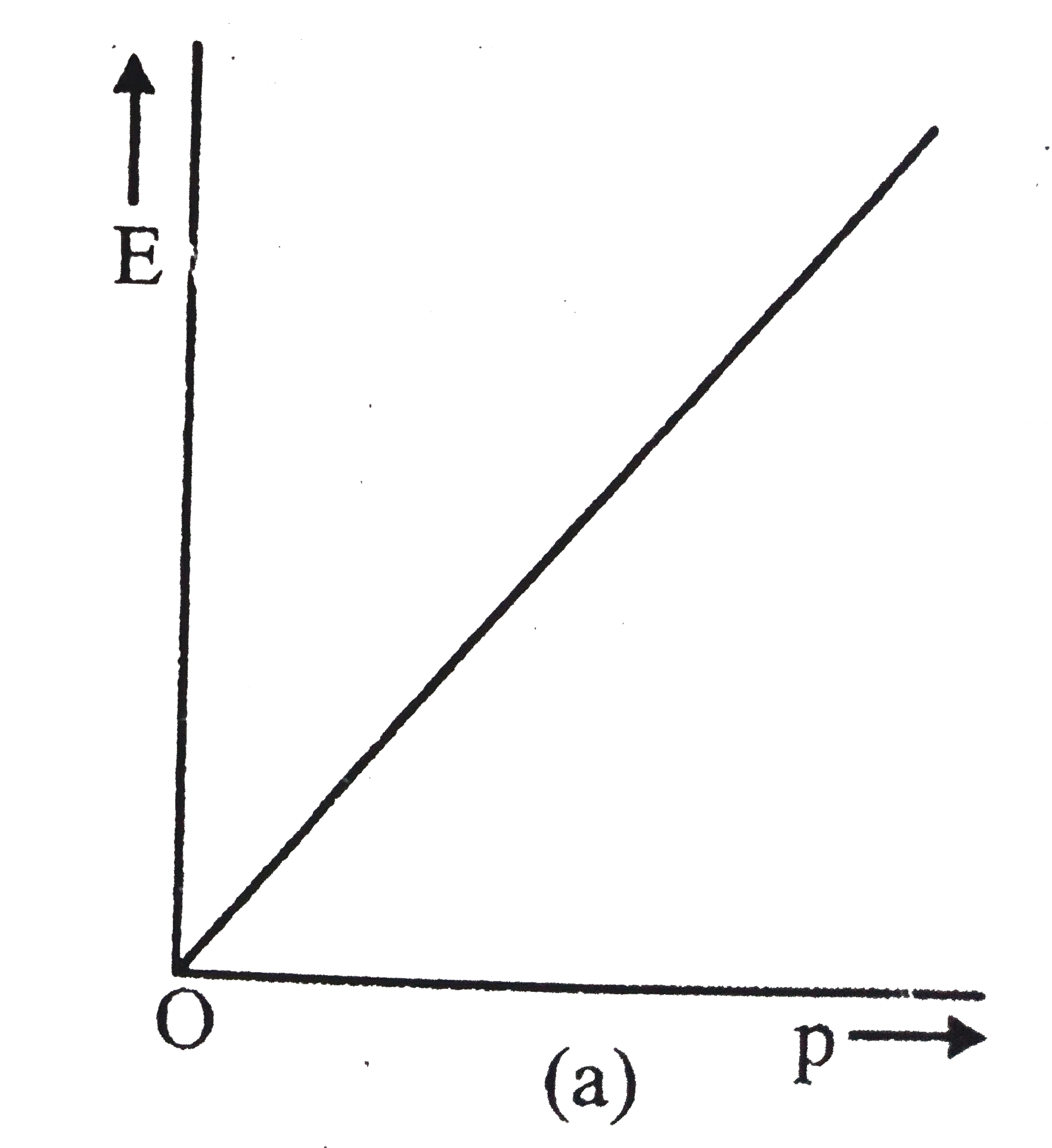 B
B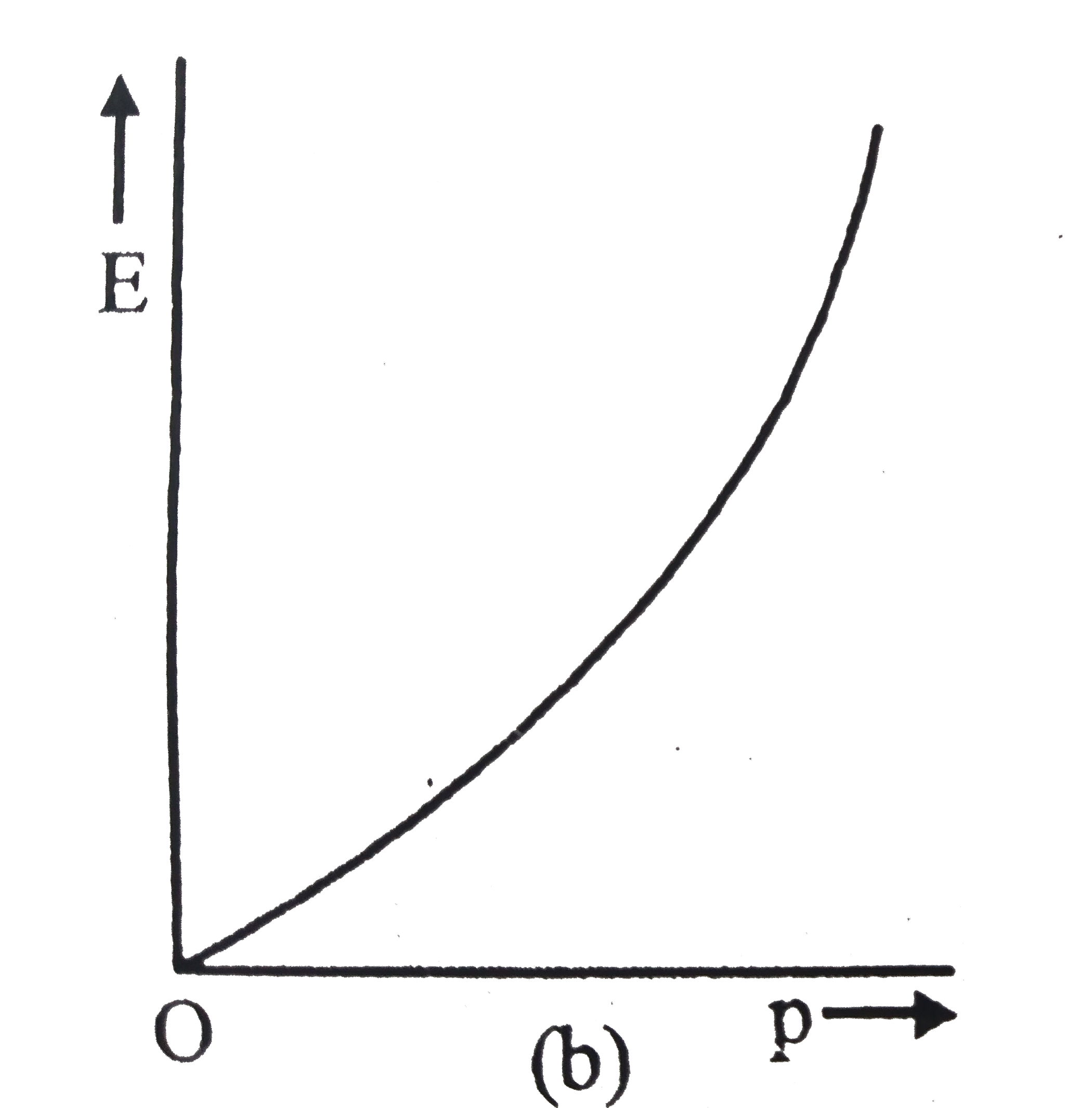 C
C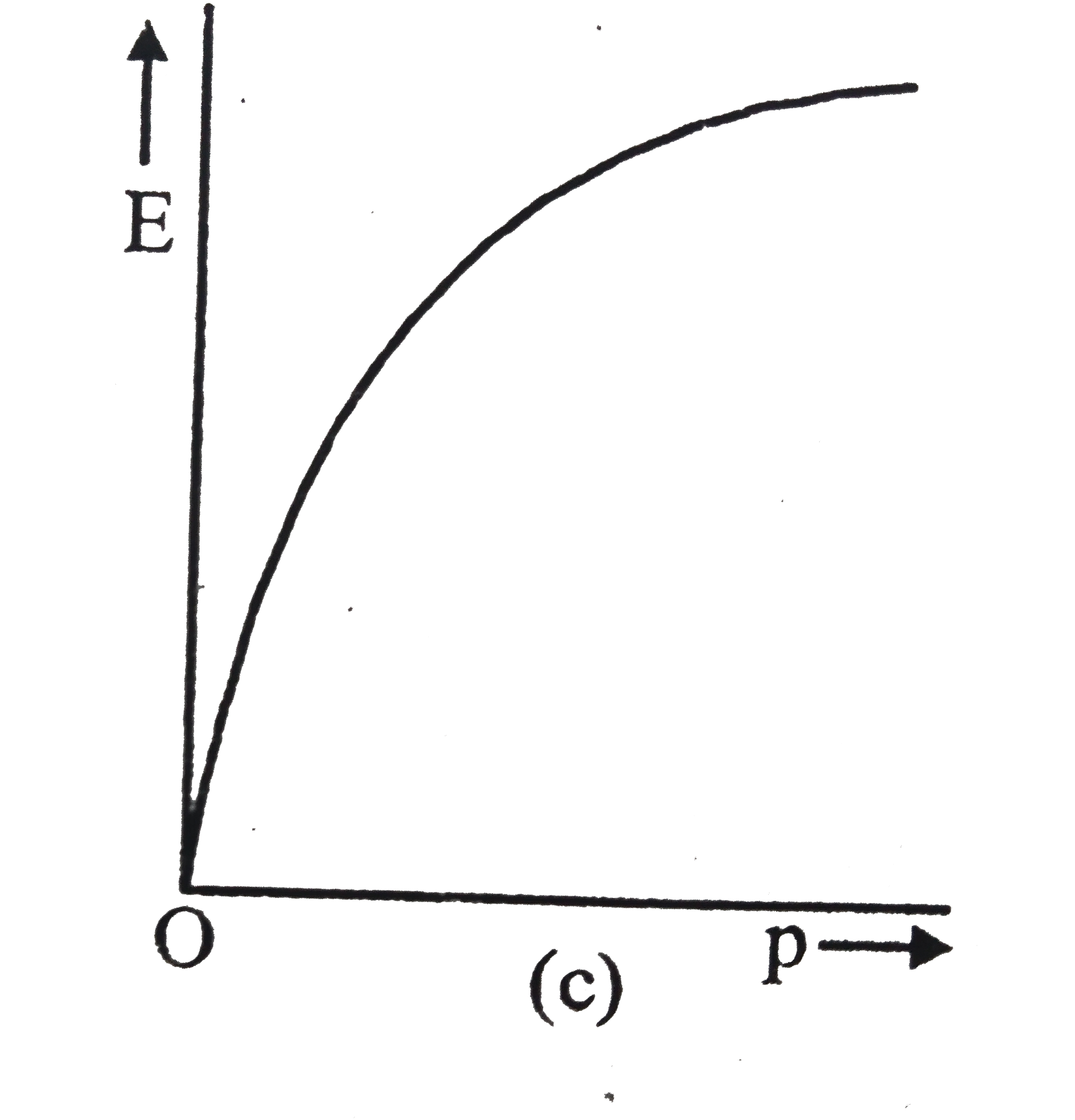 D
D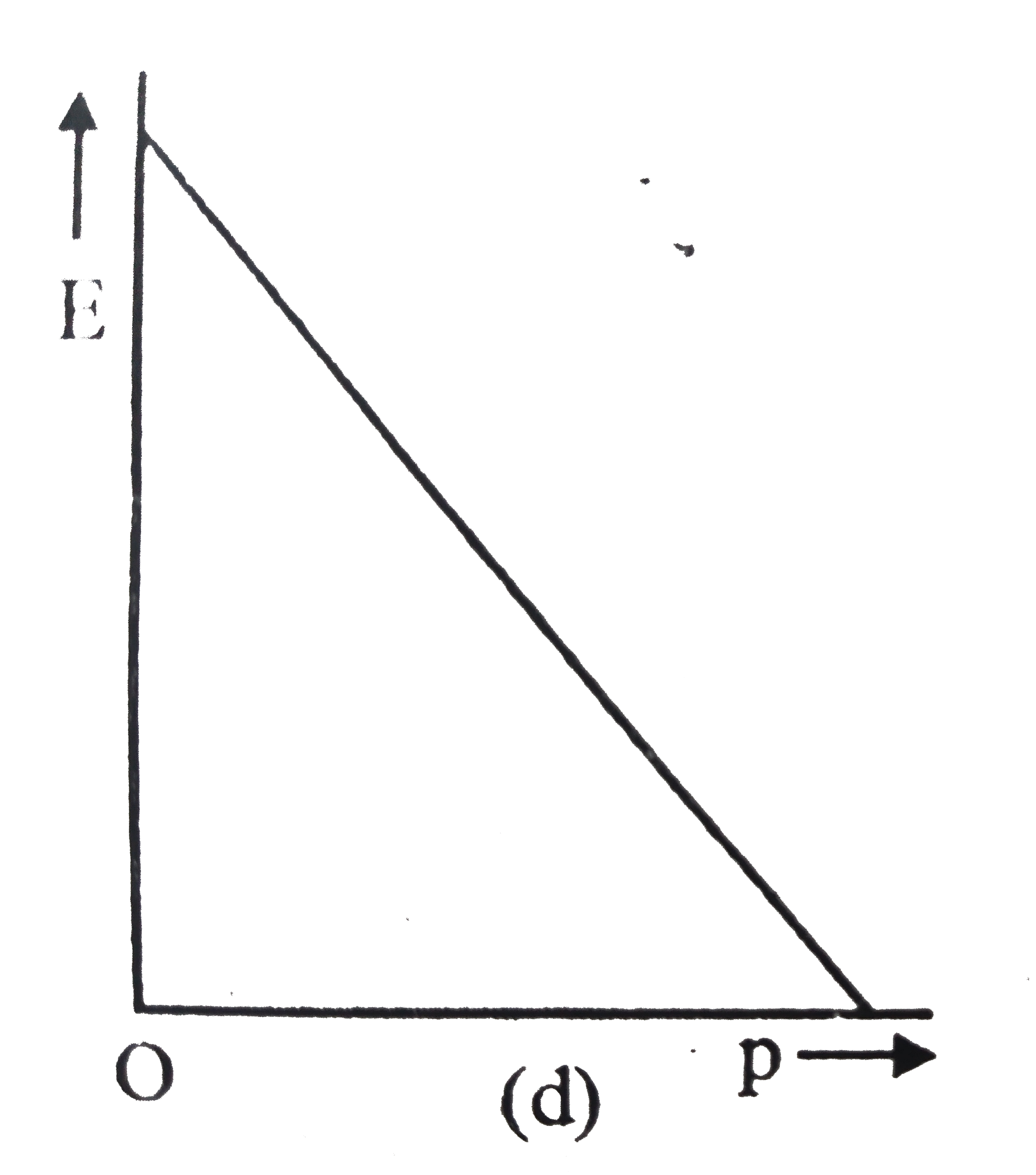
which of the following graphs correctly represents the vatiation β=−(dVdP)T/V with P for an ideal gas at constant temperature ? .
A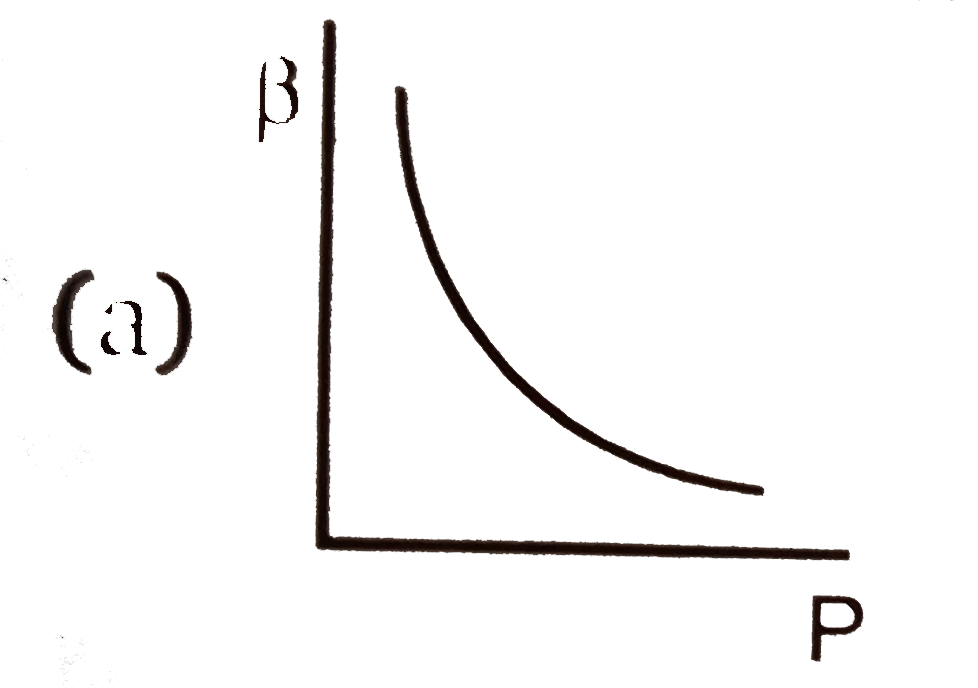 B
B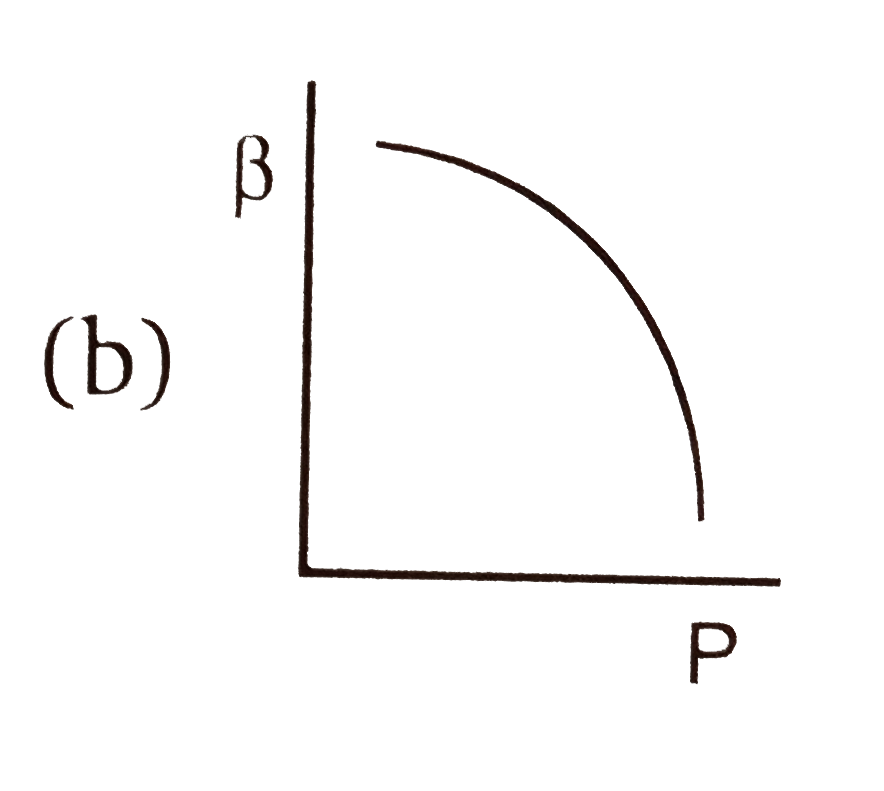 C
C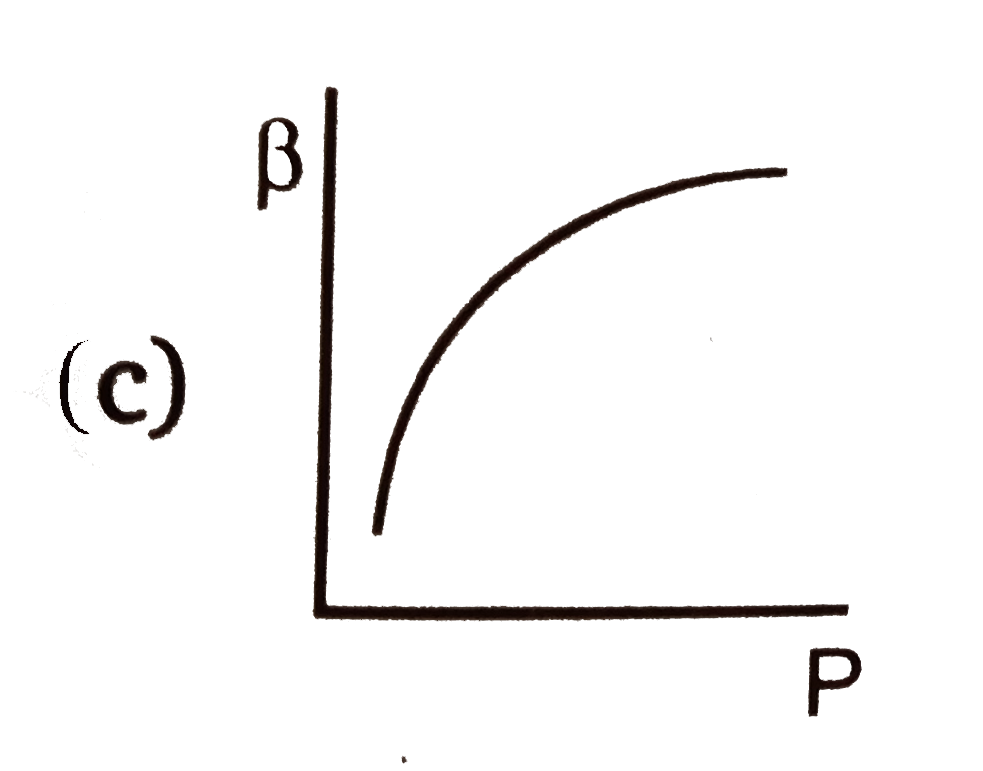 D
D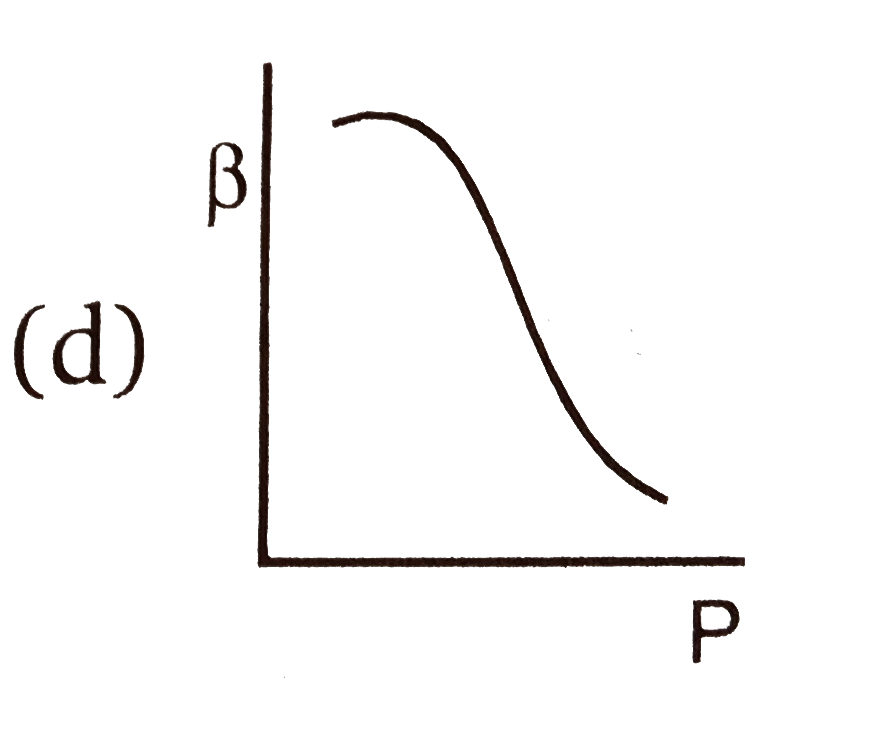
The amount of radiations emitted per second by unit area of a hollow container at 103∘ K will be-
View Solutionwhich of the following graph represents the variation of resistivity (ρ) with temperature (T) for copper?
View SolutionWhich of following graphs correctly represent variation of α=−(dV/dP)TV with P for fixed amount of an ideal gas at constant temperature ?
View SolutionWhich of the following graphs represents the variation of activity (A) of a radioactive substance with time (t).
View SolutionThe amount of thermal radiations emitted from one square metre area of a black body in one second when at a temperature of 100 K is
View Solution
