In the figure given , A and B are two particles having same magnitude of angular velocity in opposite sense, at t = 0 , then →VA−→VB at t=π2ω sec is
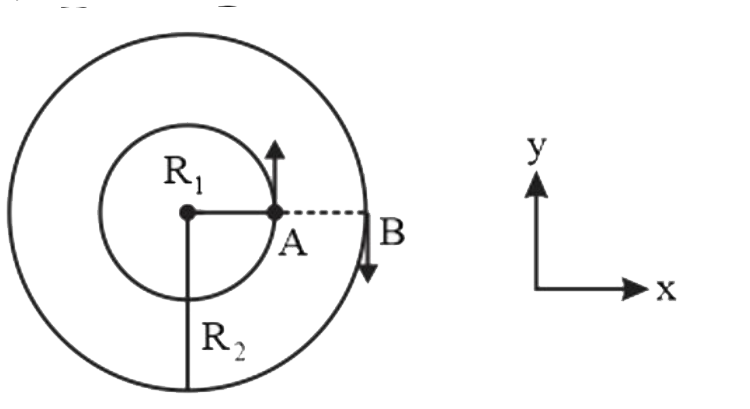
−ωR1ˆi+ωR2ˆi
ωR1ˆi−ωR2ˆj
ωR1ˆj−ωR2ˆi
ωR1ˆj+ωR2ˆj
The correct Answer is:A
Step by step video & image solution for In the figure given , A and B are two particles having same magnitude of angular velocity in opposite sense, at t = 0 , then vec(V) _(A)- vecV_B" at " t = pi/(2omega) sec is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Two Particle A and B are moving with uniform velocities of 20m/sec and 10m/sec as shown in the shown in the figure. The Magnitude of angular velocity of A with respect to B.when their separation (AB) is 10 meter is
View SolutionFind displacement of a particle in 1-D if its velocity is v=(2t−5)m/s , from t=0 to t=4 sec.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is moving on a circular path of radius R with uniform angular speed ω. The magnitude of average velocityof particle during time t=0 to t=2π3ω:
A√32ωRπB32ωRπC3√32ωRπD23ωRπ - Question 2 - Select One
Two charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field →B=B0ˆK
AThey have equal z− components of momentaBThey must have equal chargesCThey necessarily represent a partical − antipartical paritDThe charge to mass ratio satisfy :
(e/m)1+(e/m)2=0 - Question 3 - Select One
Two particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
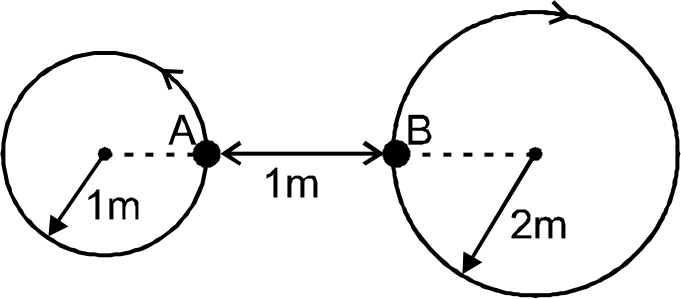
At time t=1 sec. the magnitude of acceleration of A with respect to B isAπ24√65ms2Bπ22√7ms2Cπ23√15ms2Dπ24√7ms2
A particle is performing SHM, its velocity with respect to time is V=30sin2πt, then position of particle at t=2sec is
View SolutionThe angular displacement of particle (in radian) is given by θ=t2+t. Calculate angular velocity at t=2 second.
View SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
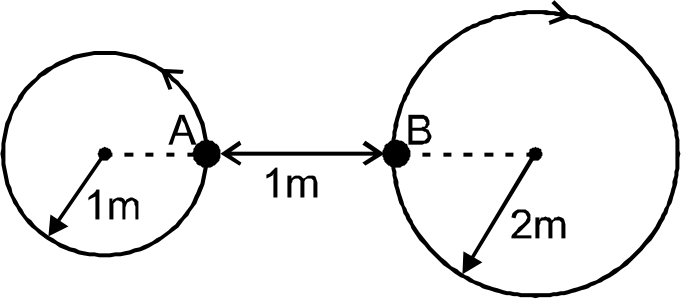
At time t=2 second, the angular velocity of the particle A with respect to the particle B isView SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
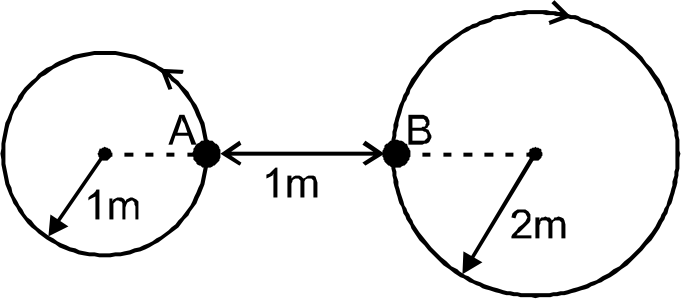
Find the magnitude of acceleration of A at t=1 secView SolutionThe acceleration of a particle is given as a=3x2 . At t = 0, v
= 0, x = 0. The velocity at t = 2 sec will be-View Solution

