In the given figure, a smooth parabolic wire track lies in the -plane (vertical). The shape of track is defined by the equation . A ring of mass which can slide freely on the wire track, is placed at the position . The track is rotated with constant angular speed such that there is no relative slipping between the ring and the track. The value of is
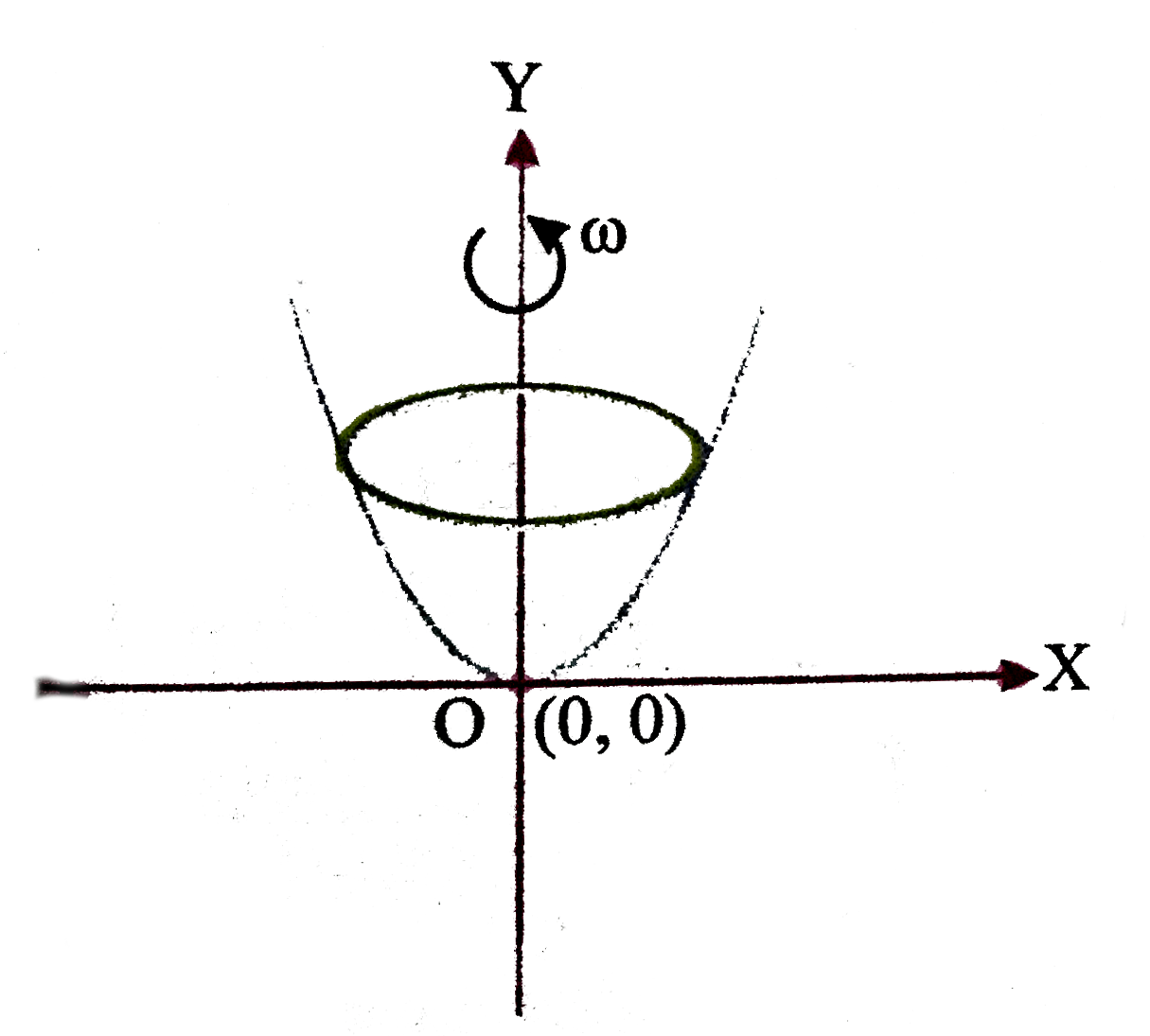
The correct Answer is:C
Step by step video & image solution for In the given figure, a smooth parabolic wire track lies in the xy-plane (vertical). The shape of track is defined by the equation y=x^(2). A ring of mass m which can slide freely on the wire track, is placed at the position A (1,1). The track is rotated with constant angular speed omega such that there is no relative slipping between the ring and the track. The value of omega is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A point charge +q is fixed at point A on the circumference of a fixed smooth non-conducting circular wire track of radius R in a gravity free space. A small ring of mass m and charge + which can slide freely on the wire track is given tangential velocity at point B which is diametrically opposite to A. If the distance of closest approach between the fixed charge and the ring is R then force applied by the wire track on the ring just after the release will be
View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length 3R/4 is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant K=mg/R. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.
View Solution
Knowledge Check
The rail gauge with a track width of 1.676m is
ABroad guageBMetre guageCNarrow guageDNone of theseA small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
AR/2BRCR/4D3R/4A small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then is equal to:
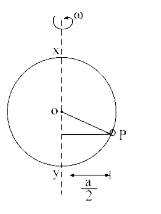A2gaBg2aC2ga√3Dg√32a
A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA smooth semicircular wire track of radius R if fixed in a vertical plane. One end of massless spring of netural length 3R4 is attached to the lowest point O of the wire track. A small ring of mass m which can slide on the track is attched to the other end of the spring. the ring is held stationary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant is K=mgR. considering the instance when the ring is released, the free body diagram of the ring, when aT is tengential acceleration, F is restoring force and N is normal reaction is
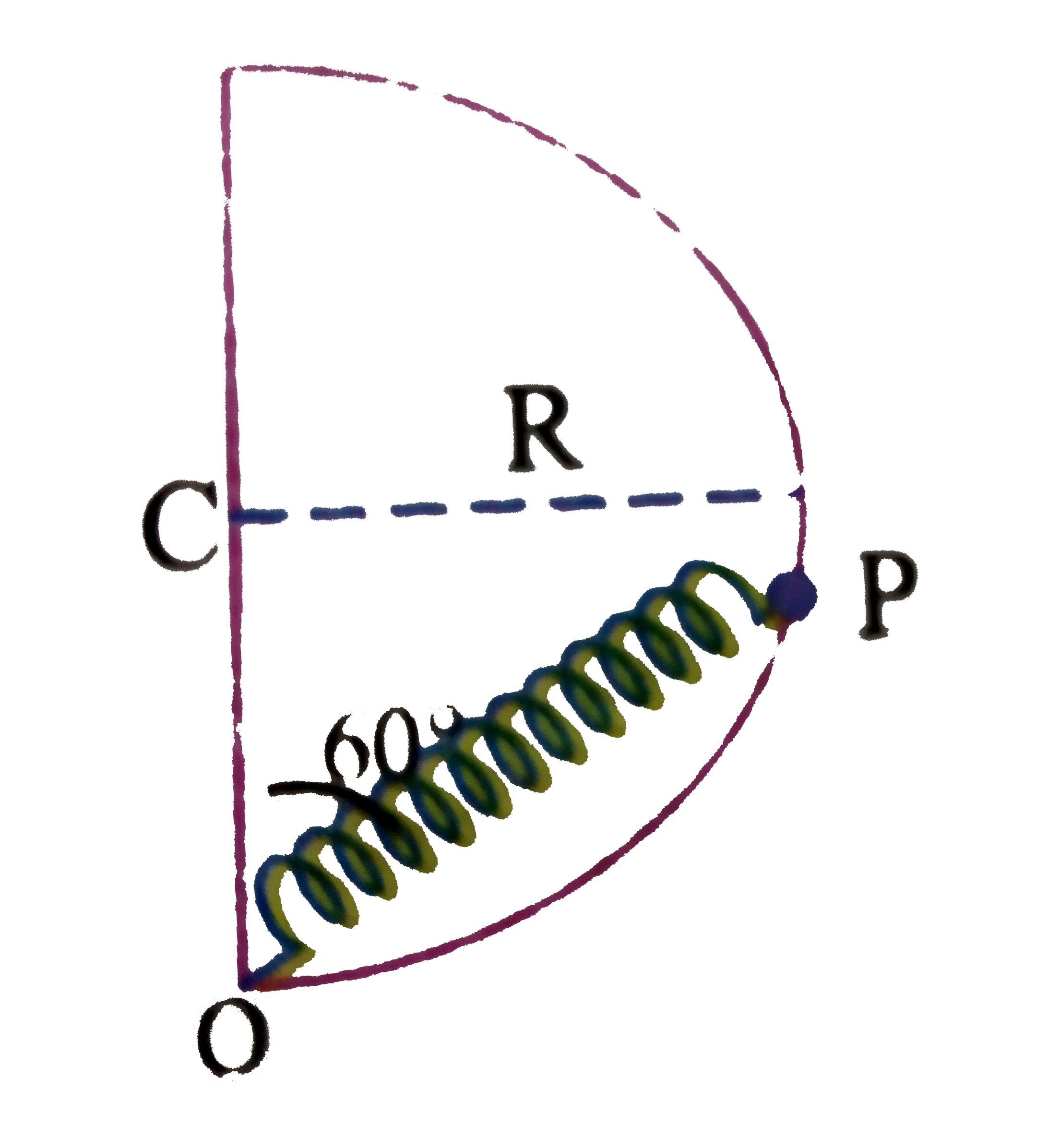
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA block of mass m is placed on a circular track and then it is given a velocity υ vertically downwards at position A on track. If block moves on track with constant speed, then
View Solution