The graph between the mass of liquid inside the capillary and radius of capillary is
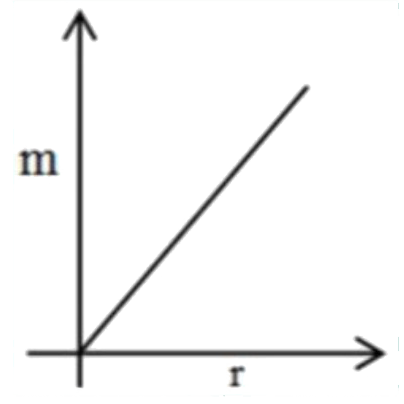
The correct Answer is:C
To solve the problem of finding the relationship between the mass of liquid inside a capillary tube and the radius of the capillary, we can follow these steps:
Step 1: Understand the Capillary Rise Formula
The height of capillary rise (H) is given by the formula:
H=2ScosθRρg
where:
- S = surface tension of the liquid,
- θ = angle of contact,
- R = radius of the capillary tube,
- ρ = density of the liquid,
- g = acceleration due to gravity.
Step 2: Relate Height to Volume
The volume (V) of liquid that rises in the capillary can be expressed as:
V=πR2H
where πR2 is the cross-sectional area of the capillary tube.
Step 3: Substitute Height in Volume Equation
Substituting the expression for H into the volume equation gives:
V=πR2(2ScosθRρg)
This simplifies to:
V=2SπRcosθρg
Step 4: Relate Volume to Mass
The mass (m) of the liquid can be expressed as:
m=ρV
Substituting the expression for V gives:
m=ρ(2SπRcosθρg)
This simplifies to:
m=2SπcosθgR
Step 5: Identify the Relationship
From the equation m=2SπcosθgR, we can see that mass (m) is directly proportional to the radius (R):
m∝R
Step 6: Graphical Representation
Since mass is directly proportional to radius, the graph of mass (m) versus radius (R) will be a straight line passing through the origin. This means that as the radius increases, the mass of the liquid inside the capillary also increases linearly.
Final Conclusion
The graph between the mass of liquid inside the capillary and the radius of the capillary is a straight line passing through the origin.
---
The height of capillary rise (H) is given by the formula:
H=2ScosθRρg
where:
- S = surface tension of the liquid,
- θ = angle of contact,
- R = radius of the capillary tube,
- ρ = density of the liquid,
- g = acceleration due to gravity.
The volume (V) of liquid that rises in the capillary can be expressed as:
V=πR2H
where πR2 is the cross-sectional area of the capillary tube.
Substituting the expression for H into the volume equation gives:
V=πR2(2ScosθRρg)
This simplifies to:
V=2SπRcosθρg
The mass (m) of the liquid can be expressed as:
m=ρV
Substituting the expression for V gives:
m=ρ(2SπRcosθρg)
This simplifies to:
m=2SπcosθgR
From the equation m=2SπcosθgR, we can see that mass (m) is directly proportional to the radius (R):
m∝R
Since mass is directly proportional to radius, the graph of mass (m) versus radius (R) will be a straight line passing through the origin. This means that as the radius increases, the mass of the liquid inside the capillary also increases linearly.
The graph between the mass of liquid inside the capillary and the radius of the capillary is a straight line passing through the origin.
Topper's Solved these Questions
Similar Questions
A capillary tube of radius r is immersed vertically in a liquid such that liquid rises in it to height h (less than the length of the tube). Mass of liquid in the capillary tube is m. If radius of the capillary tube is increased by 50%, then mass of liquid that will rise in the tube, is
View SolutionThe rise of a liquid inn a capillary tube depends on
View Solution
Knowledge Check
The liquid rise in capillary-
Ais directly proportional to the thickness of glassBis inversely proportional to the thickness of glassCis proportional to the square of the thickness of glassDdoes not depend on the thickness of the glassThe graph between the height of liquid in a capillary tube against the radius of the tube for a liquid , then the graph is
Aa straight line passing through origin with a positive slopeBa straight line passing through origin with a negative slopeCa rectangular hyperbolaDa parabolaIf liquid level falls in a capillary then radius of capillary will
AIncreasesBDecreasesCUnchangedDNone of these
The most approprite graph between height (h) of the liquid column in a capillary tube and the radius ( r ) of the tube for a given liquid will be
View SolutionA capillary tube of radius r is immersed vertically in a liquid such that liquid rises in it to height h (less than the length of the tube). Mass of liquid in the capillary tube is m. If radius of the capillary tube is increased by 50%, then mass of liquid that will rise in the tube, is
View SolutionThe rise of liquid in a capillary tube depends on :
View SolutionThe rise of a liquid in a capillary tube is due to :
View SolutionThe rise of a liquid in a capillary tube is due to :
View Solution
