A wire is bent to form a semicircle of the radius a. The wire rotates about its one end with angular velocity ω . Axis of rotation is perpendicular to the plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the aixs of rotation as shown in the figure . Then -
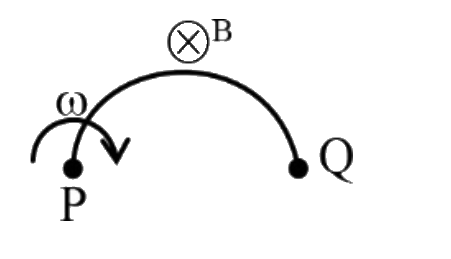
Potential difference between P and Q is equal to 2Bωa2
Potential difference between P and Q is equal to 2π2Bωa2
P is at higher potential than Q
none of these
The correct Answer is:A
Step by step video & image solution for A wire is bent to form a semicircle of the radius a. The wire rotates about its one end with angular velocity omega . Axis of rotation is perpendicular to the plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the aixs of rotation as shown in the figure . Then - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
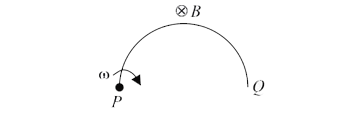
A wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
View SolutionA circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
View Solution
Knowledge Check
a semicircle wire of radius R is rotated with constant angular velocity about an axis passing through one end and perpendicular to the plane of wire. There is a uniform magnetic field of strength B. The induced emf between the ends is
 A(a) BωR2/2B(b) 2BωR2C( c) is variableD(d) none of these
A(a) BωR2/2B(b) 2BωR2C( c) is variableD(d) none of theseIn a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of the circle with an angular frequency ω. The axis of rotation is perpendicular to the field. If the total resistance of the circuit is R, the mean power generated per period of rotation is
A(Bπrω)22RB(Bπr2ω)28RCBπr2ω2RD(Bπrω2)28R
A wire is in the form of a semicircle of radius r. One end is attached to an axis about which it rotates with an angular speed ω. The axis is normal to the plane of the semicircle. The wire is immersed in a uniform magnetic field B parallel to the axis. find the induced emf between points o and P of the semicircle.

View SolutionA ring rotates with angular velocity ω about an axis perpendicular to the plane of the ring passing through the center of the ring.A constant magnetic field B exists parallel to the axis.Find the emf induced in the ring.

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionA ring rotates with angular velocity ω about an axis perpendicula to the plane of the ring passing through the center of the ring (Fig. 3.77). A constant magnetic field B exists parallel to the axis. Find the emf induced in the ring.

View SolutionA semicircular wire of radius R= 20 cm rotates in its own plance about one end with angular velocity w=10rad/s in unifornm magnetic field B=5 mT perpendicular into the plane of the wire gtFind the voltage developend between the ends of the wire
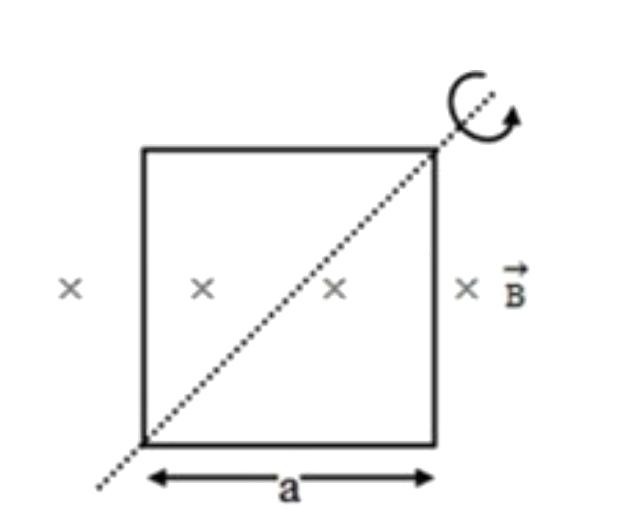
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View Solution
