The displacement of two identical particles executing SHM are represented by equations x1=4sin(10t+π6)&x2=5cos(ωt) For what value of ω, energy of both the particles is same.
16 unit
6 unit
4 unit
8 unit
The correct Answer is:D
Step by step video, text & image solution for The displacement of two identical particles executing SHM are represented by equations x_(1) = 4 sin (10t+(pi)/(6)) & x_(2) = 5 cos (omegat) For what value of omega, energy of both the particles is same. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The displacement of two identical particles executing SHM are represented by equations.
x1=4sin(10t+π6) and x2=5cosεt
For what value of epsilon of both the particles is same?A16 unitB6 unitC4 unitD8 unitThe displacement of two particles executing SHM are represented by equations, y1=2sin(10t+θ),y2=3cos10t. The phase difference between the velocity of these particles is
AθB−θCθ+π/2Dθ−π/2The equation of the displacement of two particles making SHM are represented by y1=asin(ωt+ϕ)&y2−acos(ωt). Phase difference between velocities of two particles is
Aπ2+ϕB−ϕCϕDϕ−π2
What is the phase difference between two simple harmonic motions represented by x1=Asin(ωt+π6) and x2=Acos(ωt)?
View SolutionThe displacement of a particle executing SHM is given by
Y=5 sin (4t+π3)
If T is the time period and the mass of the particle is 2g, the kinetic energy of the particle When t=T4 is given by-
View SolutionThe displacement (x) is plotted with time (t) for a particle executing SHM as shown below. The correct equation of SHM is
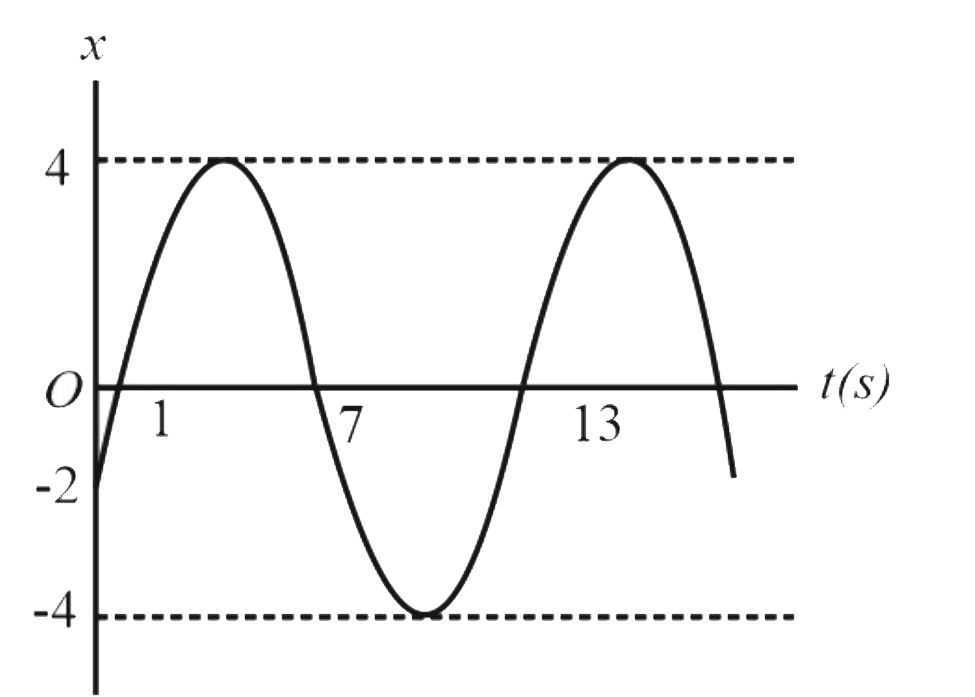
View SolutionThe displacement of a particle executing SHM at any time t (Seconds) is x=0.01sin100π(t=0.005) then its time period will be
View SolutionThe displacement of a particle is represented by the equation y=3cos(π4−2ωt).
The motion of the particle is
View Solution
