A wooden object floats in water kept in as beaker. The object is near a side of the beaker figure. Let P1,P2,P3 be the pressure at the three points A,B and C of the bottom as shown in the figure.

P1=P2=P3
P1<P2<P3
P1>P2>P3
P1=P2≠P3
The correct Answer is:A
Step by step video & image solution for A wooden object floats in water kept in as beaker. The object is near a side of the beaker figure. Let P_1,P_2,P_3 be the pressure at the three points A,B and C of the bottom as shown in the figure. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
An object of uniform density is allowed to float in water kept in a beaker. The object has triangular cross-section as shown in the figure. If the water pressure measured at the three points A, B and C below the object are PA,PB and PC respectively. Then
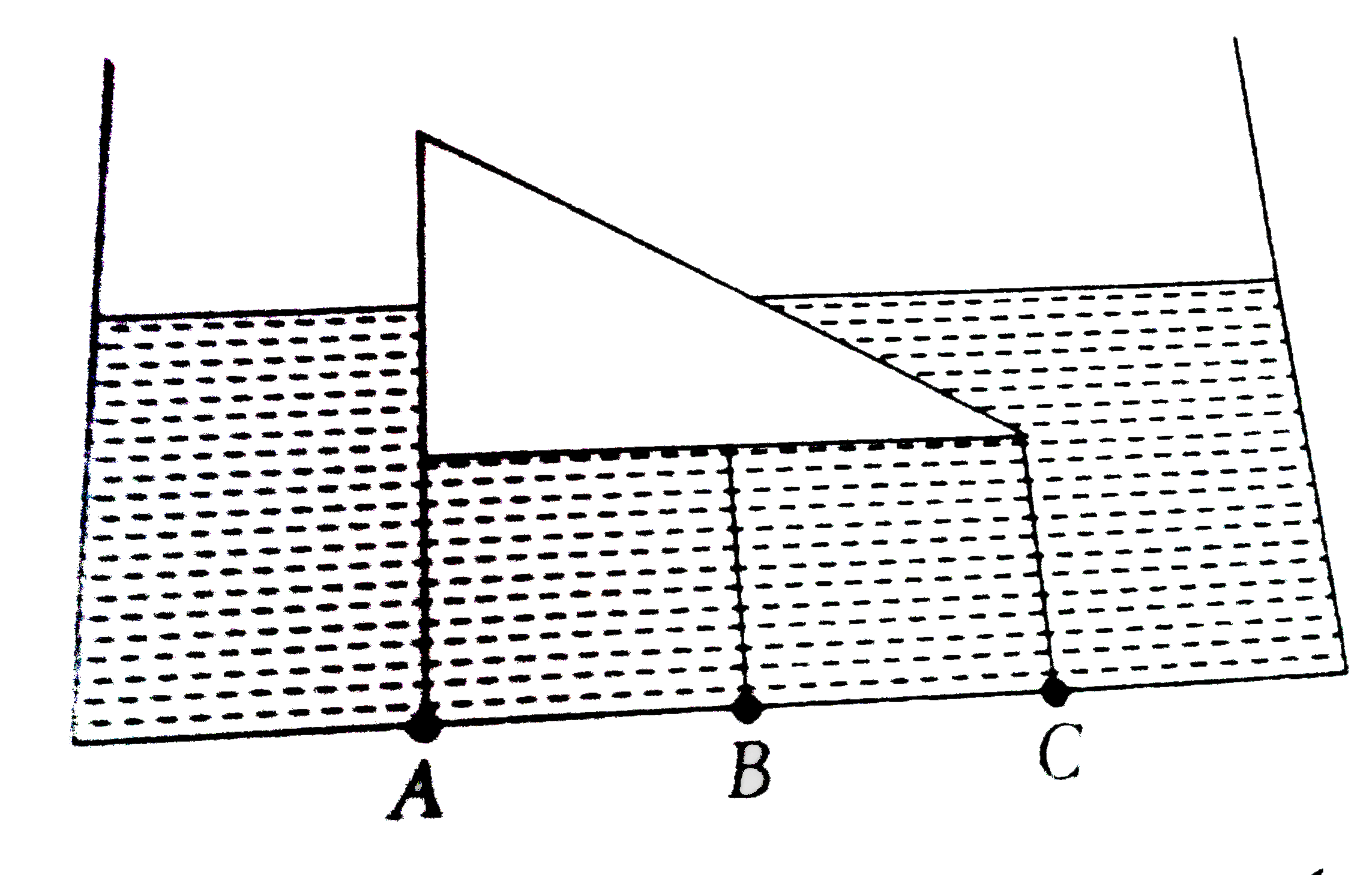 ApA>pB>pCBpA>pB<pCCpA=pB=pCDpA=pB<pC
ApA>pB>pCBpA>pB<pCCpA=pB=pCDpA=pB<pCA wooden block is floating on water kept in a beaker. 40% of the block is above the water surface. Now the beaker is kept inside a lift that starts going upward with acceleration equal to g/2. The block will then
AsinkBfloat with 10% above the water surfaceCfloat with 40% above the water surfaceDfloat with 70% above the water surfaceFor V versus T curves at constant pressure P1andP2 for and ideal gas shown in figure-
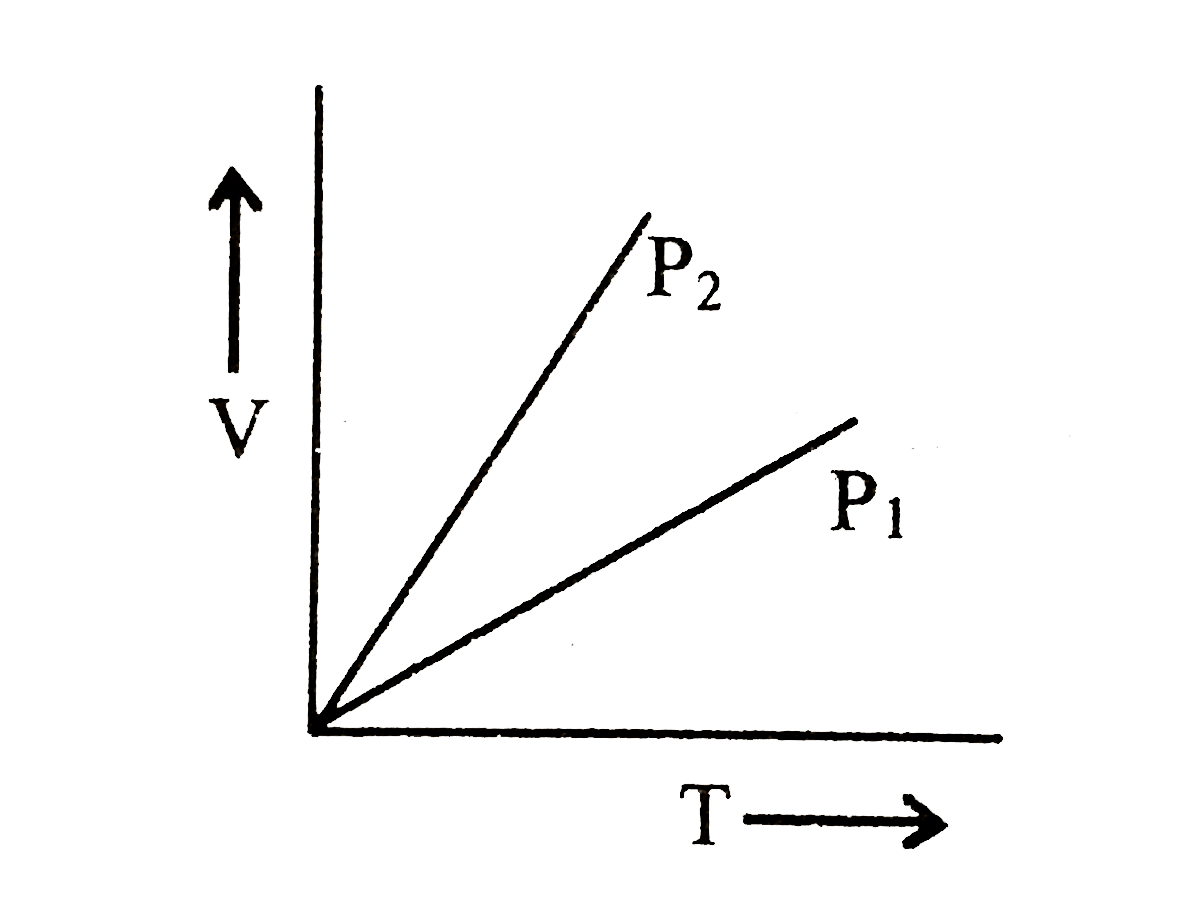 AP1>P2BP1<P2CP1=P2DP1P2
AP1>P2BP1<P2CP1=P2DP1P2
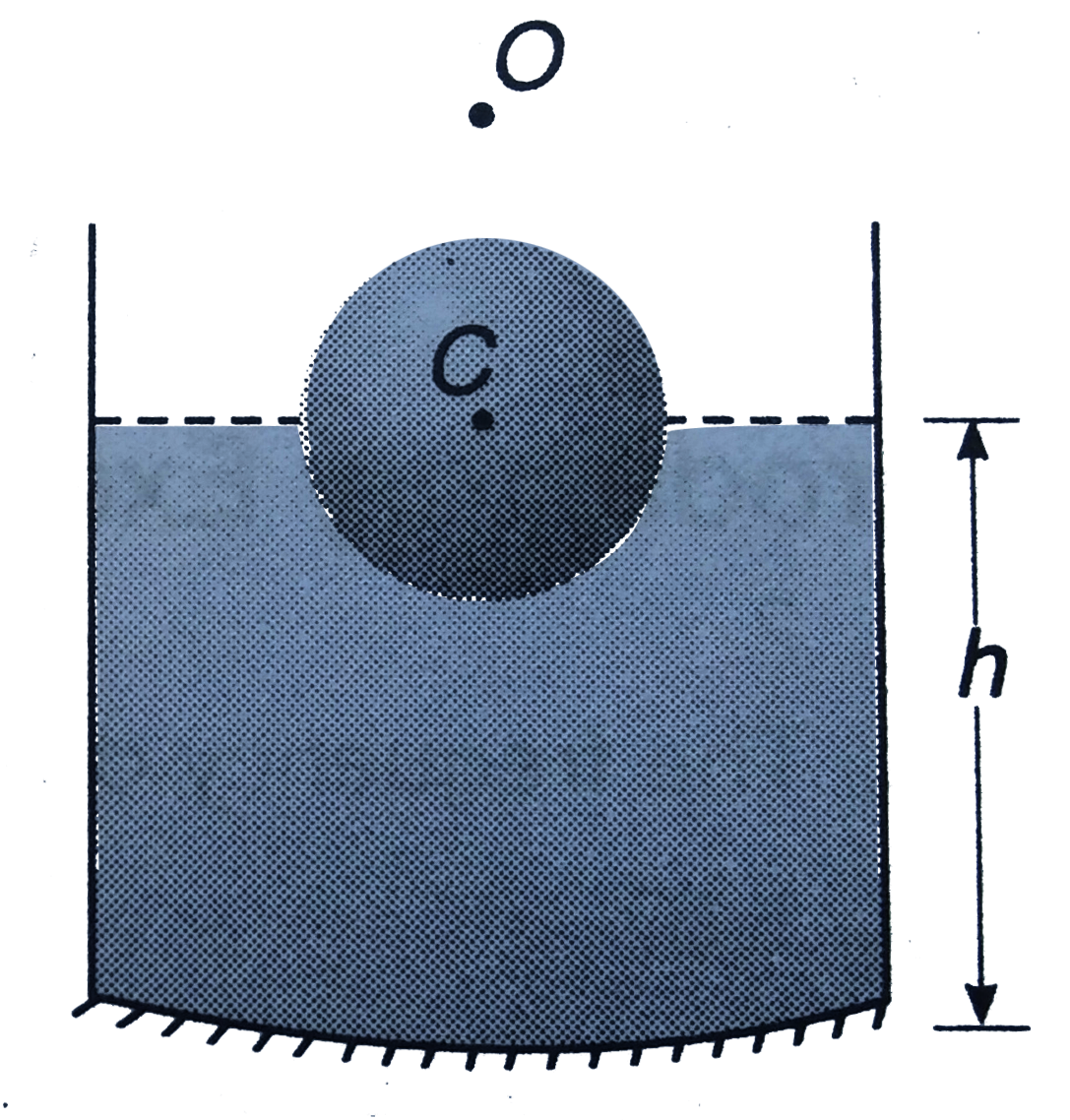
A transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
View SolutionA liquid of density ρ is filled in a beaker of cross section A to a height H and then a cylinder of mass M and cross-section a is made to float in it as shown in

If the atmospheric pressure is P0 find the pressure (a) at the top face B of the cylinder (b) at the bottom face C of the cylinder and (c ) at the base D of the beaker. (d) Can ever these pressure be equal ?
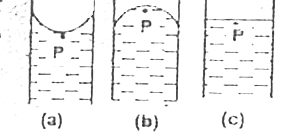
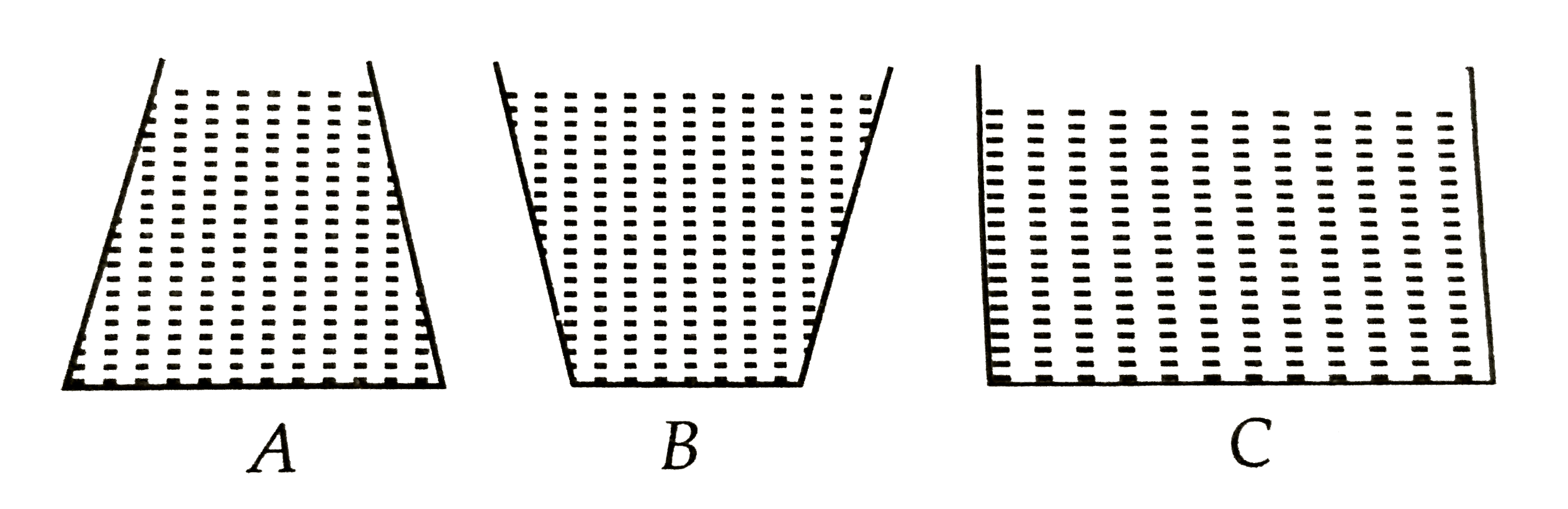
View SolutionThree vessels A,B,and C of different shapes contain a water upto the same height as shown in the figure .PA,PB ,and PC be the pressure exerted by the water at the bottom of the vessels A ,B and C respectively . Then
View SolutionA light ray from an object 'P' is reflected from a mirror as shown in the figure, then
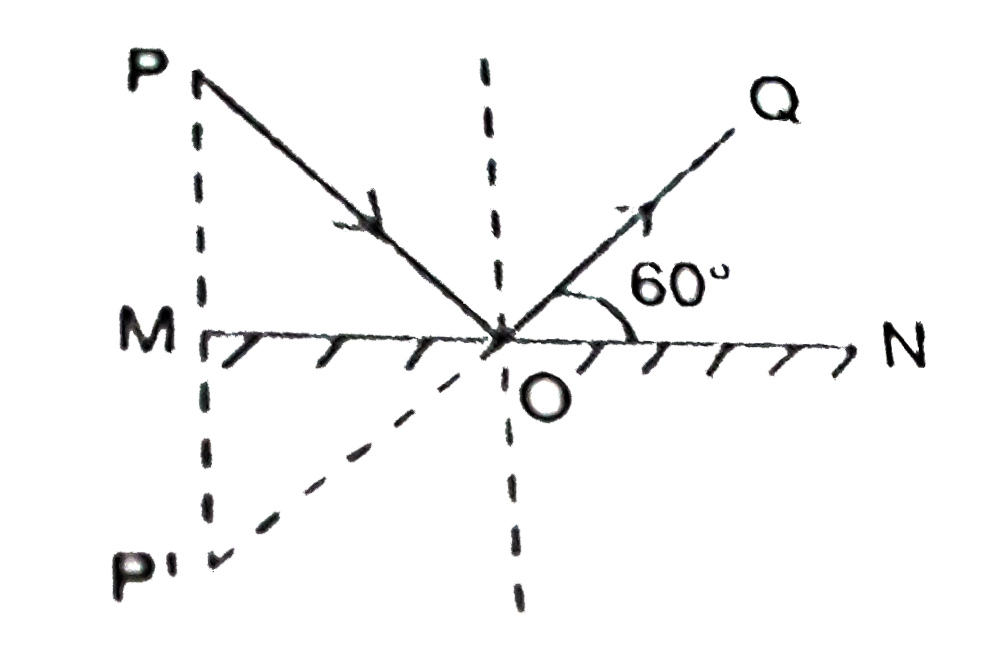
View SolutionA light ray from an object 'P' is reflected from a mirror as shown in the figure, then

View Solution