A conductor of length L is placed along the x - axis , with one of its ends at x = 0 and the other at x = L. If the rate of flow of heat energy through the conduct is constant and its thermal resistance per unit length is also constant , then Which of the following graphs is/are correct ?
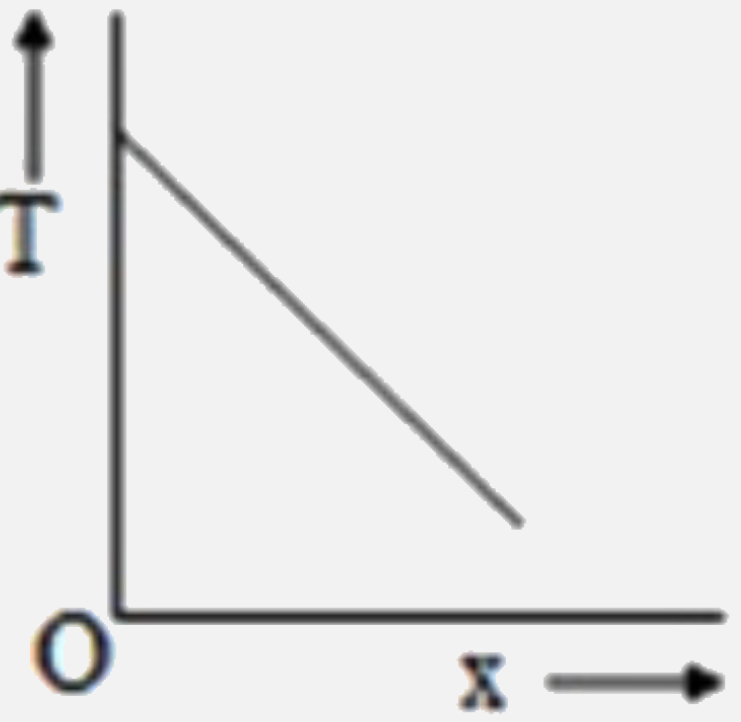
The correct Answer is:C
To solve the problem, we need to analyze the heat flow through a conductor and how temperature varies along its length.
1. Understanding the Problem:
We have a conductor of length L placed along the x-axis, with one end at x=0 and the other at x=L. The rate of heat flow through the conductor is constant, and the thermal resistance per unit length is also constant.
2. Using the Heat Flow Equation:
The rate of heat flow dqdt through the conductor can be expressed using Fourier's law of heat conduction:
dqdt=−kA(T−T0)L
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- T is the temperature at position x,
- T0 is the temperature at the other end of the conductor.
3. Rearranging the Equation:
We can rearrange the equation to express temperature T as a function of position x:
T(x)=−dqdtxkA+T0
This equation shows that T(x) is a linear function of x.
4. Identifying the Graph Characteristics:
- The slope of the temperature vs. position graph is negative, indicating that as we move along the conductor from x=0 to x=L, the temperature decreases.
- The y-intercept of the graph is T0, which is positive.
5. Analyzing the Given Graph Options:
- Option 1: Slope is positive (incorrect).
- Option 2: No intercept (incorrect).
- Option 3: Negative slope with a positive intercept (correct).
- Option 4: Not a straight line (incorrect).
6. Conclusion:
The correct graph that represents the relationship between temperature and position along the conductor is Option 3.
We have a conductor of length L placed along the x-axis, with one end at x=0 and the other at x=L. The rate of heat flow through the conductor is constant, and the thermal resistance per unit length is also constant.
The rate of heat flow dqdt through the conductor can be expressed using Fourier's law of heat conduction:
dqdt=−kA(T−T0)L
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- T is the temperature at position x,
- T0 is the temperature at the other end of the conductor.
We can rearrange the equation to express temperature T as a function of position x:
T(x)=−dqdtxkA+T0
This equation shows that T(x) is a linear function of x.
- The slope of the temperature vs. position graph is negative, indicating that as we move along the conductor from x=0 to x=L, the temperature decreases.
- The y-intercept of the graph is T0, which is positive.
- Option 1: Slope is positive (incorrect).
- Option 2: No intercept (incorrect).
- Option 3: Negative slope with a positive intercept (correct).
- Option 4: Not a straight line (incorrect).
The correct graph that represents the relationship between temperature and position along the conductor is Option 3.
Topper's Solved these Questions
Similar Questions
A straight rod of length L has one of its end at the origin and the other at X=L. If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is λ such that λ=a+bx. Find the mass of the rod.
View Solution
Knowledge Check
When a steel wire fixed at one end is pulled by a constant force F at its other end , its length increases by l.Which of the following statements is not correct?
Awork done by the external force is FL.Bsome heat is produced in the wire in the processCthe elastic potential energy of the wire is FL2Dthe heat produced is equal to the half of the elastic potential energy stored in the wireA thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as k(xL)n where n can be zero or any positive number. If the position XCM of the centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of XCM on n?
A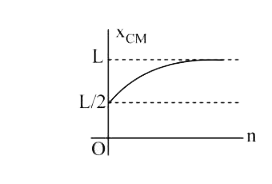 B
B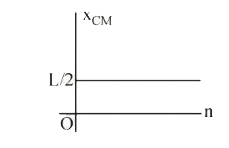 C
C D
D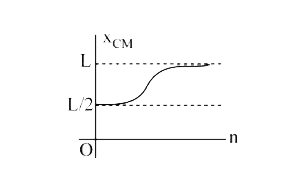
A thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as k(xL)n where n can be zero or any positive integer. If position Xcm of centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of xCM on n?
A B
B C
C D
D
A rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/ length) λ of the rod varies with the distance x from the origin as λ=Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/length) λ of the rod varies with the distance x from the origin as λ = Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
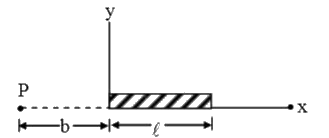
View SolutionA rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -
View SolutionA uniform rod of length l is being rotated in a horizontal plane with a constant angular speed about an axis passing through one of its ends. If the tension generated in the rod due to rotation is T(x) at a distance x from the axis, then which of the following graphs depicts it most closely ?
View SolutionA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
View Solution
