A parabolic bow1 with its bottom at origin has the shape y=x220 where x and y are in metre The maximum height at which a small mass m can be placed on the bowl without slipping is (coeff of static friction 0.5
 .
.
2.5 m
1.25 m
1.0 m
4.0 m
The correct Answer is:B
Step by step video & image solution for A parabolic bow1 with its bottom at origin has the shape y = (x^(2))/(20) where x and y are in metre The maximum height at which a small mass m can be placed on the bowl without slipping is (coeff of static friction 0.5 . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle moves with a uniform speed of 2m/s in x-y plane according to the equation y=4x2 , where x and y are in metre. The acceleration of the particle along y -axis while passing through the origin has magnitude?
View SolutionA block of mass 'm' is placed on a rough surface with a vertical cross section of y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is .
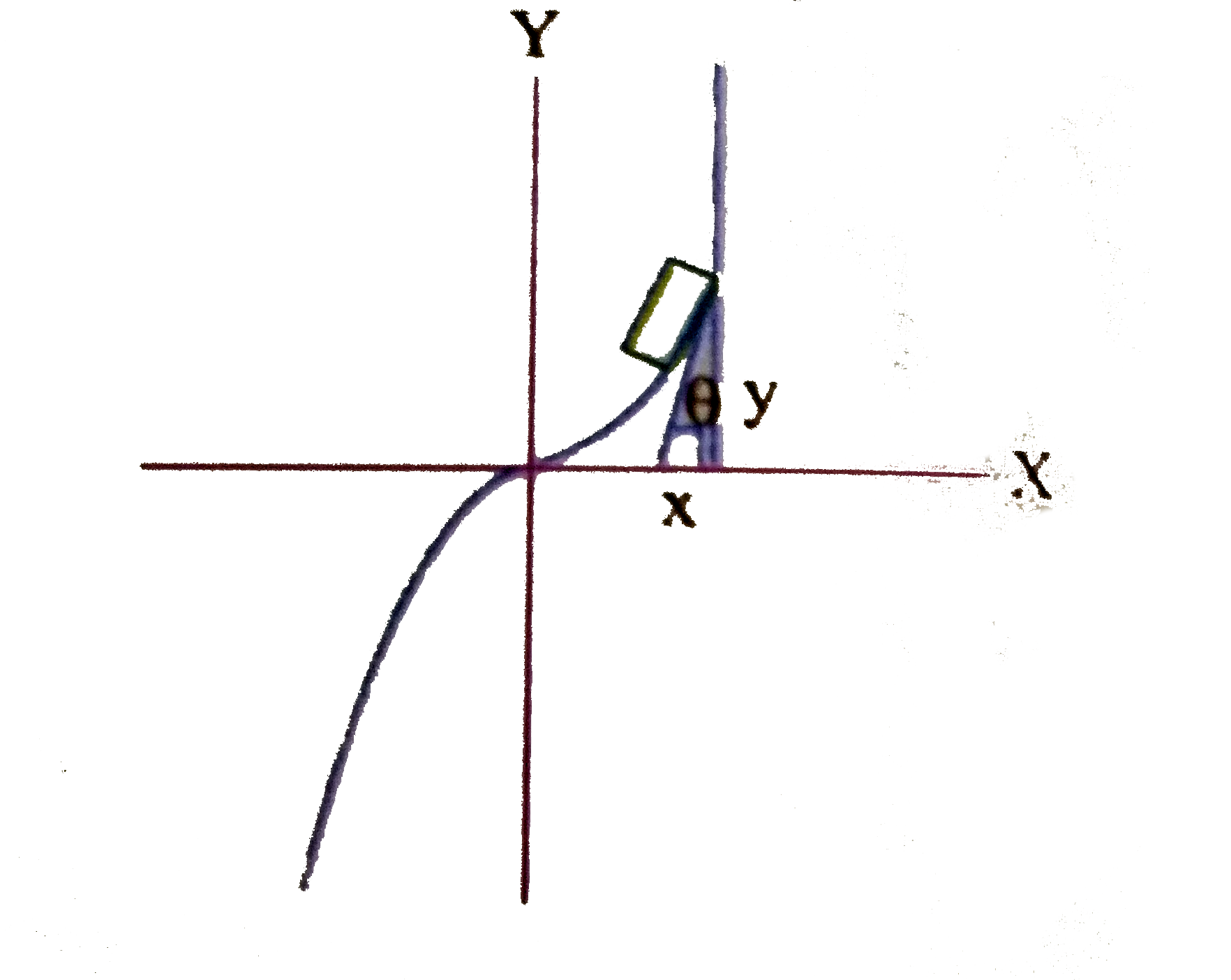
View Solution
Knowledge Check
A particle of mass 1 kg is moving along the line y = x + 2 (here x and y are in metres) with speed 2 m/s. The magnitude of angular momentum of particle about its origin is
A4kgm2s−1B2√2kgm2s−1C4√2kgm2s−1D2kgm2s−1A particle of mass 1 kg is moving along the line y=x+2 (here x and y are in metres) with speed 2m/s. The magnitude of angular momentum of paticle about origin is -
A4kg−m2/sB2√2kg−m2/sC4√2kg−m2/sD2kg−m2/sIf x2+x+y2−1=0, where x > 0 and y > 0 then maximum value of x√y is
A13√2B12√2C√2D2√2
If x2+x=1−y2 , where x>0,y>0, then find the maximum value of x√y.
View SolutionThe equation of a progressive wave is given by y=0.5sin(20x−400t) where xand y are in metre and tis in second. The velocity of the wave is
View SolutionThe equation of a travelling wave is given by
y = 0.5 sin(20x - 400t)
where x and y are in metre and t is in second. The velocity of the wave is :
View SolutionThe equation of a travelling wave is given by
y = 0.5 sin(20x - 400t)
where x and y are in metre and t is in second. The velocity of the wave is :
View SolutionA block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
View Solution
