In a potentiometer experiment if the voltage across resistance R and R + r are balanced at the length l1andl2 respectively the value of resistance r will be
(l1−l2l2)R
(l1−l2l1)R
(l2−l1l1)R
(l2−l1l2)R
The correct Answer is:C
To solve the problem, we need to analyze the potentiometer experiment and derive the expression for the resistance r based on the given lengths l1 and l2.
1. Understanding the Potentiometer Setup:
- In a potentiometer, the voltage drop across a wire of length l is proportional to the length of the wire. The resistance per unit length is denoted as λ (in ohms/meter).
- When a jockey is placed at length l1, it balances the resistance R.
- When the jockey is placed at length l2, it balances the resistance R+r.
2. Setting Up the Equations:
- For the first case (length l1):
V=I⋅R(Ohm's Law)
The voltage drop across the potentiometer wire of length l1 is:
V=λ⋅l1
Therefore, we can write:
R=λ⋅l1(1)
- For the second case (length l2):
The voltage drop across the potentiometer wire of length l2 is:
V=λ⋅l2
Thus, we have:
R+r=λ⋅l2(2)
3. Subtracting the Equations:
- Now, we will subtract equation (1) from equation (2):
(R+r)−R=λ⋅l2−λ⋅l1
Simplifying this gives:
r=λ⋅(l2−l1)(3)
4. Expressing λ:
- From equation (1), we can express λ:
λ=Rl1
- Substituting this value of λ into equation (3):
r=Rl1⋅(l2−l1)
5. Final Expression:
- Therefore, the value of the resistance r is:
r=R⋅(l2−l1)l1
Conclusion:
The value of resistance r is given by:
r=R⋅(l2−l1)l1
- In a potentiometer, the voltage drop across a wire of length l is proportional to the length of the wire. The resistance per unit length is denoted as λ (in ohms/meter).
- When a jockey is placed at length l1, it balances the resistance R.
- When the jockey is placed at length l2, it balances the resistance R+r.
- For the first case (length l1):
V=I⋅R(Ohm's Law)
The voltage drop across the potentiometer wire of length l1 is:
V=λ⋅l1
Therefore, we can write:
R=λ⋅l1(1)
The voltage drop across the potentiometer wire of length l2 is:
V=λ⋅l2
Thus, we have:
R+r=λ⋅l2(2)
- Now, we will subtract equation (1) from equation (2):
(R+r)−R=λ⋅l2−λ⋅l1
Simplifying this gives:
r=λ⋅(l2−l1)(3)
- From equation (1), we can express λ:
λ=Rl1
- Substituting this value of λ into equation (3):
r=Rl1⋅(l2−l1)
- Therefore, the value of the resistance r is:
r=R⋅(l2−l1)l1
The value of resistance r is given by:
r=R⋅(l2−l1)l1
Topper's Solved these Questions
Similar Questions
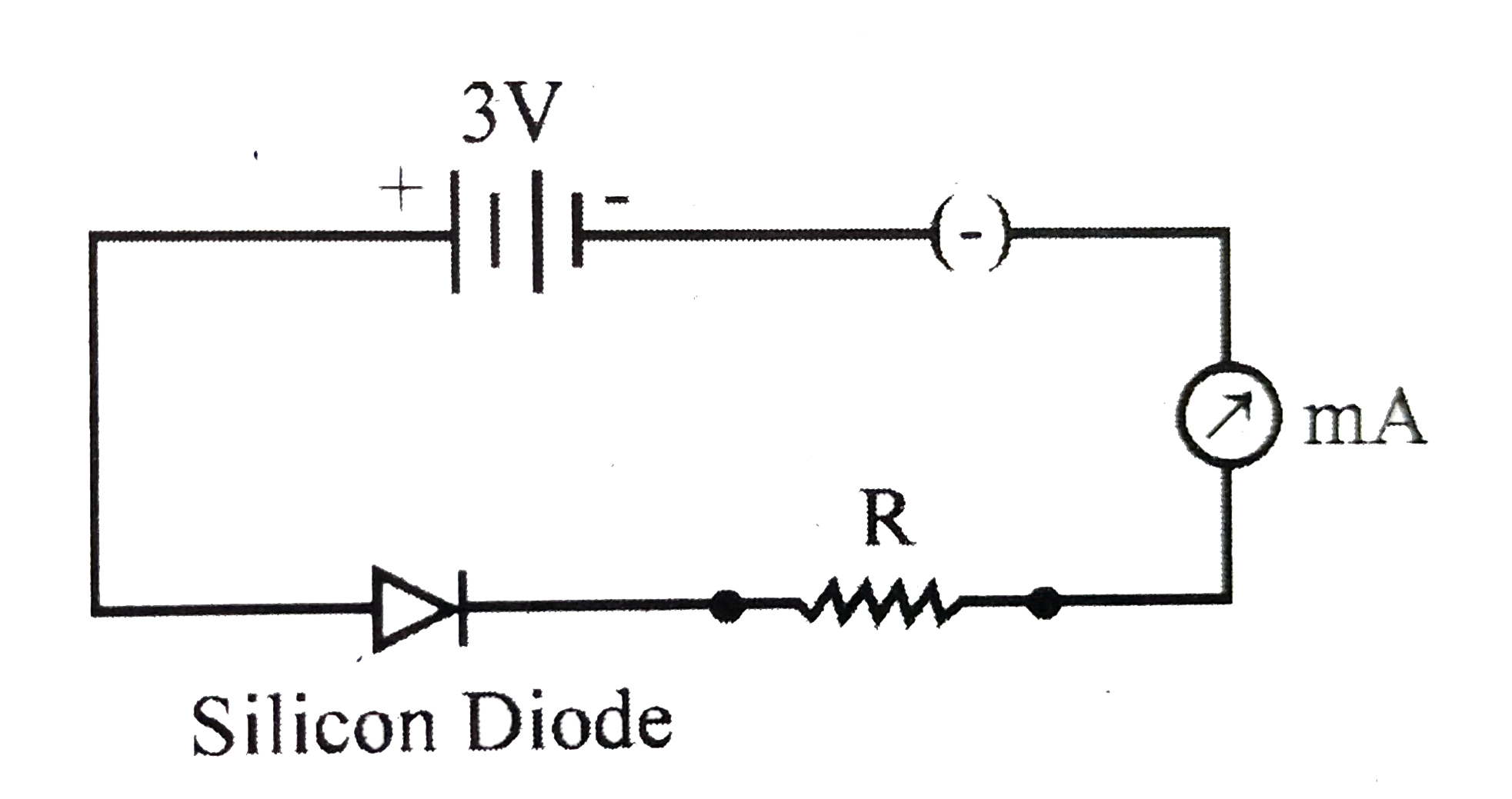
In the above circuit, the voltage drop across the resistance (R) is
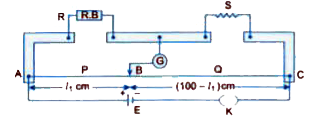
View SolutionWhat is end error in a metre bridge ? How is it overcome ? The resistances in the two arms of the metre bridge are R=5Ω and S respectively. When the resistance S is shunted with an equal resistance, the new balance length found to be 1.5l1, where l1 is the initial balancing length. Calculate the value of S.
View Solution
Knowledge Check
In an L-C-R circuit the AC voltage across R, L and C comes out as 10 V , 10 V and 20 V respectively . The voltage across the enter combination will be
A30 VB10√3VC20 VD10√2AIn potentiometer experiment, if l1 is the balancing length for e.m.f. of the cell of internal resistance r and l2 is the balancing length for its terminal potential difference when shunted with resistance R then :
Al1=l2(R+RR)Bl1=l2(RR−r)Cl1=l2(RR+r)Dl1=l2(R−rR)
A uniform potentiometer wire AB of length 100 cm has a resistance of 5Ω and it is connected in series with an external resistance R and a cell of emf 6 V and negligible internal resistance. If a source of potential drop 2 V is balanced against a length of 60 cm of the potentiometer wire, the value of resistance R isA1ΩB2ΩC4ΩD6Ω
In a series L-C-R circuit the voltage across resistance , capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
View Solution
If L= inductance and R = resistance, then the unit of L/R is:
View SolutionIn potentiometer experiment, if l1 is the balancing length for e.m.f. of the cell of internal resistance r and l2 is the balancing length for its terminal potential difference when shunted with resistance R then :
View SolutionA cell of emf (E) and internal resistance (r) is balanced across (l) length of potentiometer wire. If another cell of emf 2E and internal resistance (2r) is connected in parallel to the first cell , then the balancing length will be
View SolutionIn the determination of the internal resistance of a cell using a potentiometer, when the cell is shunted by a resistance R and connected in the secondary circuit, the balance length is found to be L1. On doubling the shunt resistance, the balance length is found to increase to L2. The value of the internal resistance is
View Solution
