A particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
its displacement will be in simple harmonic
its velocity will be in simple harmonic
its acceleration will be in simple harmonic
None of the above
The correct Answer is:D
To solve the problem, we need to analyze the given force acting on the particle and determine whether the motion of the particle can be classified as simple harmonic motion (SHM).
1. Identify the Force: The force acting on the particle is given by:
F=t2−kx
where k is a constant, x is the displacement, and t is time.
2. Understand the Conditions for SHM: For a motion to be classified as simple harmonic motion, the restoring force must be directly proportional to the negative of the displacement:
F=−kx
This means that the force should only depend on the displacement x and not on time t.
3. Compare the Given Force with SHM Condition: In the given force equation, we have an additional term t2 which depends on time. This means that the force is not solely dependent on the displacement x.
4. Conclusion about SHM: Since the force F=t2−kx includes a time-dependent term, it cannot satisfy the condition for simple harmonic motion. Therefore, the motion of the particle cannot be classified as SHM.
5. Determine the Motion Characteristics: Since the particle does not exhibit SHM, we can conclude:
- The displacement of the particle will not be in SHM.
- The velocity of the particle will not be in SHM.
- The acceleration of the particle will not be in SHM.
6. Final Answer: The correct answer is "none of the above" as the particle does not exhibit simple harmonic motion in any of the aspects mentioned.
F=t2−kx
where k is a constant, x is the displacement, and t is time.
F=−kx
This means that the force should only depend on the displacement x and not on time t.
- The displacement of the particle will not be in SHM.
- The velocity of the particle will not be in SHM.
- The acceleration of the particle will not be in SHM.
Topper's Solved these Questions
Similar Questions
A particle of mass 4 kg is acted upon by steady force of 4 N.Distance travelled by the particle in 4 sec is
View SolutionA particle of unknown mass is acted upon by a force →F=(100e−2tˆi)N. If at t = 0.00 s the particle is at rest, for the time interval t=0.00 s to t= 2.00 s find (a) the impulse on the particle and (b) the average force on the particle.
View Solution
Knowledge Check
A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
A2 FtmB2FtmCFtmDF2t22mA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
AF2t2mBF2t22mCF2t23mDFt2mA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
AF2t2mBF2t22mCF2t23mDFt2m
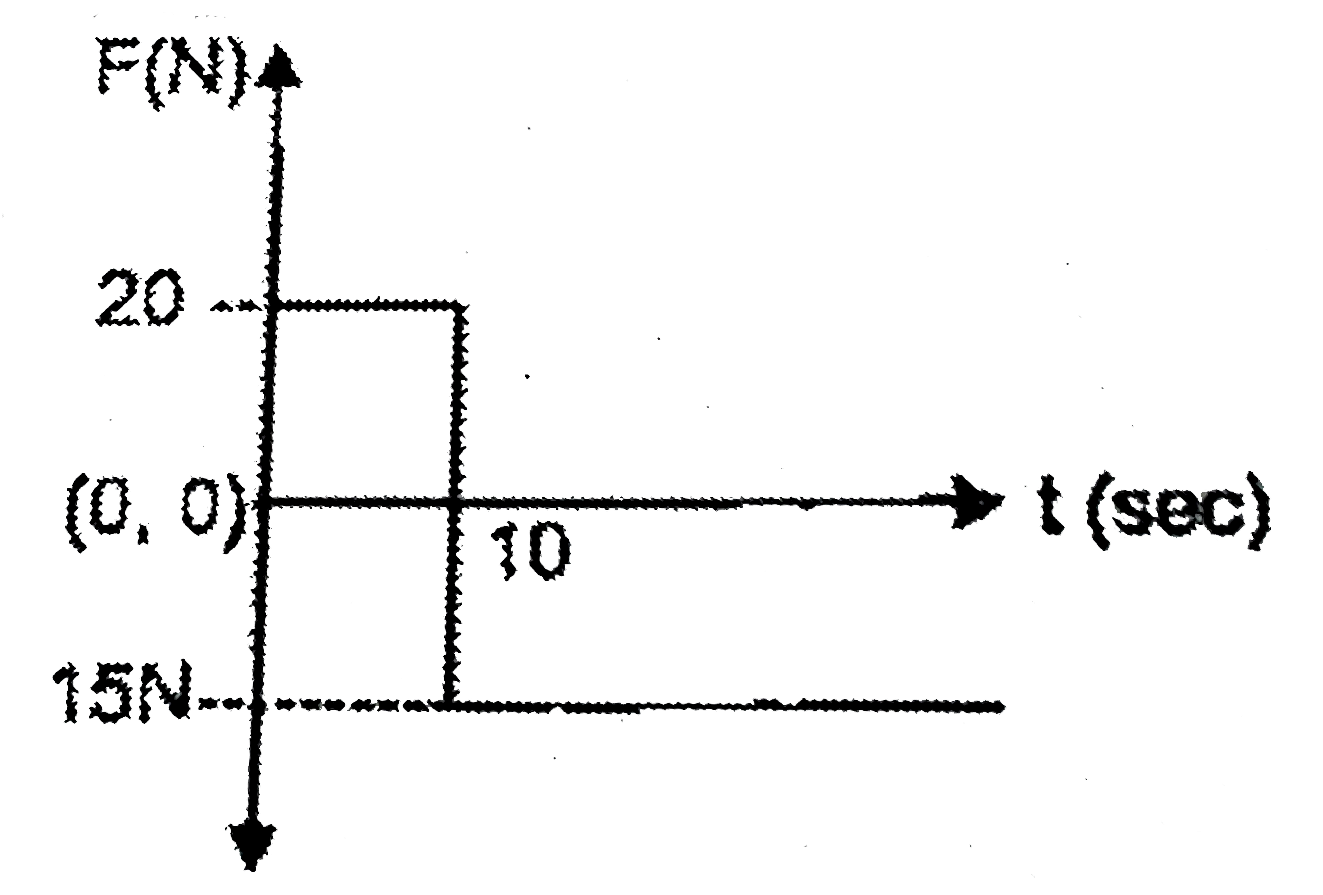
A particle of mass 10 kg is acted upon by a force F along the line of motion which varies as shown in the figure. The initial velocity of the particle is 10ms−1. Find the maximµm velocity attained by the particle before it comes to instantaneous rest.
View SolutionA particle of mass m is acted upon by a force F given by the emprical law F=Rt2υ(t)
If this law is to be tested experimentally by observing the motion starting from rest, the best way is to plot :
View SolutionA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
View SolutionA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
View SolutionA particle of mass m is acted on by two forces of equal magnitude F maintaining their orientation relative to the velocity v as shown in Fig. The momentum of the particle

View Solution
