A sphere of mass m is rolling without sliding along positive x-axis on a rough horizontal surface of coefficient of friction μ. It elastically collides with a wall and then returns. The correct statement of frictional force (f) acting on the sphere is
f=μmgˆi before collision and f=μmgˆi after collision
f=0 before collision and f=+μmgˆi after collision
f<μmgˆi before collision and f=μmgˆi after collision
f=μmgˆi before collision and just after collision
The correct Answer is:B
To solve the problem regarding the frictional force acting on a sphere of mass m that is rolling without sliding and collides elastically with a wall, we can break down the situation into steps.
1. Understanding Initial Conditions:
- The sphere is rolling without sliding along the positive x-axis. This means that the velocity of the center of mass v and the angular velocity ω are related by the equation v=Rω, where R is the radius of the sphere.
2. Collision with the Wall:
- When the sphere collides elastically with the wall, it will reverse its linear velocity. If the initial velocity before collision is v, after the collision, the velocity will become −v (assuming the wall is perfectly rigid and the collision is perfectly elastic).
3. Friction Before Collision:
- Before the collision, since the sphere is rolling without sliding, the frictional force acting on the sphere is zero. This is because there is no relative motion between the sphere and the surface at the point of contact.
4. Friction After Collision:
- After the collision, the sphere will try to continue moving in the negative x-direction. However, due to the nature of rolling without sliding, the frictional force will act in the direction opposite to the motion of the center of mass (which is now moving left).
- This means that the frictional force will act to the right (positive x-direction) to prevent slipping and to maintain rolling motion.
5. Direction of Frictional Force:
- The frictional force acts to the right after the collision because it needs to provide the necessary torque to keep the sphere rolling in the correct direction. The angular velocity ω remains the same in magnitude but changes direction due to the collision.
Conclusion:
- The correct statement regarding the frictional force acting on the sphere is that before the collision, the frictional force is zero, and after the collision, the frictional force acts in the positive x-direction.
- The sphere is rolling without sliding along the positive x-axis. This means that the velocity of the center of mass v and the angular velocity ω are related by the equation v=Rω, where R is the radius of the sphere.
- When the sphere collides elastically with the wall, it will reverse its linear velocity. If the initial velocity before collision is v, after the collision, the velocity will become −v (assuming the wall is perfectly rigid and the collision is perfectly elastic).
- Before the collision, since the sphere is rolling without sliding, the frictional force acting on the sphere is zero. This is because there is no relative motion between the sphere and the surface at the point of contact.
- After the collision, the sphere will try to continue moving in the negative x-direction. However, due to the nature of rolling without sliding, the frictional force will act in the direction opposite to the motion of the center of mass (which is now moving left).
- This means that the frictional force will act to the right (positive x-direction) to prevent slipping and to maintain rolling motion.
- The frictional force acts to the right after the collision because it needs to provide the necessary torque to keep the sphere rolling in the correct direction. The angular velocity ω remains the same in magnitude but changes direction due to the collision.
- The correct statement regarding the frictional force acting on the sphere is that before the collision, the frictional force is zero, and after the collision, the frictional force acts in the positive x-direction.
Topper's Solved these Questions
Similar Questions

A solid sphere is rolling purely on a rough horizontal surface (coefficient of kinetic friction =μ) with speed of centre =u. It collides in-elastically with a smooth vertical wall at a certain moment, the coefficient of restituting being 12. The sphere will begin pure rolling after a time.View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of weight W is kept on a rough horizontal surface (friction coefficient μ). Two forces W/2 each are applied as shown in the choose the correct statement
 .AFor μ>√35 block will move .BFor μ<√35, work done by frictional force is zero in ground frame .CFor μ>√32 frictional force will do positive work (in ground frame) .DFor μ≤√32 block will move .
.AFor μ>√35 block will move .BFor μ<√35, work done by frictional force is zero in ground frame .CFor μ>√32 frictional force will do positive work (in ground frame) .DFor μ≤√32 block will move . - Question 2 - Select One
A particle of mass m is given a velocity u on a rough horizontal surface of friction coefficient μ. The average power imparted by friction until it stops is
AzeroB12μmguCμmguD2μmgu - Question 3 - Select One
A massless string is wrapped around a hollow cylinder having mass m and radius r. The cylinder is kept on a rough horizontal surface (coefficient of friction is μ). A constant force F is applied as shown in the figure. In case of pure rolling, the friction force acting on the bottom most point of the cylinder is
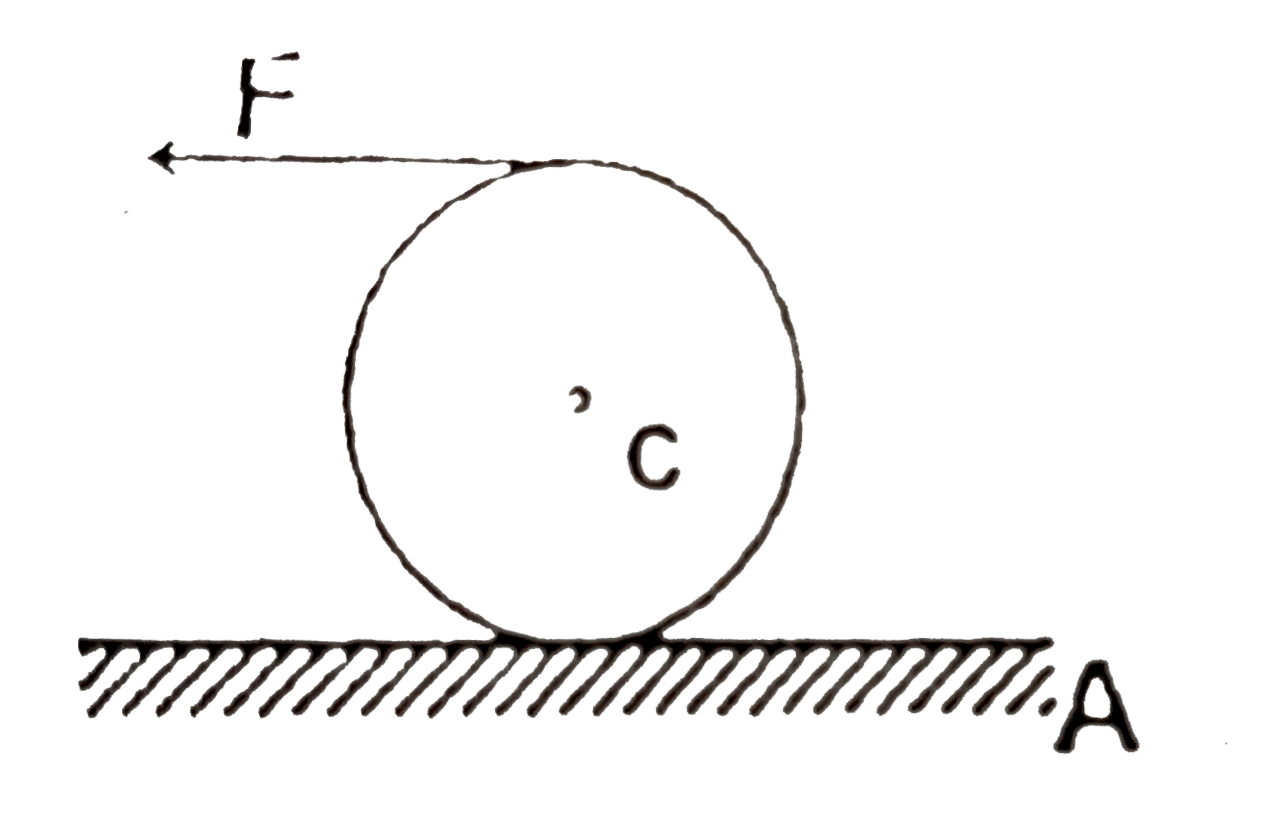 AzeroBμmgCμmg/2D3μmg/2
AzeroBμmgCμmg/2D3μmg/2
A solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 View Solution
View SolutionA solid sphere of mass 10kg is placed on a rough surface having coefficient of friction μ=0.1. A constant force F=7N is applied along a line passing through the centre of the sphere as shown in the figure. The value of frictional force on the sphere is.
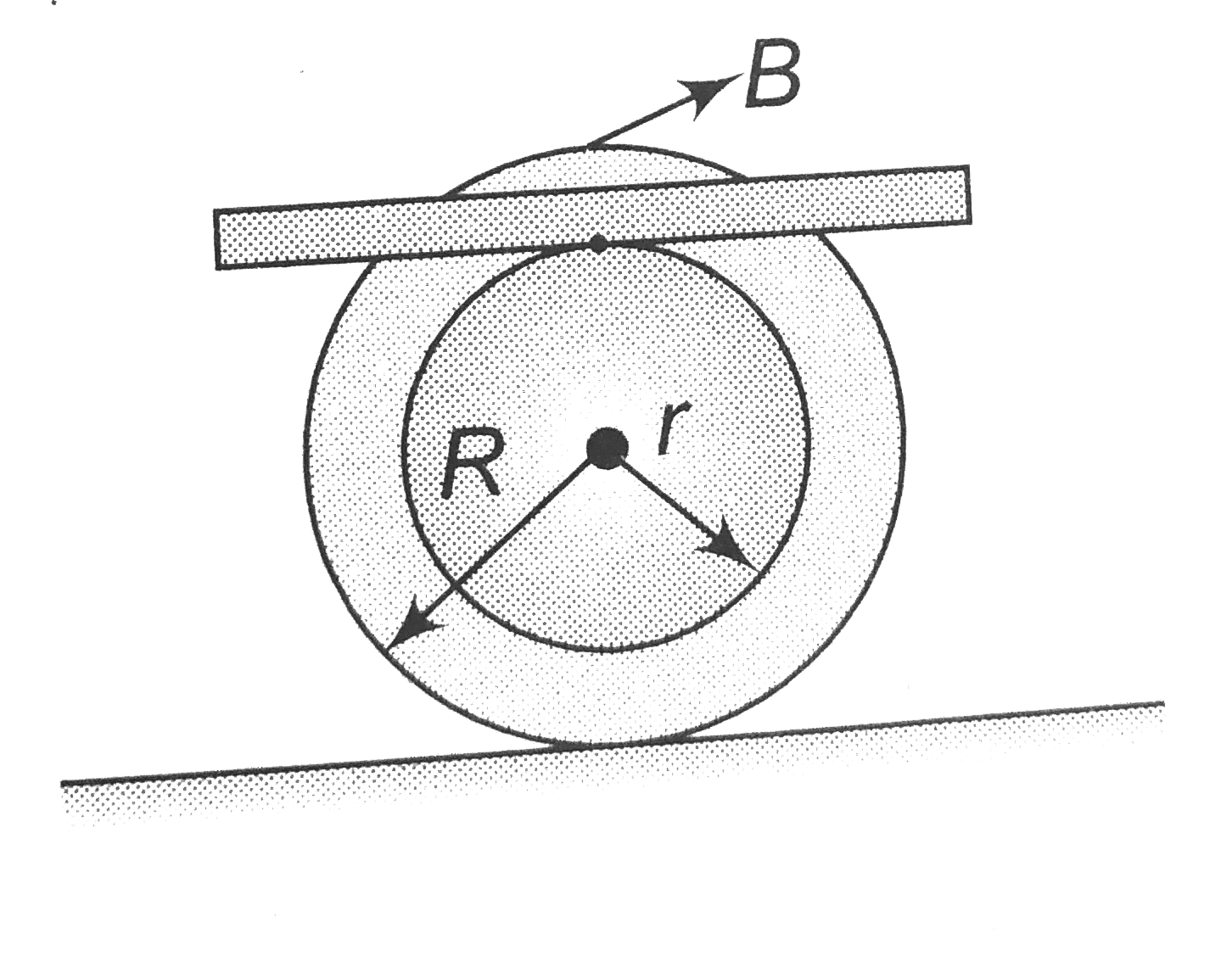 .View Solution
.View SolutionA uniform solid sphere A of mass m is rolling without sliding on a a smooth horizontal surface. It collides elastically and head - on with another stationary hollow sphere B of the same mass and radius. Assuming friction to be absent everywhere, the ratio of the kinetic energy of B to that of A just after the collision is
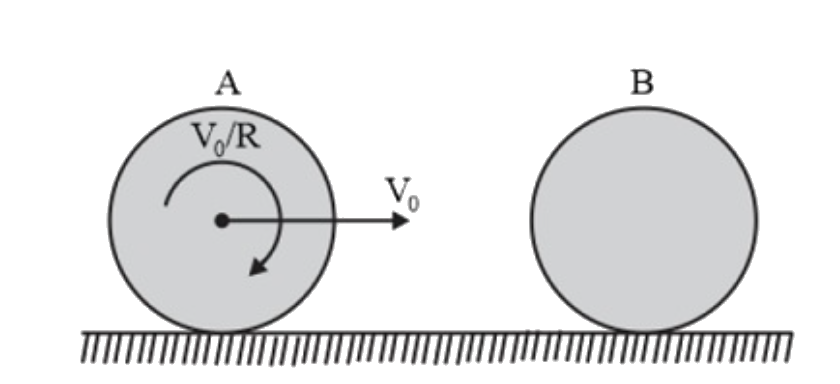 View Solution
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
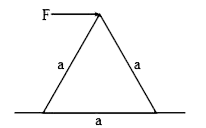 View Solution
View Solution

