Two long parallel wires placed 0.08 m apart, carry currents 3 A and 5 A in the same direction. what is the distance from the conductor carrying the larger current to the point where the resultant magnetic field is zero?
0.5 m
0.04 m
0.05 m
0.4m
The correct Answer is:C
To solve the problem, we need to find the distance from the wire carrying the larger current (5 A) to the point where the resultant magnetic field is zero. We will denote the distance from the wire carrying the larger current as x and the distance from the wire carrying the smaller current (3 A) will then be 0.08−x meters.
1. Identify the Magnetic Field Due to Each Wire:
The magnetic field B due to a long straight wire carrying current I at a distance r is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
2. Set Up the Magnetic Fields:
- For the wire carrying 3 A (let's call it Wire 1), the magnetic field at point P (where the resultant field is zero) is:
B1=μ0⋅32π(0.08−x)
- For the wire carrying 5 A (Wire 2), the magnetic field at point P is:
B2=μ0⋅52πx
3. Determine the Direction of the Magnetic Fields:
Since both currents are in the same direction, the magnetic field due to Wire 1 (3 A) will be directed downwards, and the magnetic field due to Wire 2 (5 A) will be directed upwards. Therefore, we can set up the equation for the point where the magnetic fields cancel each other out:
B1=B2
4. Set Up the Equation:
From the above, we have:
μ0⋅32π(0.08−x)=μ0⋅52πx
We can cancel μ0 and 2π from both sides:
30.08−x=5x
5. Cross Multiply to Solve for x:
Cross multiplying gives:
3x=5(0.08−x)
Expanding the right side:
3x=0.4−5x
6. Combine Like Terms:
Adding 5x to both sides:
3x+5x=0.4
8x=0.4
7. Solve for x:
Dividing both sides by 8:
x=0.48=0.05 m
Conclusion:
The distance from the conductor carrying the larger current (5 A) to the point where the resultant magnetic field is zero is 0.05 m.
The magnetic field B due to a long straight wire carrying current I at a distance r is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
- For the wire carrying 3 A (let's call it Wire 1), the magnetic field at point P (where the resultant field is zero) is:
B1=μ0⋅32π(0.08−x)
- For the wire carrying 5 A (Wire 2), the magnetic field at point P is:
B2=μ0⋅52πx
Since both currents are in the same direction, the magnetic field due to Wire 1 (3 A) will be directed downwards, and the magnetic field due to Wire 2 (5 A) will be directed upwards. Therefore, we can set up the equation for the point where the magnetic fields cancel each other out:
B1=B2
From the above, we have:
μ0⋅32π(0.08−x)=μ0⋅52πx
We can cancel μ0 and 2π from both sides:
30.08−x=5x
Cross multiplying gives:
3x=5(0.08−x)
Expanding the right side:
3x=0.4−5x
Adding 5x to both sides:
3x+5x=0.4
8x=0.4
Dividing both sides by 8:
x=0.48=0.05 m
The distance from the conductor carrying the larger current (5 A) to the point where the resultant magnetic field is zero is 0.05 m.
Topper's Solved these Questions
Similar Questions
Two parallel wires P and Q placed distance r apart. They are carrying currents I1 and I2 where I1>I2, but in opposite directions as shown in figure. Find the point on the line PQ where the resultant magnetic field is zero.
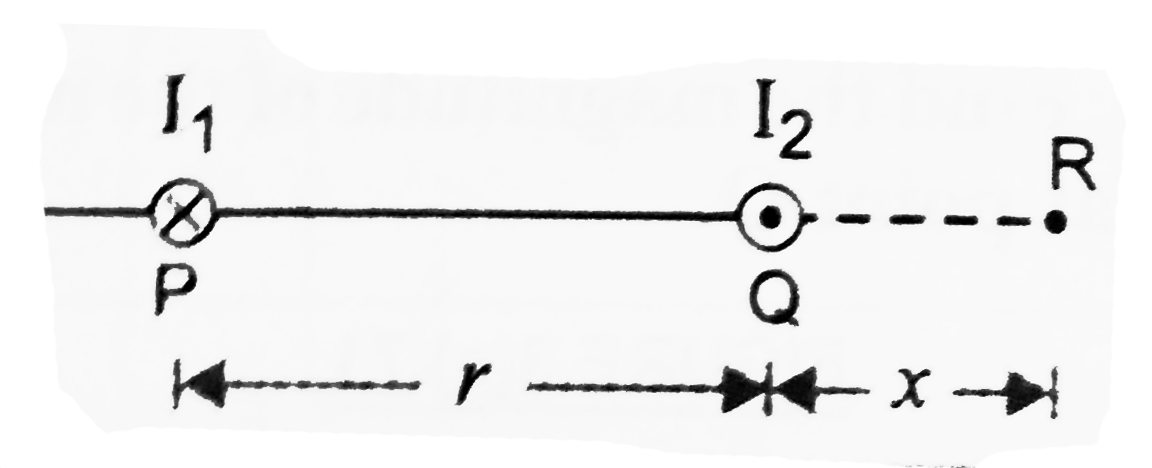
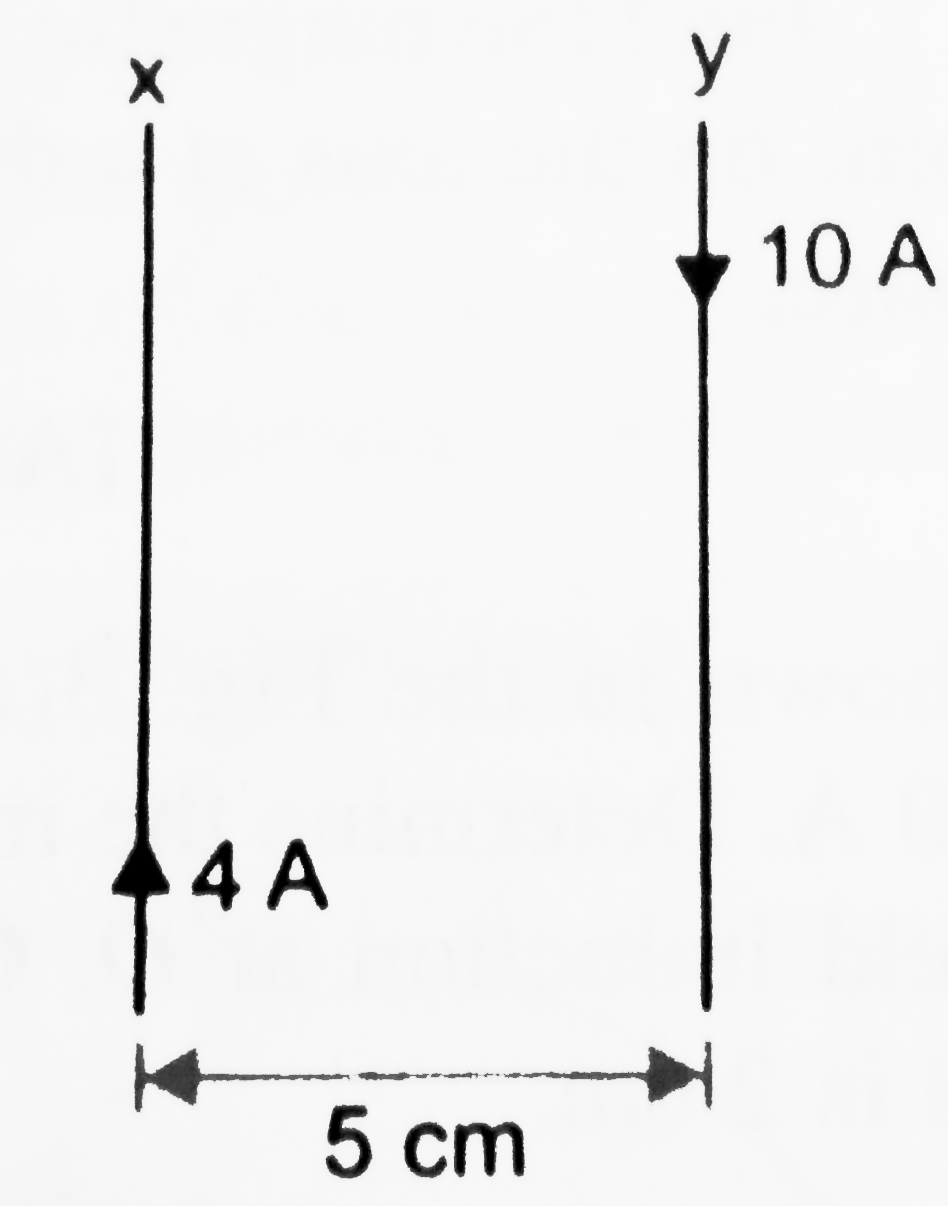
View SolutionFigure shows two long parallel straight wires distance 5cm apart carrying currents 4A and 10A in opposite directions. Find the position of a point where the resultant magnetic field due to current in two wires in zero.
View Solution
Knowledge Check
Two thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
Arepel each other with a force of μ0i2/(2πd)Battract each other with a force of μ0i2/(2πd)Crepel each other with a force of μ0i2/(2πd2)Dattract each other with a force of μ0i2/(2πd2)Two long parallel wires are at a distance of 4 cm. They carry currents I and 31 in same direction. Where will the field produced by both wires be zero from current I?
A0.02 cmB0.01 cmC1 cmD3 cmTwo long and parallel straight wires A and B carrying currents of 0.8 A and 5.0 A in the same direction are separated by distance of 0.4 cm. What is the force on a 10 cm section of wire A ?
A10−5NB2×10−5NC3×10−5ND4×10−5N
Let two long parallel wires, a distance d apart, carry equal currents I in the same direction. One wires at x=0, the other at x=d (as shown in Fig) Determine magnetic field at any point x-axis between the wires as a function of x.

View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
View SolutionVariation of magnetic field with distance from current carrying conductor is:
View SolutionTwo parallel conductors A and B separated by 5cm carry electric current of 6A and 2A in the same direction. The point between A and B where the field is zero at
View Solution
