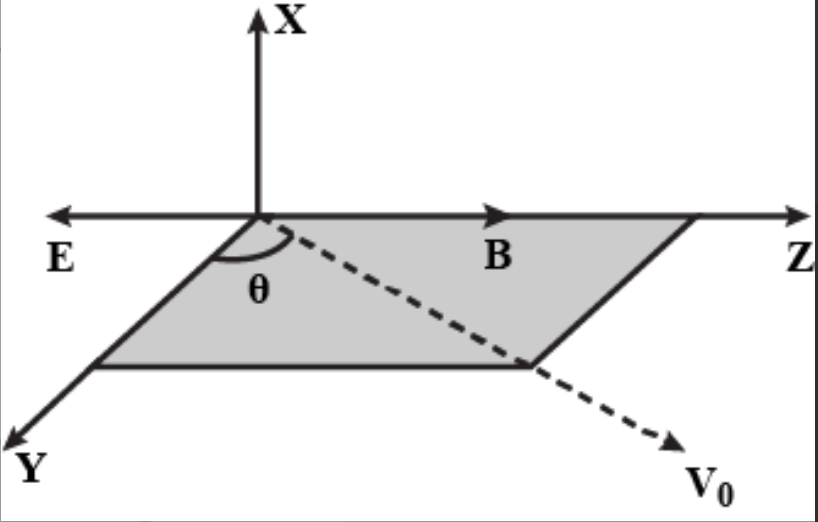
In a certain region uniform electric field E and magnetic field B are present in mutually opposite directions. At the instant , a particle of mass m carrying a charge q is given velocity at angle , with the axis, in the yz plane. The time after which the speed of the particle would be minimum is equal to
The correct Answer is:C
Step by step video, text & image solution for In a certain region uniform electric field E and magnetic field B are present in mutually opposite directions. At the instant t=0, a particle of mass m carrying a charge q is given velocity v_(0) at angle theta, with the y- axis, in the yz plane. The time after which the speed of the particle would be minimum is equal to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
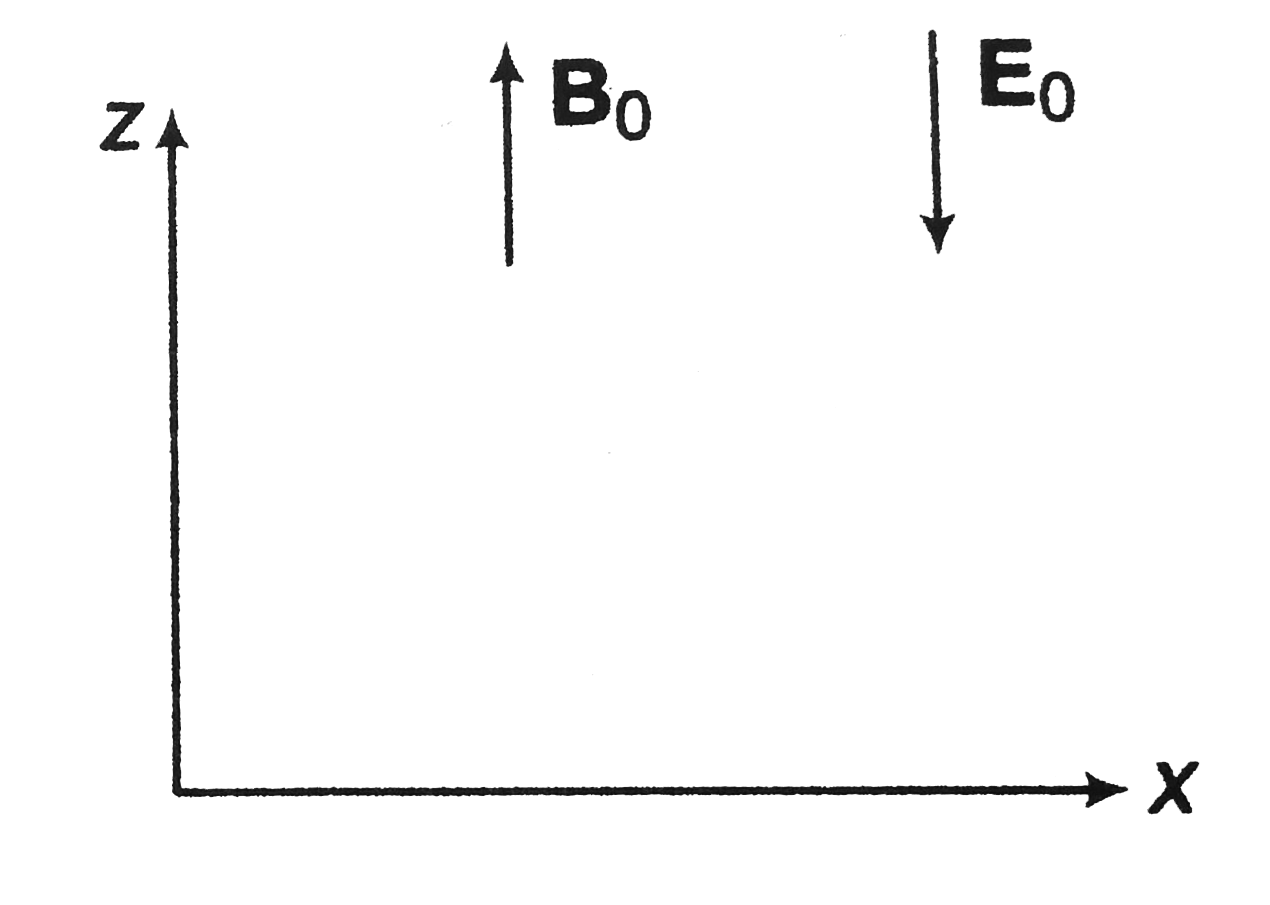
In a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass in and charge q is given a velocity v=v−0ˆj+v−0ˆk. Find the minimum speed of the particle and the time when it happens so.
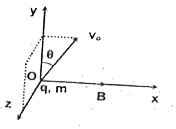
View SolutionA particle of mass m and charge q is lying at the origin in a uniform magnetic field B directed along x-axis. At time t = 0, it is given a velocity v0, at an angleθ with the y-axis in the xy-plane. Find the coordinates of the particle after one revolution.
View Solution
Knowledge Check
In a certain region uniform electric field E and magnetic field B are present in mutually opposite directions. At the instant t=0, a particle of mass m carrying a charge q is given velocity v0 at angle θ, with the y− axis, in the yz plane. The time after which the speed of the particle would be minimum is equal to
AmV0qEBmV0sinθqECmV0cosθqED2πmqBA particle of mass m, carrying a charge q, is lying at the origin in a uniform magentic field directed along X axis. At the instant t = 0 it is given a velocity va at an angle θ with the y-axis, in the XY plane. The coordinates of the particle after two revolution will be
A(0,02πmv0sinθqB)B(2πmv0sinθqB,0,0)C(4πmv0sinθqB,0,0)D(0,0,0)A charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
AmvsinθqBBmvqBsinθCmvqBDmvtanθqB
In a region of space, both electric and magnetic field are present simultaneously in opposite direction. A positively charged particle is projected with certain speed an angle θ(<90∘) with magnetic field. It will move in a
View SolutionA uniform electric field →E in the y-direction and uniform magnetic field →B in the x-direction exists in free space. A particle of mass m and carrying charge g is projected from the origin with speed v0 along the y axis. The speed of the particle as a function of its y coordinate will be
View SolutionA particle with mass m and positive charge q released from rest at the origin as shown in figure. There is a uniform electric field E0in +y direction and uniform magnetic field B0 directed out of the page. The path of the particle as shown is called cycloid. The particle always moves in x−y plane. The velocity at any time t after the start is given as
The time for which the y− coordinate of the particle bomes maximum for the first time is
View SolutionA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
z-coordinate of the particle as a function of time after the magnetic field is switched on is
View Solution