In an experiment on the photoelectric effect , the slope of the cut - off voltage versus frequency of incident light is found to be 4.12×10−15V s . The value of Planck's constant is
6.592×10−34 J s
6.592×10−31 J s
9.592×10−34 J s
6.592×10−30 J s
The correct Answer is:A
To find the value of Planck's constant (h) using the slope of the cut-off voltage versus frequency in the photoelectric effect experiment, we can follow these steps:
1. Understand the relationship: In the photoelectric effect, the maximum kinetic energy (KE_max) of the emitted electrons is given by the equation:
KEmax=hν−ϕ
where ν is the frequency of the incident light, h is Planck's constant, and ϕ is the work function of the material.
2. Relate cut-off voltage to energy: The cut-off voltage (V0) can be expressed in terms of kinetic energy:
KEmax=eV0
where e is the charge of an electron. Therefore, we can rewrite the equation as:
eV0=hν−ϕ
3. Rearranging the equation: Rearranging the above equation gives:
V0=heν−ϕe
This is in the form of a linear equation y=mx+c, where:
- y=V0 (cut-off voltage)
- x=ν (frequency)
- m=he (slope)
- c=−ϕe (y-intercept)
4. Identify the slope: From the problem, we know that the slope m is given as:
m=4.12×10−15V s
Thus, we have:
he=4.12×10−15V s
5. Calculate Planck's constant: To find h, we need to multiply the slope by the charge of the electron e:
h=m⋅e
The charge of the electron e is approximately:
e=1.6×10−19C
Therefore:
h=(4.12×10−15V s)×(1.6×10−19C)
6. Perform the multiplication:
h=4.12×1.6×10−15×10−19=6.592×10−34J s
Final Result:
The value of Planck's constant h is:
h≈6.592×10−34J s
KEmax=hν−ϕ
where ν is the frequency of the incident light, h is Planck's constant, and ϕ is the work function of the material.
KEmax=eV0
where e is the charge of an electron. Therefore, we can rewrite the equation as:
eV0=hν−ϕ
V0=heν−ϕe
This is in the form of a linear equation y=mx+c, where:
- y=V0 (cut-off voltage)
- x=ν (frequency)
- m=he (slope)
- c=−ϕe (y-intercept)
m=4.12×10−15V s
Thus, we have:
he=4.12×10−15V s
h=m⋅e
The charge of the electron e is approximately:
e=1.6×10−19C
Therefore:
h=(4.12×10−15V s)×(1.6×10−19C)
h=4.12×1.6×10−15×10−19=6.592×10−34J s
The value of Planck's constant h is:
h≈6.592×10−34J s
Topper's Solved these Questions
Similar Questions
In an experiment on photoelectric effect, the slope of the cut-offf voltage versus frequency of incident light is found to be 4.12×10−15V s. calculate the value of Planck's constant.
View SolutionIn an experiment on photoelectric effect, the slope of the cut off voltage versus frequency of incident light is found to be 4.12×10−15Vs. Given e=1.6×10−19C, estimate the value of Planck's constant.
View Solution
Knowledge Check
In photoelectric effect the slope of stop of stopping potential versus frequency of incident light for a given surface will be
Ahe−1Be hCeDhFor a photoelectric cell, the graph shown the variation of cut off voltage (V0) with frequency (v) of incident light is
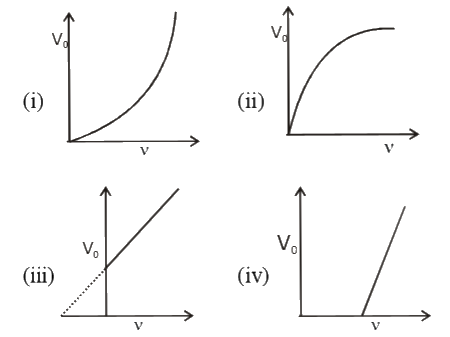 A(i)B(ii)C(iii)D(iv)
A(i)B(ii)C(iii)D(iv)In photo electric effect, the slope of the straight line graph between stopping potential and frequency of the incident light gives the ratio of Planck's constant to
Acharge of electronBwork functionCphoto electric currentDK.E. of electron
In photoelectric effect the slope of straight line graph between stopping potential (Vs) and frequency of incident light (v) gives

View SolutionFor a photoelectric cell the graph showing the variation of cut of voltage (V) with frequency (v) of incident light is best represented by
View SolutionIn photoelectric effect the slope of straight line graph between stopping potential (V0) and freqency of incident light (v) gives:
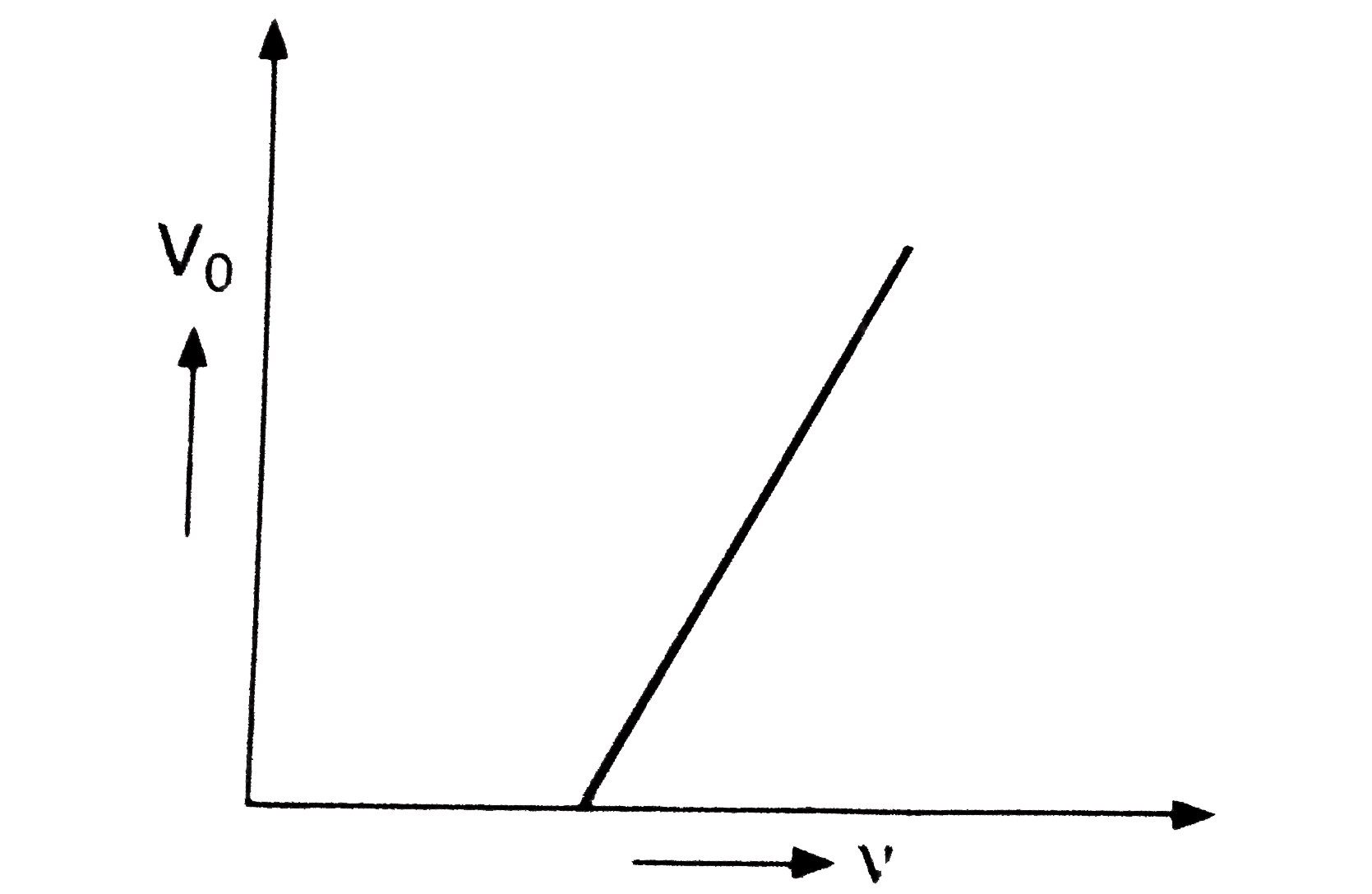
View SolutionFor a photoelectric cell the graph showing the variation of cut of voltage (V0) with frequency (v) of incident light is best represented by

View Solution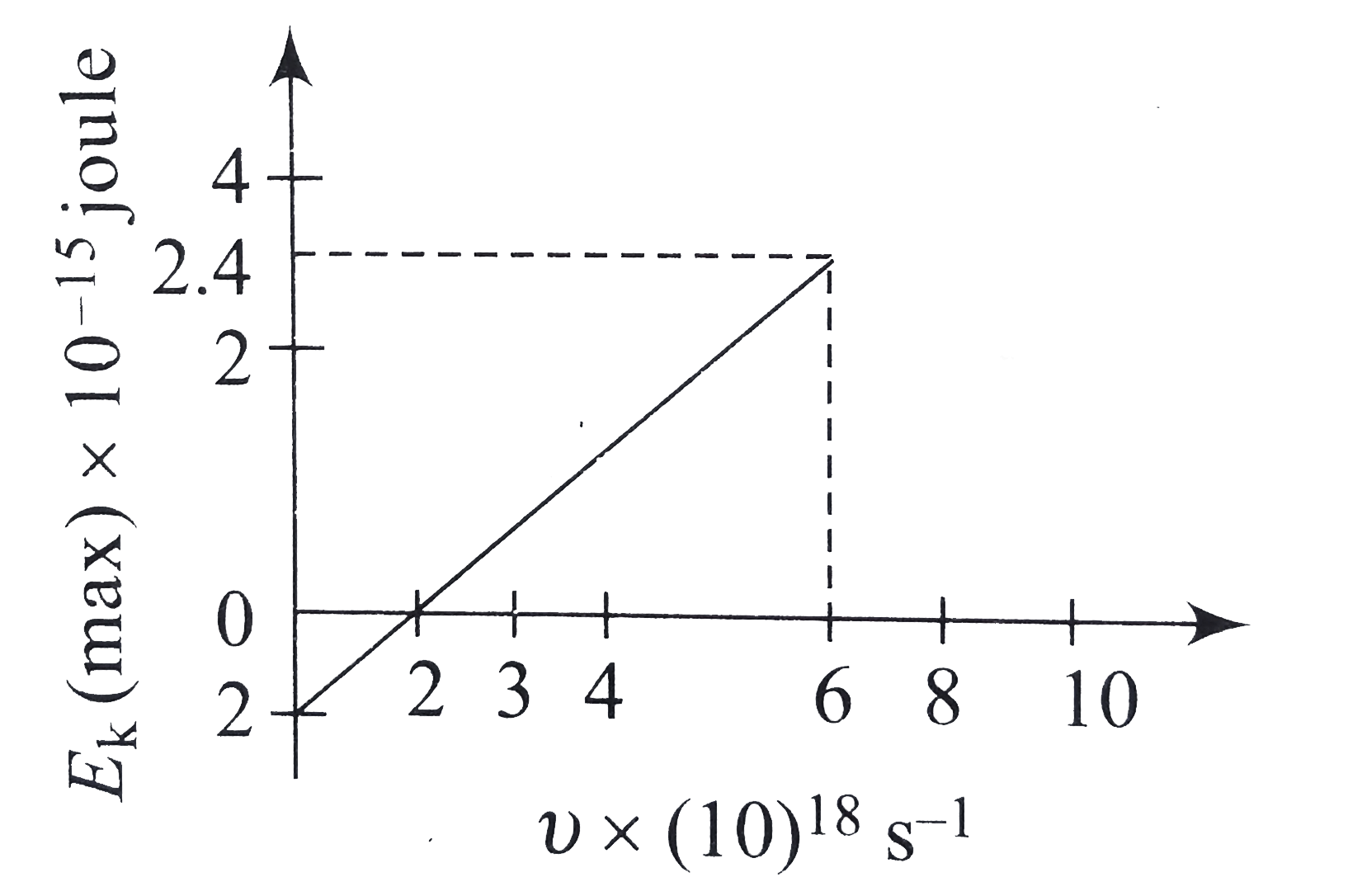
In the experiment on photoelectric effect, the graph between EK(max) and v is found to be a straight line as sshoen in fig. The threshold frequency and Planck's constant according to this graph are
View Solution
