Let ABCD is a rectangle whose sides given area a and b. A rectangle PQRS whose area is A is shown in figure, then
Area A is maximum when θ=π3
area A is maximum when θ=π4
maximum value of area A=14(a+b)2
maximum value of area A=12(a+b)2
The correct Answer is:B,D
Step by step video solution for Let ABCD is a rectangle whose sides given area a and b. A rectangle PQRS whose area is A is shown in figure, then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREABOOK - FIITJEECHAPTER - AREAEXERCISE - Comprehensions
9 Videos
- AREABOOK - FIITJEECHAPTER - AREAEXERCISE - Match the columns
3 Videos
- AREABOOK - FIITJEECHAPTER - AREAEXERCISE - Assignment Problems (Objective) Level - I
49 Videos
- APPLICATION OF DERIVATIVEBOOK - FIITJEECHAPTER - APPLICATION OF DERIVATIVEEXERCISE - Numerical
3 Videos
- CIRCLEBOOK - FIITJEECHAPTER - CIRCLEEXERCISE - Numerical Based
2 Videos
Similar Questions
Knowledge Check
ABCD is a rectangle of dimensions 8 units and 6 units AEFC is a rectangle drawn in such a way that diagonal AC of the first rectangle is one side and side opposite to it is touching the first rectangle at D as shown in the figure. What is the ratio of the area of rectangle ABCD to that of AEFC ?
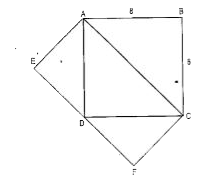 A2B3/2C1D8/9
A2B3/2C1D8/9Maximum area of a rectangle whose perimeter is given as 24 metres is equal to
A36m2B49m2C64m2D81m2The area of a rectangle will be maximum for the given perimeter, when rectangle is a
AparallelogramBtrapeziumCsquareDnone of these
Find the areas of the rectangles whose sides are :
3 cm and 4 cm
View SolutionFind the areas of the rectangles whose sides are :
2km and 3 km
View SolutionFind the areas of the rectangles whose sides are :
12 m and 21 m
View Solution(i) The two sides of a rectangle are x units and (10 - x) units. For what value of x, the area of rectangle will be maximum?
(ii) Prove that a rectangle, whose area is constant has minimum perimeter if it is a square.
View SolutionA rectangle whose adjacent sides are equal becomes a __________.
View Solution
