Let A and D be opposite vertices of a square. A frog starts jumping at vertex A. From any vertex of the square except D, it may jump to either of the two adjacent vertices. When it reaches D, the from stop and stays there. The number of distinct path of exactly 6 jumps ending at D are ____________________
The correct Answer is:2
Topper's Solved these Questions
- PERMUTATIONS & COMBINATIONSBOOK - FIITJEECHAPTER - PERMUTATIONS & COMBINATIONSEXERCISE - EXERCISE 3
3 Videos
- PERMUTATIONS & COMBINATIONSBOOK - FIITJEECHAPTER - PERMUTATIONS & COMBINATIONSEXERCISE - EXERCISE 4
2 Videos
- PERMUTATIONS & COMBINATIONSBOOK - FIITJEECHAPTER - PERMUTATIONS & COMBINATIONSEXERCISE - NUMERICAL BASED
3 Videos
- PARABOLABOOK - FIITJEECHAPTER - PARABOLAEXERCISE - NUMERICAL BASED
5 Videos
- PROBABILITYBOOK - FIITJEECHAPTER - PROBABILITYEXERCISE - Exercise 7
2 Videos
Similar Questions
A circle of radius 5 cm passes through two adjacent vertices of a square. A tangent to circle drawn from 3rd vertex of the square is twice of the length of the side of the square. The side of the square is
View SolutionAn ant is situated at the vertex A of the triangle ABC. Every movement of the ant consists of moving to one of other two adjacent vertices from the vertex where it is situated. The probability of going to any of the other two adjacent vertices of the triangle is equal. The probability that at the end of the fourth movement the ant will be back to the vertex A, is:
View Solution
Knowledge Check
Four identical mirror are made to stand vertically to form a square arrangement as shown in a top view. A ray starts from the midpoint M of mirror AD and after two reflections reaches corner D. Then, angle θ must be
 Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)
Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)Four identical mirror are made to stand vertically to form a square arrangement as shown in a top view. A ray starts from the midpoint M of mirror AD and after two reflections reaches corner D. Then, angle θ must be
 Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)
Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)Four indentical mirrors are made to stand vertically to form a square arrangement as shown in a top view. A ray starts from the midpoint M of mirror AD and after two reflections reaches corner D. Then, angle θ must be
 Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)
Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)
Show that A (3, 2), B (6, -2) and C (2, -5) can be the vertices of a square.
Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.
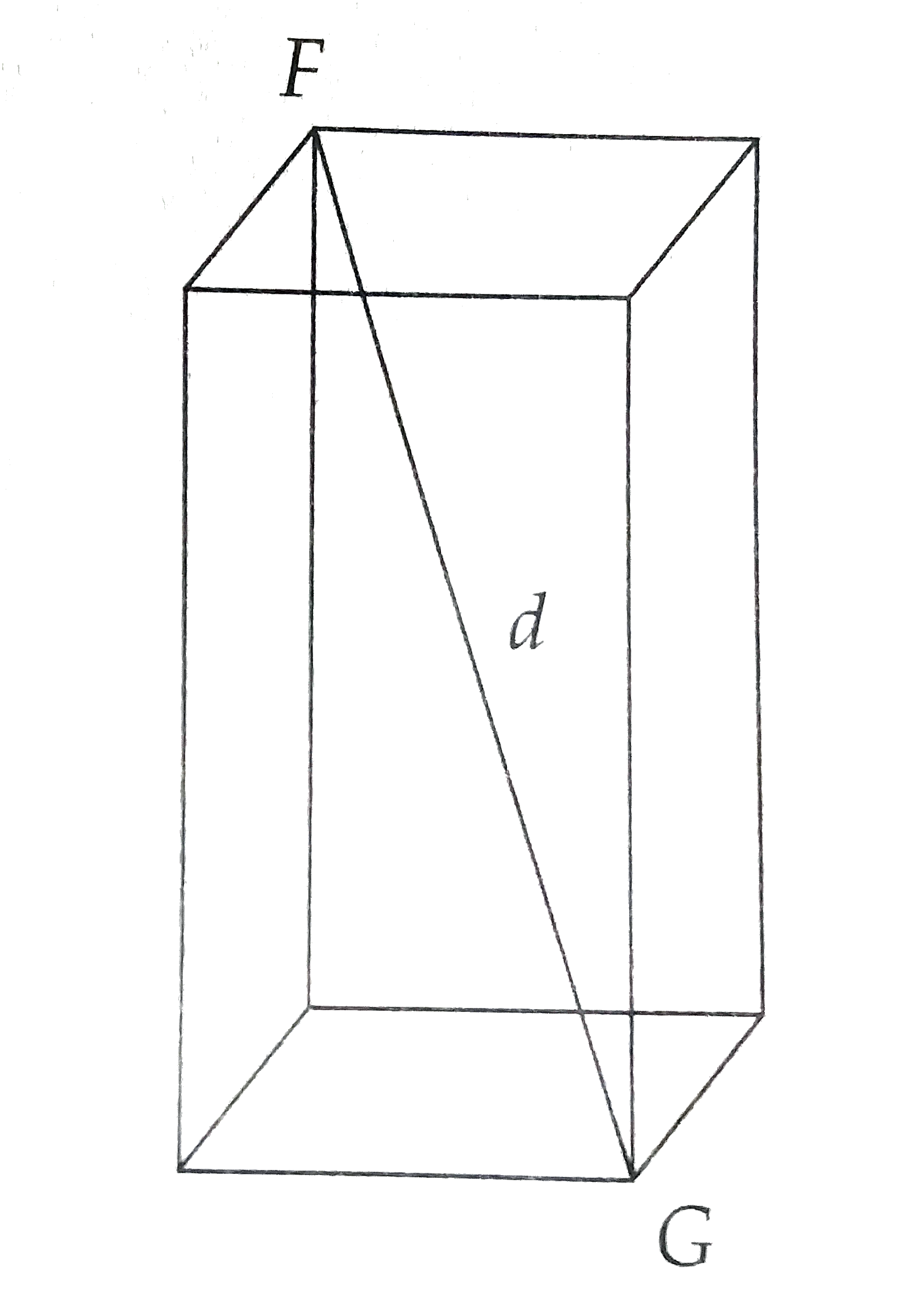
View SolutionD is the distance from vertex F to vertex G. The base is square, and the height is twice the width. What is the volume of the solid in terms of d ?
View SolutionA (-2,4) , C (4,10) and D (-2,10) are the vertices of a square ABCD. Use the graphical method to find ordinates of the fourth vertex B. Also, find:
The co ordinates of the point of intersection of the diagonals of the square ABCD.
View SolutionA (-2,4) , C (4,10) and D (-2,10) are the vertices of a square ABCD. Use the graphical method to find ordinates of the fourth vertex B. Also, find:
The co ordinates of the mid point of CD.
View SolutionShow that A (3, 2), B (6, -2) and C (2, -5) can be the vertices of a square.
Find the co-ordinates of its fourth vertex D, if ABCD is a square.
View Solution
