Prove that a sequence in an A.P., if the sum of its n terms is of the form An2+Bn,whereA,B are constants.
To prove that a sequence is an Arithmetic Progression (A.P.) if the sum of its first n terms is of the form Sn=An2+Bn, where A and B are constants, we can follow these steps:
Step 1: Define the sum of the first n terms of an A.P.
Let the first term of the A.P. be a and the common difference be d. The sum of the first n terms Sn of an A.P. can be expressed as:
Sn=n2(2a+(n−1)d)
Step 2: Simplify the expression for Sn
We can simplify the expression for Sn:
Sn=n2(2a+nd−d)
=n2(2a−d+nd)
=n2((2a−d)+nd)
Step 3: Distribute n/2
Now, distribute n/2:
Sn=n(2a−d)2+n2d2
Step 4: Identify constants A and B
From the expression Sn=n2d2+n(2a−d)2, we can identify:
- A=d2
- B=2a−d2
Step 5: Conclusion
Since Sn can be expressed in the form An2+Bn where A and B are constants, we conclude that if the sum of the first n terms of a sequence is of the form An2+Bn, then the sequence is indeed an A.P.
Let the first term of the A.P. be a and the common difference be d. The sum of the first n terms Sn of an A.P. can be expressed as:
Sn=n2(2a+(n−1)d)
We can simplify the expression for Sn:
Sn=n2(2a+nd−d)
=n2(2a−d+nd)
=n2((2a−d)+nd)
Now, distribute n/2:
Sn=n(2a−d)2+n2d2
From the expression Sn=n2d2+n(2a−d)2, we can identify:
- A=d2
- B=2a−d2
Since Sn can be expressed in the form An2+Bn where A and B are constants, we conclude that if the sum of the first n terms of a sequence is of the form An2+Bn, then the sequence is indeed an A.P.
Similar Questions
Prove that a sequence in an A.P., if the sum of its n terms is of the form An2+Bn,whereA,B are constants.
View SolutionState 'T' for true and 'F' for false .
I. A sequence is an A.P ., if and only if the sum of its n terms is of the form An2+Bn , where A and B are constants .
II. If 18, a, b , −3 are in A.P., then a+b=15 .
III If a,c,b are in A.P., then 2c=a+b .
IV .The nth term from the end of an A.P. is the (m−n+1)th term from the beginning , where m terms are in A.P.
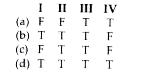
View Solution
Knowledge Check
If the sum of first n terms of an A.P. is 3n2−2n, then its 19th term is
A123B118C109D107
A sequence is an AP if the sum of its first n terms is of the form An2+Bn where A and B are constants independent of n .In such a case the common difference is 2A
View SolutionWrite the nth term of an A.P. the sum of whose n terms is Sn .
View SolutionIn an A.P., th e sum of its first n terms is 6n−n2. Find its 25th term.
View SolutionThe nth term of an A.P. is (5n-1). Find the sum of its 'n' terms.
View SolutionIf the nth term of an A.P. is (2n+1), find the sum of first n terms of the A.P.
View SolutionIf the sum of n terms of an A.P is 2n+3n2 , find the rth term
View SolutionIf the sum of n terms of an AP is n2−2n then find its nth term
View Solution
