Prove that sin−1(817)+sin−1(35)=sin−1(7785)
Video Solution
Text Solution
The correct Answer is:N/a
We have, sin−1'817+sin−1'35=sin−1'7785
∴LHS=sin−1'817+sin−1'35
=tan−1'815+tan−1'34
Let sin−1'817=θ1⇒sinθ1=817
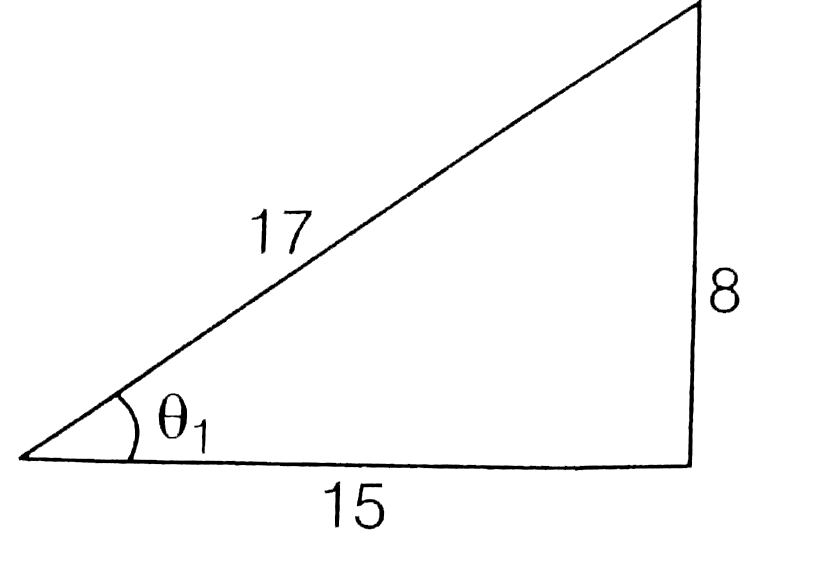
⇒tanθ1=815⇒θ1=tan−1'815
and sin−1'35=θ2⇒sinθ2=35
⇒tanθ2=34⇒θ2=tan−1'34
tan−1⎡⎣815+341−815×34⎤⎦,[∵tan−1x+tan−1y=tan−1'(x+y1−xy)]
=tan−1⎡⎢⎣32+456060−2460⎤⎥⎦=tan−1(7736)
Let θ3=tan−1'7736⇒tanθ3=7736
⇒sinθ3=77√5929+1296=7785
∴θ3=sin−1'7785
=sin−1'7785=RHS

Alternate Method
To prove, sin−1'817+sin−1'35=sin−1'7785
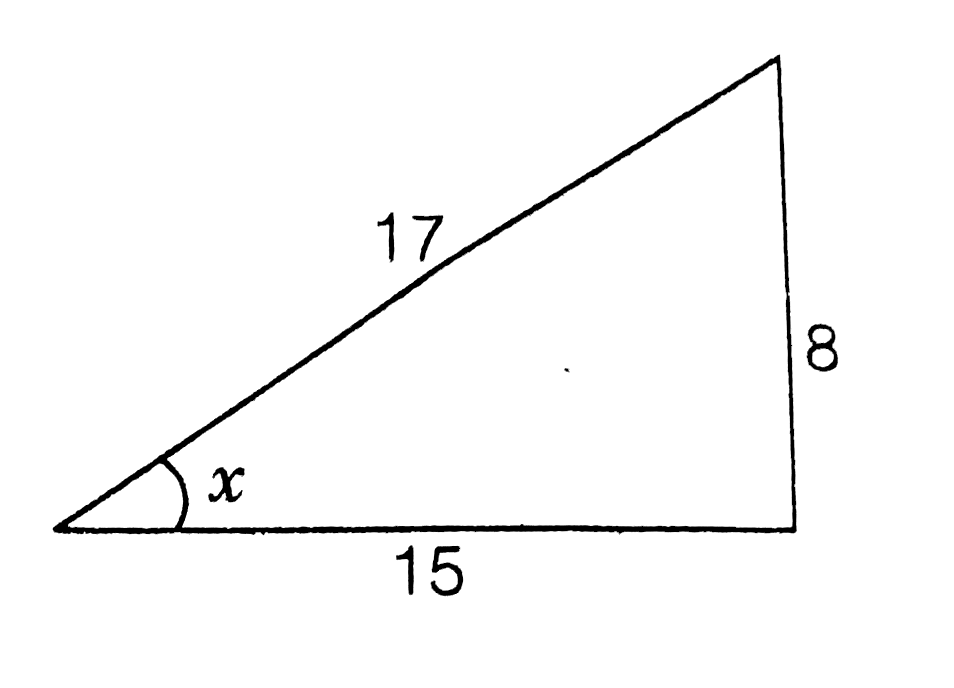
Let sin−1'817=x
rAsssinx=817
⇒cosx=√1−sin2θ=√1−(817)2
=√289−64289=√225289=1517
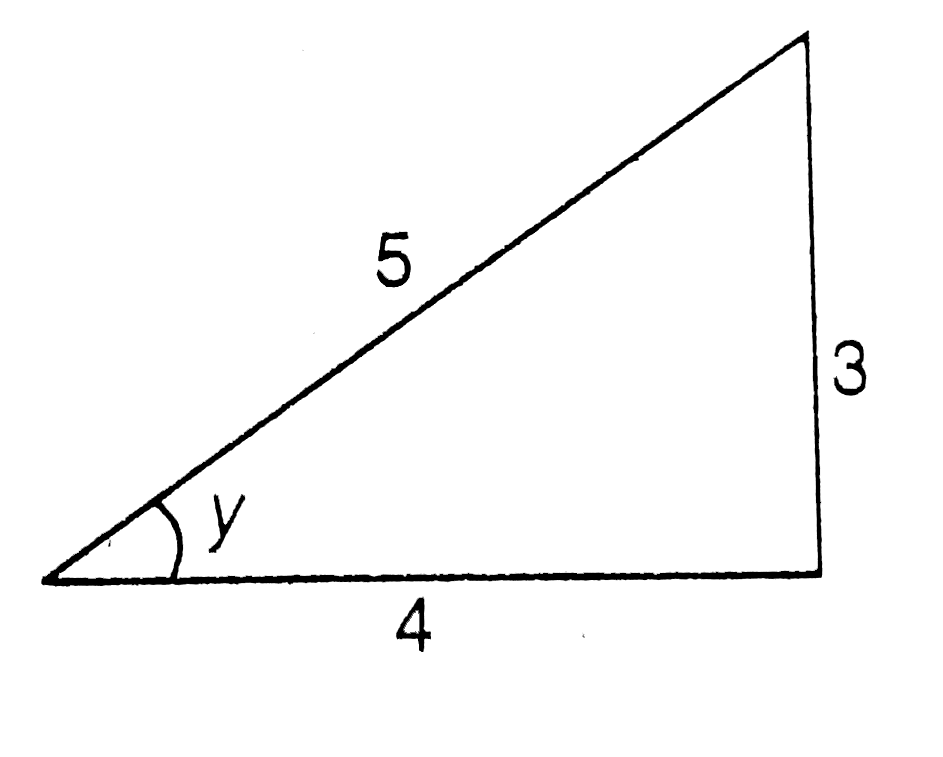
Let sin−1'35=y
⇒siny=35⇒sin2y=925
⇒cos2y=(45)2⇒cosy=45
Now, sin(x+y)=sinx.cosy+cosx.siny
=717.4/5+1517.3/5
=3285+4585=7785
⇒(x+y)=sin−1(7785)
⇒sin−1'817+sin−1'35=sin−1'7785
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Show that : sin−1(817)+sin−1(35)=sin−1(7785)
View SolutionProve that:sin−1(817)+sin−1(35)=tan−1(7736)
View SolutionProve that sin−1(513)+sin−1(1665)=cos−1(45)
View SolutionProve that sin−1(817)+sin−1(35)=cos−1(3685)
View SolutionProve that:cos−1(1213)+sin−1(35)=sin−1(5665)
View SolutionShow that : sin−1(35)+sin−1(817)=cos−1(3685).
View SolutionProve that
sin−1.817+cos−1.45=cos−1.3685View SolutionProve that sin−1(35)+cos−1(1517)=cos−1(3685)
View SolutionProve that :2sin−1(35)=tan−1(247)
View SolutionProve that: sin−1(45)+sin−1(513)+sin−1(1665)=π2
View Solution

