If cos−1x>sin−1x, then
A
1√2<x≤1
B
0≤x≤1√2
C
−1≤x<1√2
D
x>0
Video Solution
Text Solution
The correct Answer is:C
We have, cos1x>sin−1x, where x∈[−1,1]
⇒x<cos(sin−1x)
⇒x<cos[cos−1√1−x2],[letsin−1x=θ⇒sinθ=x1] v
[∵cosθ=√1−sin2θ=√1−x2⇒cos−1√1−x2]
⇒x<√1−x2
⇒x2<1−x2⇒2x2<1
⇒x2<12⇒x±(1√2).....(i)
Also, −1≤x≤1.....(ii)
∴−1≤x≤1√2
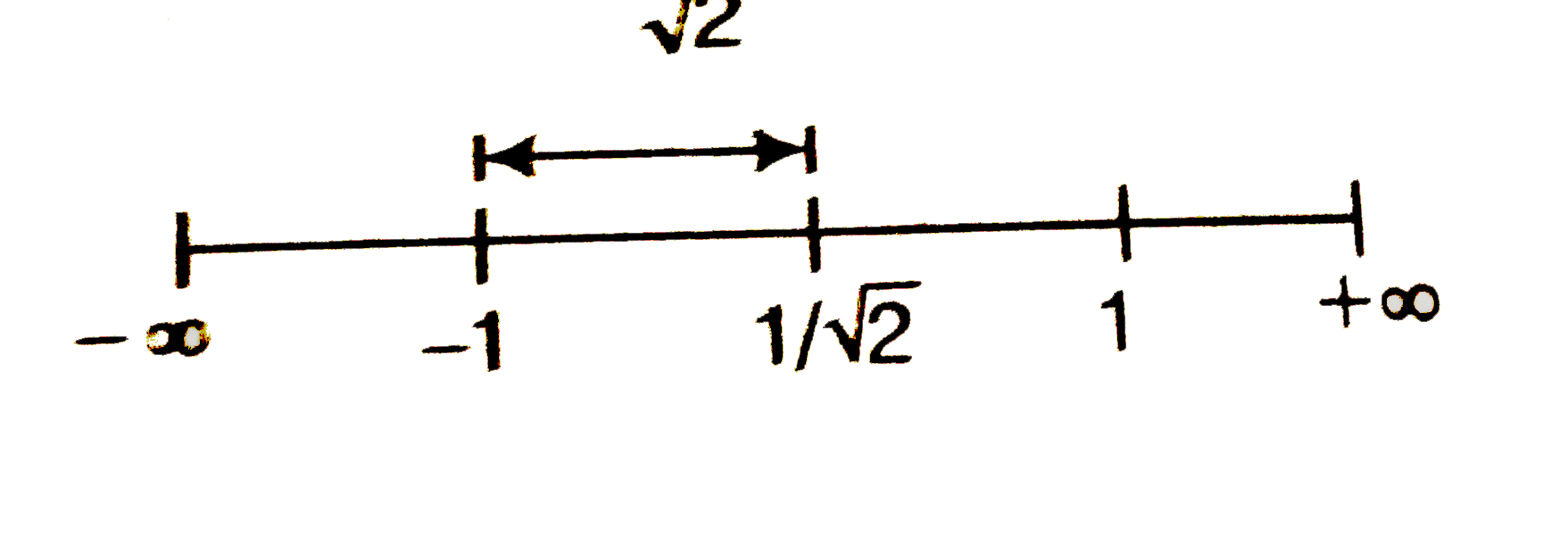
Alternate Method
π2−sin−1x>sin−1x
π2>2sin−1x⇒π4>sin−1x
1√2>x⇒1√2<x≤1
We know that, sin−1x∈[−π2,π2]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If cos−1x=tan−1x, then sin(cos−1x)=
AxBx2C1/xD1/x2If cos−1x=tan−1x, then sin(cos−1x)=
AxBx2C1/xD1/x2sin−1x>cos−1x holds for
Aall values of xBx∈(0,1/√2)Cx∈(1/√2,1)Dx=1.75
∫sin−1x−cos−1xsin−1x+cos−1xdx=
View SolutionSTATEMENT -1 : If [sin−1x]>[cos−1x],where [] represents the greatest integer function, then x∈[sin1,1] is
and
STATEMENT -2 : cos−1(cosx)=x,x∈[−1,1]
View SolutionLet x∈(0,1). The set of all x such that sin−1x>cos−1x is the interval
View SolutionIf cos−1(cos4)>3x2−4x then
View SolutionLet a=(sin−1x)sin−1x,b=(sin−1x)cos−1x,c=(cos−1x)sin−1x, d and if =(cos−1x)cos−1xx∈(0,1) then
View Solution
