(Cosine Formulae) if $a, b, c$ are the lengths of the sides opposite respectively to the angles $A, B, C$ of a triangle $A B C,$ show that $cos A \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ (ii) $cos B \frac{c^{2} + a^{2} - b^{2}}{2 a c}$ (iii) (i) $cos C \frac{a^{2} + b^{2} - c^{2}}{2 a b}$

Video Solution

Text Solution

Verified by Experts

Here, components of C are c cos A and c sin A is drawn.

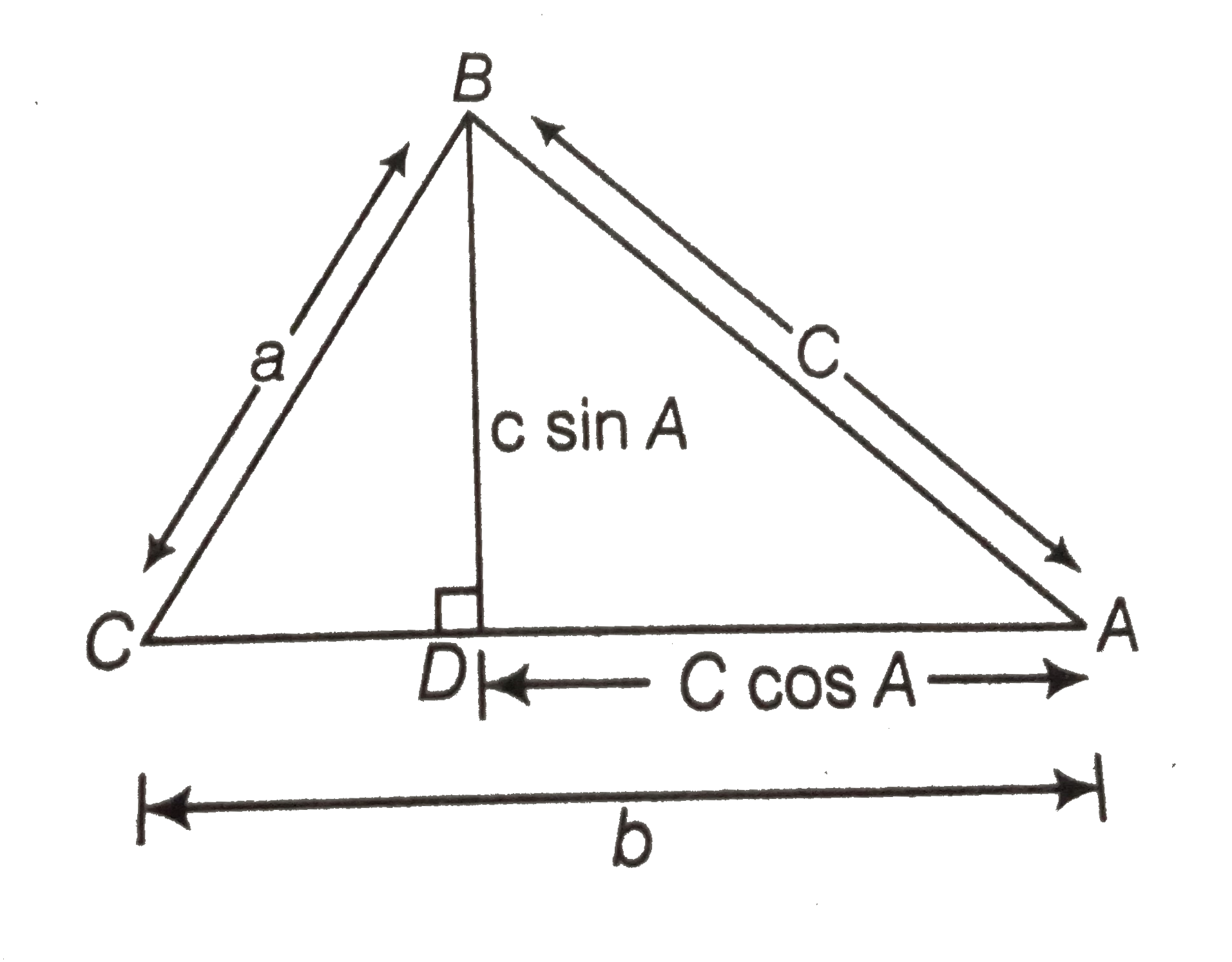
Since, $- - \to C D = b - c cos A$
In $Δ B D S a^{2} = {(b - cos A)}^{2} + {(c sin A)}^{2}$
$\Rightarrow a^{2} = b^{2} + c^{2} {cos}^{2} A - 2 b c cos A + c^{2} {sin}^{2} A$
$\Rightarrow 2 b c cos A = b^{2} - a^{2} + c^{2} ({cos}^{2} A {sin}^{2} A)$
$∴ cos A = \frac{b^{2} + c^{2} - a^{2}}{2 a b}$

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

BOOK - NCERT EXEMPLARCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Three Dimensional Geometry
46videos
THREE DIMENSIONAL GEOMETRY

Similar Questions

Knowledge Check

Question 1 - Select One or More
In a $△ A B C$ , acosB + b cosC + c cosA $= \frac{a + b + c}{2}$ then
ATriangle in isosceles
BTriangle may be equilateral
C $sin (A - B) + sin (B - C) + sin (C - A) = \frac{3}{2}$
D $4 sin (\frac{A - B}{2}) sin (\frac{B - C}{2}) sin (\frac{C - A}{2}) = 1$
Question 2 - Select One
In $△ A B C, a (b^{2} + c^{2}) cos A + b (c^{2} + a^{2}) cos B + c (a^{2} + b^{2}) cos C =$
A $0$
B $3 a b c$
C $3 a^{2} b c$
D $3 a b^{2} c$
Question 3 - Select One
If the angles A,B,C of a triangle are in A.P. and sides a,b,c, are in G.P., then prove that $a^{2}, b^{2}, c^{2}$ are in A.P.
AA.P.
BH.P.
CG.P.
Dnone of these

NCERT EXEMPLAR-VECTOR ALGEBRA-Vector Algebra

Home
Ask Doubt
Profile