If $\to a, \to b and \to c$ determine the vertices of a triangle, show that $\frac{1}{2} [\to b \times \to c + \to c \times \to a + \to a \times \to d]$ givens the vector area of the triangle. Hence, deduce the condition that the three points $\to a, \to b and \to c$ are collinera. Also, find the unit vector normal to the plane of the triangle.

Video Solution

Text Solution

Verified by Experts

Since, $\to a, \to b and \to c$ are the vertices of a $Δ A B C$ as shown.

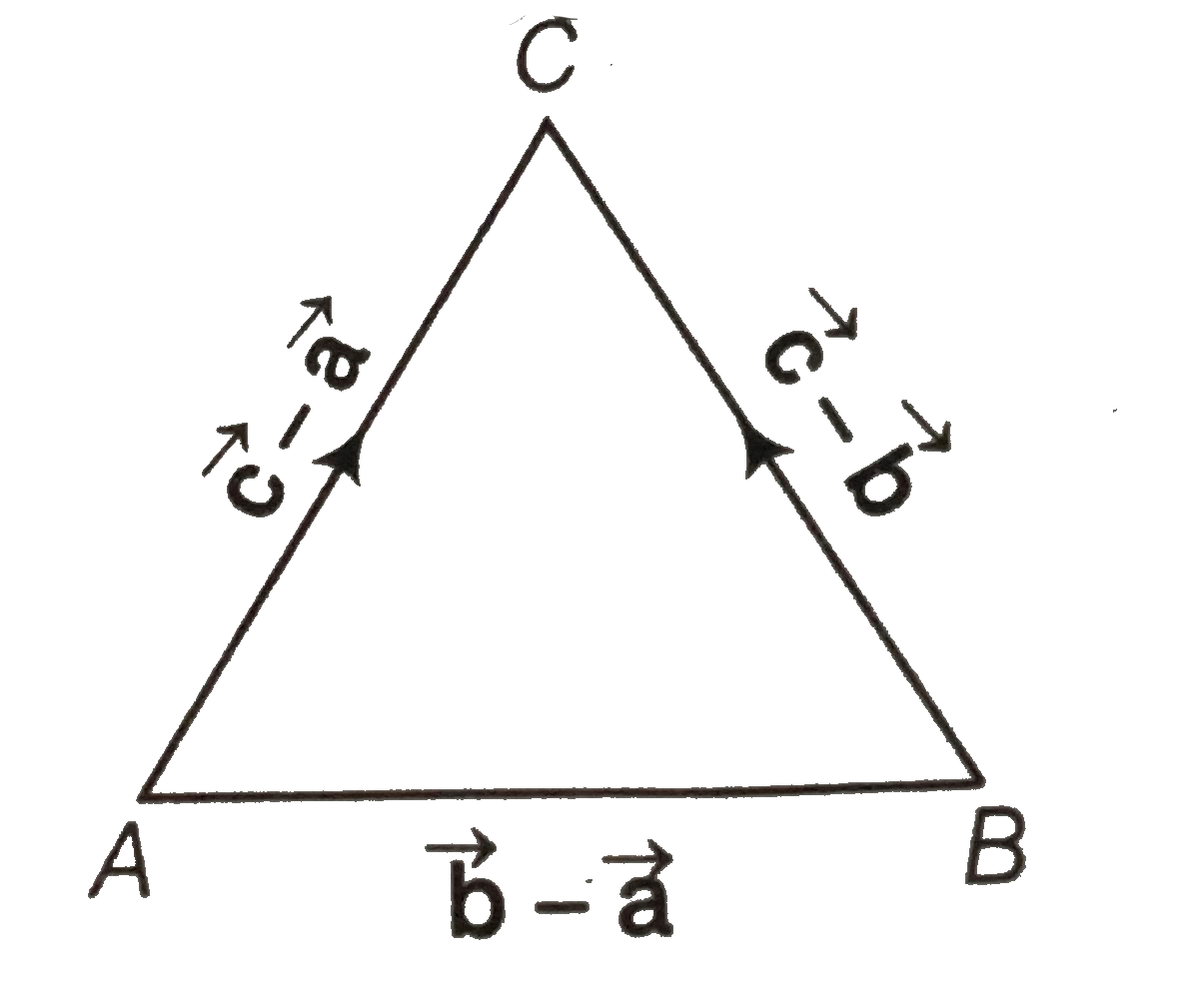
:. Area of $Δ A B C = \frac{1}{2} ∣ ∣ ∣ - - \to A B \times - - \to A C ∣ ∣ ∣$
Now, $- - \to A B = \to b - \to a and - - \to A C = \to c - \to a$
:.Area of $Δ A B C = \frac{1}{2} ∣ ∣ \to b - \to a \times \to c - \to a ∣ ∣$
$= \frac{1}{2} ∣ ∣ \to b \times \to c - \to b \times \to a - \to a \times \to c + \to a \times \to a ∣ ∣$
$= \frac{1}{2} ∣ ∣ \to b \times \to c + \to a \times \to b + \to c \times \to a + \to 0 ∣ ∣$
$= \frac{1}{2} ∣ ∣ \to b \times \to c + \to a \times \to b + \to c \times \to a ∣ ∣ ... ... . (i)$
For three points to be collinear, area of the $Δ A B C$ should be equal to zero.
$\Rightarrow \frac{1}{2} [\to b \times \to c + \to c \times \to a + \to a \times \to b] = 0$
$\Rightarrow \to b \times \to c + \to c \times \to a + \to a \times \to b = 0 ... ... . (i i)$ This is the requried conddition for collinearity of three points $\to a, \to b and \to c$ .
Let $ˆ n$ be the unit normal to the plane of the $Δ A B C$ .
$∴ ˆ n = \frac{- - \to A B \times - - \to A C}{∣ ∣ ∣ - - \to A B \times - - \to A C ∣ ∣ ∣}$
$= \frac{\to a \times \to b + \to b \times \to c + \to c \times \to a}{∣ ∣ \to a \times \to b + \to b \times \to c + \to c \times \to a ∣ ∣}$

Updated on:21/07/2023

The vector area of triangle whose sides are $\to a, \to b, \to c$ is
A $\frac{1}{2} ∣ ∣ \to b \times \to c + \to c \times \to a + \to a \times \to b ∣ ∣$
B $\frac{1}{2} ∣ ∣ \to b \times \to c + \to c \times \to a + \to b ∣ ∣$
C $\frac{1}{3} ∣ ∣ \to b \times \to c + \to c \times \to a + \to b ∣ ∣$
D $\frac{1}{2} ∣ ∣ - \to b \times \to c + \to c \times \to a + \to b ∣ ∣$
In a righht angled triangle the three vectors $\to a, \to b$ and $\to c$ add to zero. Then $\to a, \to b$ is

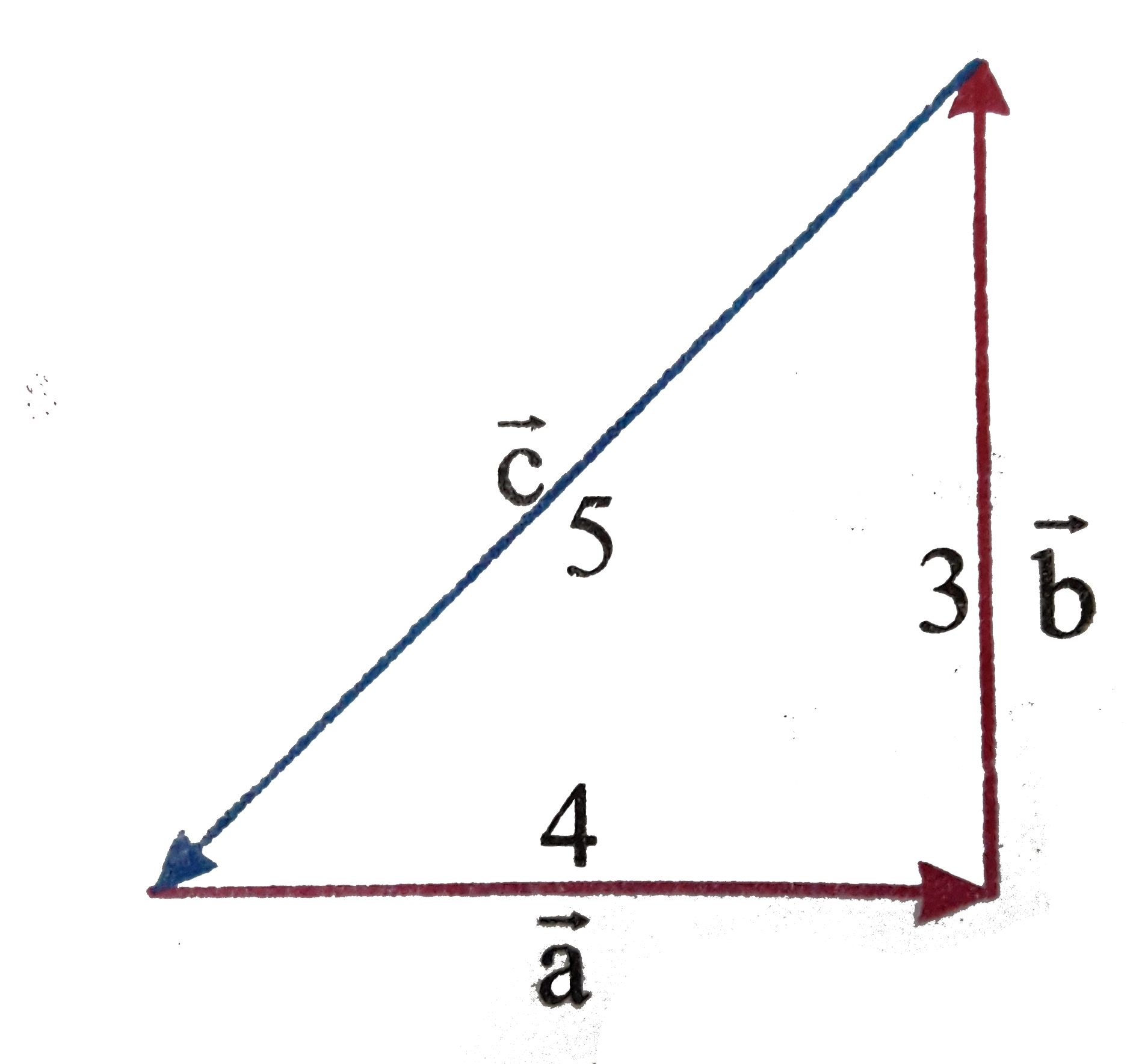A $- 9$
B $+ 9$
C0
D $- 3$
If $\to a, \to b, \to c$ are the position vectors of the vertices. A,B,C of a triangle ABC. Then the area of triangle ABC is
A $\frac{1}{2} ∣ ∣ \to a \times \to b + \to b \times \to c + \to c \times \to a ∣ ∣$
B $\frac{1}{2} ∣ ∣ \to a \times \to b ∣ ∣$
C $\frac{1}{2} ∣ ∣ \to b \times \to c ∣ ∣$
D $\frac{1}{2} | \to c \times \to a |$