A company makes 3 model of calculators, A, B and C at factory I and factory II. The company has orders for atleast 6400 calculators of model A, 4000 calculators of model 8 and 4800 calculators of model C. At factory I, 50 calculators of model A, 50 of model 8 and 30 of model C are made everyday, at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs ? 12000 and 1 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
The correct Answer is:N/a
Let the factory I operate for x days and the factory II operate for y days. At factory l, 50 calculators of model A and at factory II, 40 calculators of model A are made everyday. Also, company has ordered for atleast 6400 calculators of model A.
Also, at factory l, 50 calculators of model 8 and at factory II, 20 calculators of modal 8 are made everyday Since, the company has ordered atleast 4000 calculators of model B
Similarly for model C, 30x+40y ge 4800
Also,
If costs 12000 and 15000 each day to operate factories I and II respectively.
Corresponding LPP is
Minimise Z=12000x+15000y, "subject to"
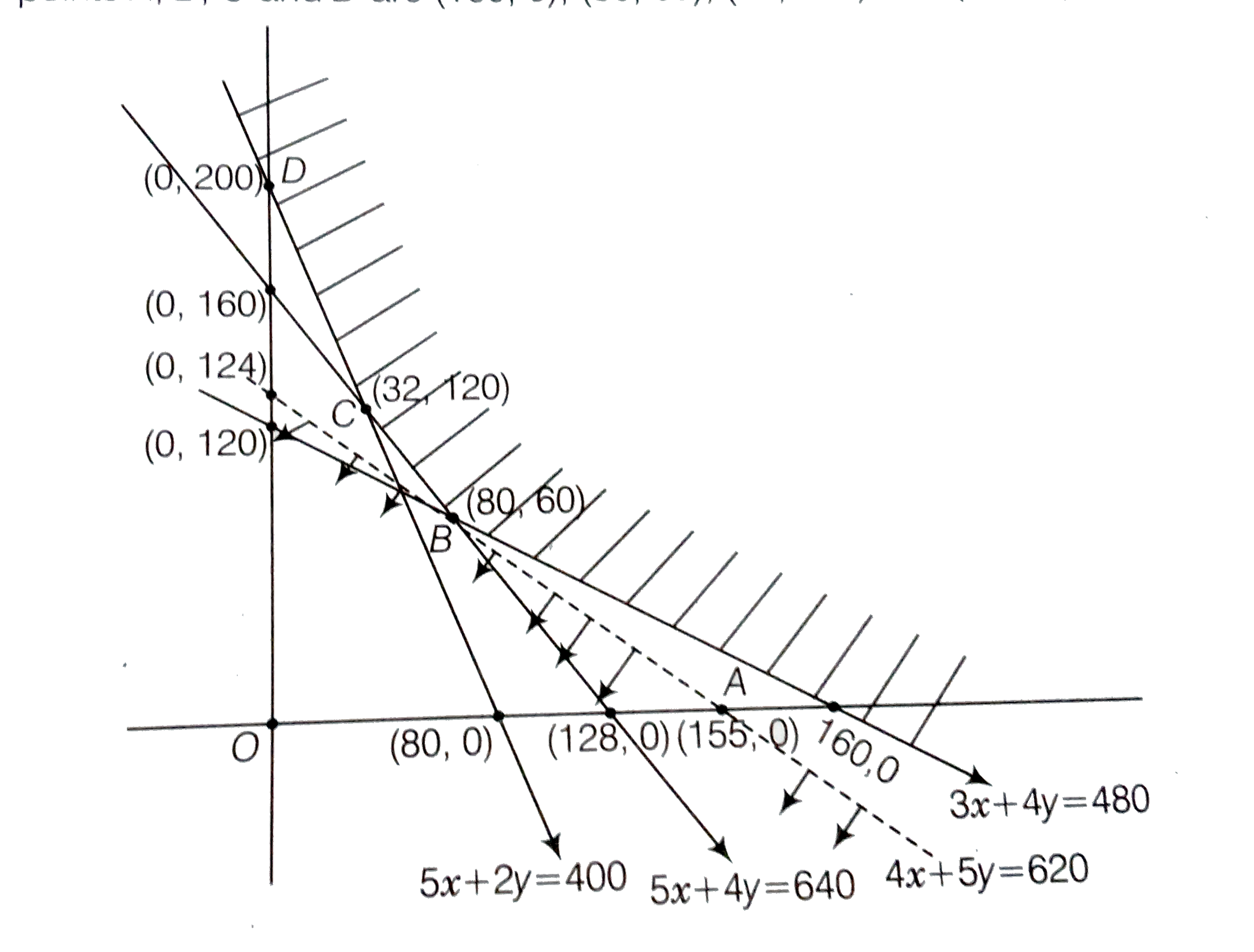
on solving 3x+4y=480 and 5x+4y=640, we get x=80, y=60
On solving 5x+4y=640, we get x =32, y=120
Thus from the graph it is clear that feasible region is unbounded and the coordinates of corner points A,B,C and D are (160,0),(80,60),(32,120) and (0,200) respectively
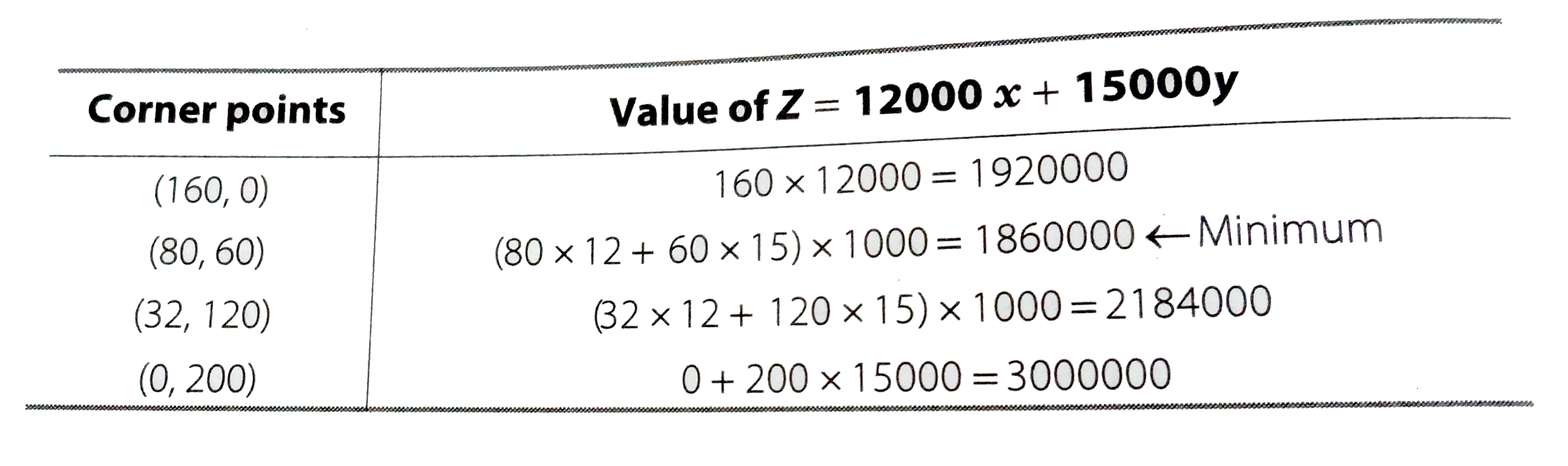
From the above table, it is clear that for given unbouded region the minimum valur of Z may or may not be 1860000.
Now for deciding this, we graph, the inequality
12000x+15000y lt 1860000
and check whether the resulting open half plane has points in common with feasible region or not. Thus, as shown in the figure it has no common points so, Z=12000x+15000y has minimum value 1860000. Som number of day factory I should be operated is 80 and number of days factory II should be operated is 60 for the minimum cost and satisfying the given constraints.
Topper's Solved these Questions
Similar Questions
A company manufactures three kinds ofcalculators: A,BandC in its two factoriesI and II. The company has got an order form anufacturing at least 6400 calculators of kind A, 4000 of kind B and 4800 of kind C.The daily output of factory I is of 50 calculators of kind A, 50 calculators of kind Band 30 calculators of kind C. The daily out put of factory II is of40 calculators of kind A, 20 of kind B and 40 of kind C. The cost per day to run factory I is 12000 and of factory II is15000. How many days do the two factories have to be in operation to produce the order with the minimum cost? Formulate this problem as an LPP and solve it graphically.
View SolutionAtomic model | Bohrs Model
View Solutionthomson model || Rutherford model
View SolutionWhy is Rutherford model called a nuclear model ?
View SolutionWhy is Rutherford.s model called planetary model?
View SolutionRutherford's atomic model is called the 'planetary model of an atom'.
View SolutionA model of an aeroplane is made to a scale of 1 : 400. Calculate :
the length, in m, of the aeroplane, if length of its model is 16 cm.
View SolutionA model of an aeroplane is made to a scale of 1 : 400. Calculate :
the length, in cm, of the model, if the length of the aeroplane is 40 m.
View Solutionmodels of Atom(Thomson model)
View SolutionIf Thomson model is considered to be true then in Rutherford model
View Solution
