The optical properties of a medium are governed by the relative permittivity (εr) and relative permeability (μr). The refractive index is defined as √μrεr=n. For ordinary material, εr>0 and μr>0 and the positive sign is taken for the squre root.
In 1964, a Russian scientist V. Veselago postualted the existance of material with εr<0 and μr<0 . Since, then such metamaterial have been produced in the laboratories and their optical properties studied. For such materials n=−√μrεr. As light enters a medium of such refractive index the phases travel away from the direction of propagation.
(i) According to the description above show that if rays of light enter such a medium from air ( refractive index =1) at an angle theta in 2nd quadrant, then the refracted beam is in the 3rd quadrant.
(ii) Prove that Snell's law holds for such a medium.
Let us assume that the given postulate is true, then two parallel ray would proceed as shown in the figure below.
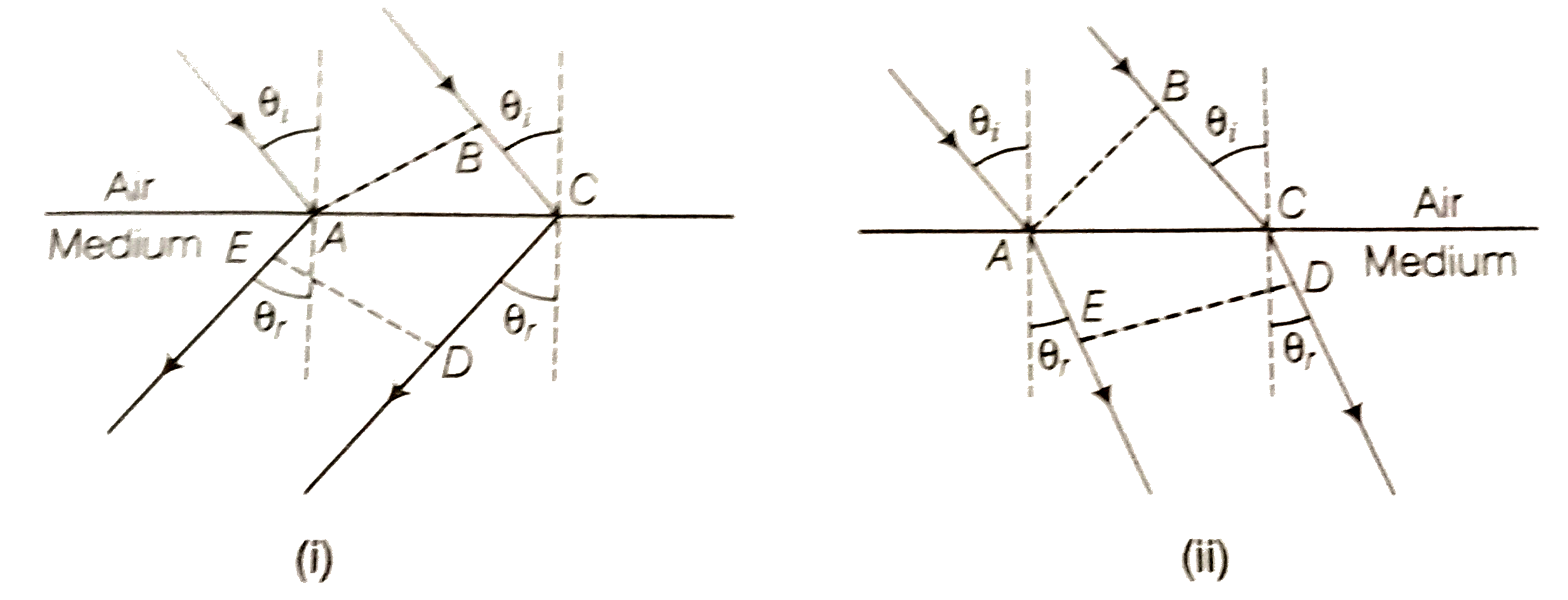
(i) Let AB represent the incident wavefront and DE represent the refracted wavefront. All points on a wavelength must be in same phase and in turn, must have the same optical path length.
Thus, −√εrμrAE=BC−√εrμrCD
BC=√εrμr(CD−AE)
BC>0,CD>AE
As showing that the postualte is reasonable. If however, the light proceeded in the same it does for ordinary material ( viz. in the fourth quadrat , Fig. 2)
Then, −√εrμrAE=BC−√εrμrCD
BC=√εrμr(CD−AE)
If BC>0, then CD>AE
which is obvious from Fig. (i).
Hence, the postulate reasonable.
However, if the light proceeded in the sense it does for ordinary material, ( going from 2nd quadrant to 4 the quadrant ) as shown in Fig. (i)., then proceeding as above,
−√εrμrAE=BC−√εrμrCD
or BC=√εrμr(CD−AE)
As AE>CD, therefore BC<0 which is not possible. Hence, the given postulate is correct.
(ii) From Fig. (i)
BC=ACsinθi
and CD−AE=ACsinθr
As BC=√μrεr [CD−AE=BC]
∴ACsinθi=√εrμrACsinθr
or sinθisinθr=√εrμr=n
Which proves Snell's law.
Topper's Solved these Questions
Similar Questions
The optical properties of a medium are governed by the relative permitivity (εr) and relative permeability (μr). The refractive index is defined as √μrεr=n. For ordinary material εr>0 and μr>0 and the positive sign is taken for the square root. In 1964, a Russian scientist V. Veselago postulated the existence of material with εr<0andμr<0. Since then such 'metamaterials' have been produced in the laboratories and their optical properties studied. For such materials n=−√μrεr. As light enters a medium of such refractive index the phases travel away from the direction of propagation.
(i) According to the description above show that if rays of light enter such a medium from air (refractive index = 1) at an angle θ in 2nd quadrant, then the refracted beam is in the 3rd quadrant.
(ii) Prove that Snell's law holds for such a medium.
View SolutionWrite the formula for the velocity of light in
a material medium of relative permitivity ∈r and relative magnetic permeability μr.
View Solution
Knowledge Check
The optical properties of a medium are governed by the relative permitivity (εr) and relative permeability (μr). The refractive index is defined as √μ1εr=n . For ordinary sing is taken for the square root. In 1964, a Russian scientist V. Veselago postulated the existence of material with εr<0 and μr<0 . Since then such 'meta materials' have been produced in the laboratorised and their optical properties studied. For such materials n=−√μrεr. As light entes a medium of such refractive index the phases traval away front the direction ofpropagation.
For light incident from air on the meta materials, then appropriate ray diagram isA B
B C
C D
D
The optical properties of a medium are governed by the relative permitivity (εr) and relative permeability (μr). The refractive index is defined as √μ1εr=n . For ordinary sing is taken for the square root. In 1964, a Russian scientist V. Veselago postulated the existence of material with εr<0 and μr<0 . Since then such 'meta materials' have been produced in the laboratorised and their optical properties studied. For such materials n=−√μrεr. As light entes a medium of such refractive index the phases traval away front the direction ofpropagation.
Consider following statements
i) Snall's slaw valid for these mater ials
ii) Snell's slaw is not valid for these mater ials
iii) Speed of light in these mater ial is v=c|n|
iv) Speed of light in these material is v=cAI, iii are correctBI, iv are correctCii, iv are correctDii, iii are correctThe relative permeability (μr) of a substance is related to its susceptibility (χ) as
Aμr=I−χBμr=I+χCμr=I−χ2Dμr=I+χ2
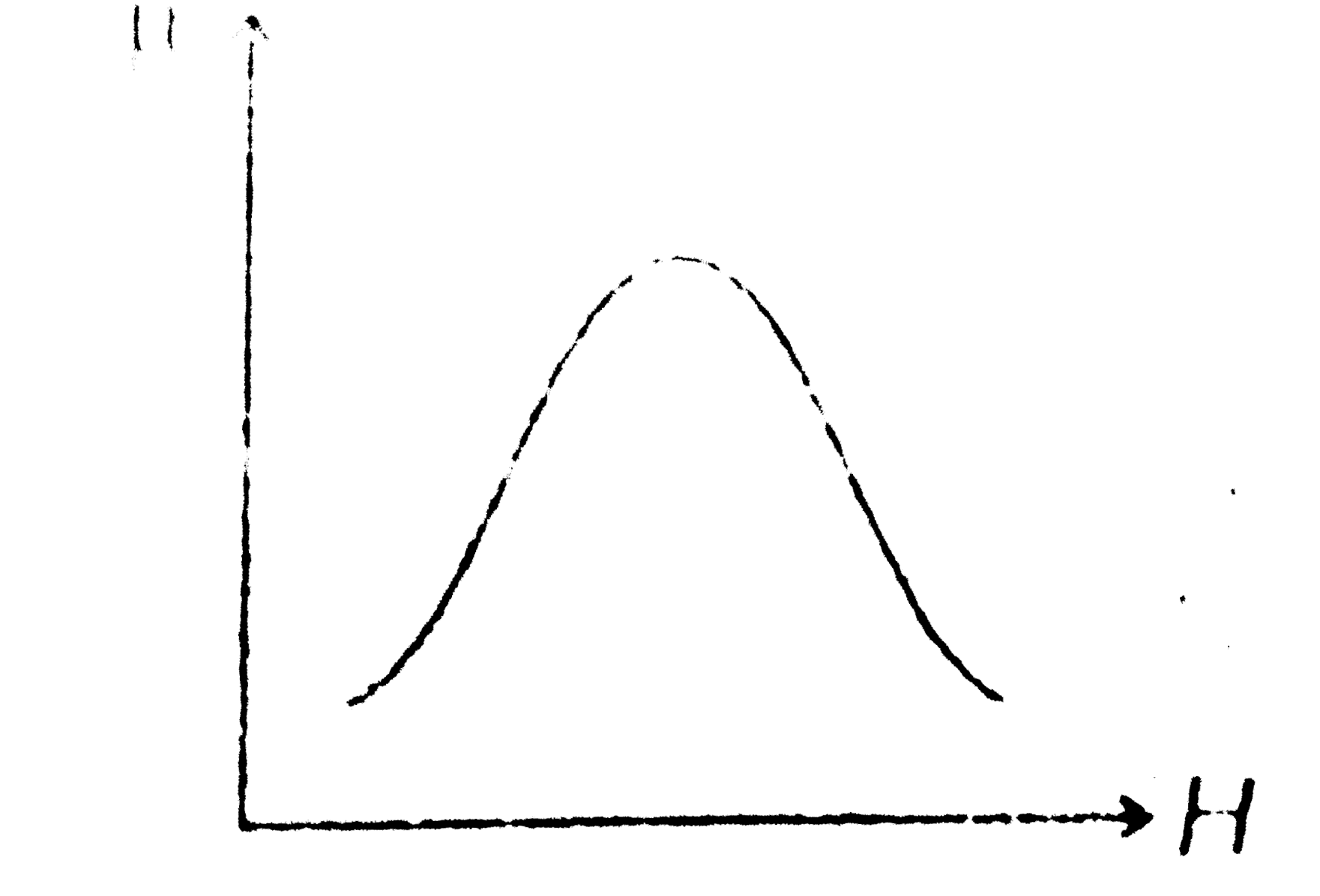
Variation of μr (relative permeability) with magnetizing field as shown in figure is for
View SolutionThe relative permeability (μr) of a ferromagnetic substance varies with tamperature (T) according to the curve

View SolutionThe dimensional formula μ0ε0 is
View SolutionWhich of the following is not correct about relative magnetic permeability (μr)?
View SolutionFor ferromagnetic material, the relative permeability (mu_(r)), versus magnetic intensity (H) has the following shape
View Solution
