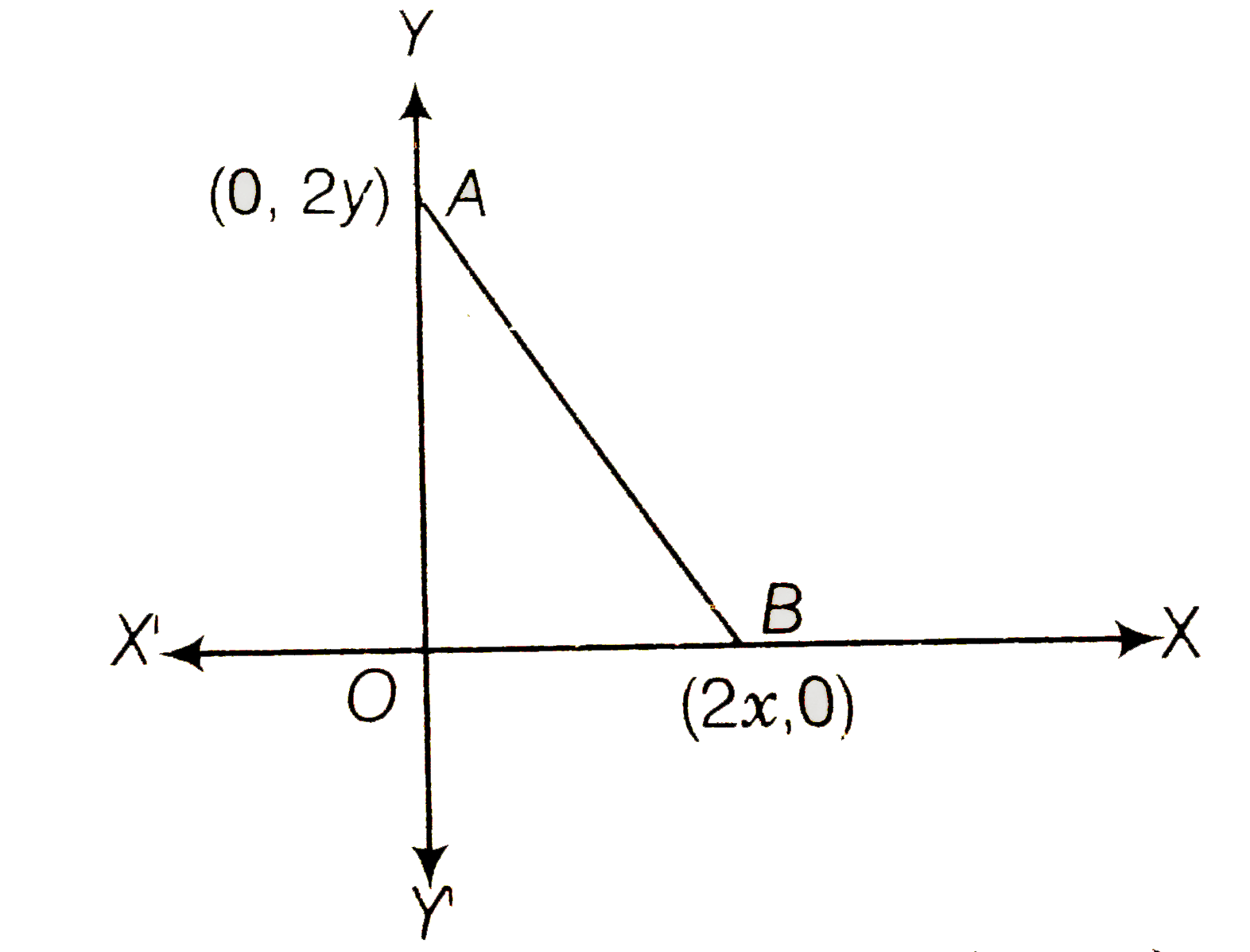
The coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
The coordinates of the point which is equidistant from the three vertices of the triangle AOB as shown in the figure is

A

(x,y)

B

(y,x)

C

(x2,y2)

D

(y2,x2)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Let the coordinate of the point which is equidistant from the three vertices O(0,0),A(0,2y) and B(2x,0) is P(h,k).
Then, PO=PA =PB
⇒(PO)2=(PA)2=(PB)2 ...(i)
By distance formula,
[√(h−02)+(k−0)2]2=[√(h−02)+(k−2y)2]2=[√(h−2x)2+(k−0)2]2
⇒h2+k2=h2+(k−2y)2=(h−2x)2+k2 ...(ii)
Taking first two equations , we get
h2+k2=h2+(k−2y)2
⇒k2=k2+4y2−4yk⇒4y(y−k)=0
[∴y≠0]
⇒y=k
Taking first and equations , we get
h2+k2=(h−2x)2+k2
⇒h2=h2+4x2−4xh
⇒4x(x−h)=0
⇒x=h [∴x≠0]
∴ Required points =(h,k)=(x,y)

Updated on:21/07/2023
|
Class 10MATHSCOORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The coordinates of the point which is equidistant from "the three vertices of the △AOB is:
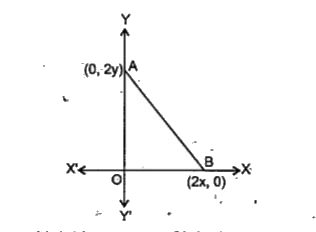    ocr_image

    A(x,y)
    B(y,x)
    C(x2,y2)
    D(y2,x2)

  • The loucs of the point which is equidistant from the three determined by the sides of a triangles is _______

    Athe in-centre
    Bthe ex-centre
    Cthe ortho-centre
    Deither (a) or (b)

  • The equidistant point from the vertices of a triangle is called its :

    ACentroid
    BIncentre
    CCircumcentre
    DOrthocentre