In the formula ¯x=a+∑fidi∑fi
for finding the mean of grouped data di'S and deviation from a of
lower limits of the classes
upper limits of the classes
mid-points of the classes
frequencies of the class marks
The correct Answer is:C
We know that, di=xi−a
i.e., di's are the deviation from a of mid-points of the classes
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLARCHAPTER - STATISTICS AND PROBABILITYEXERCISE - VERY SHORT ANSWERS QUESTIONS
2 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLARCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS
5 Videos
- REAL NUMBERSBOOK - NCERT EXEMPLARCHAPTER - REAL NUMBERSEXERCISE - Real Numbers
39 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLARCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Surface Areas And Volumes
62 Videos
Similar Questions
Knowledge Check
Choose the correct answer from the given four options:
In the formula x=a+∑x1di∑fi for finding the mean of grouped data di 's are the deviations from a ofAlower limits of the classesBupper limits of the classesCmid-points of the classesDfrequencies of the class marksIn the formula ¯x=a+h∑fiui∑fi
for finding the mean of grouped frequency distribution ui is equal toAxi+ahBh(xi−a)Cxi−ahDa−xihIf ∑fiui=36, ∑fi=100, A=40 and h=3, then ¯¯¯X=?
A41.08B38.92C39.64D40.36
In Calculating the mean of grouped data, grouped in classes of equal width, we may use the formula
¯x=a+∑fidi∑fi
Where, a is the assumed mean, a must be one of the mid point of the classes. Is the last statement correct? Justify your answer.
View SolutionFind ¯uif∑fiui=66and∑fi=100.
View SolutionThe algebraic sum of the deviations of xifi from the mean is:
View SolutionThe measurments ( in mm) of the diameters of the head of the screws are given below :
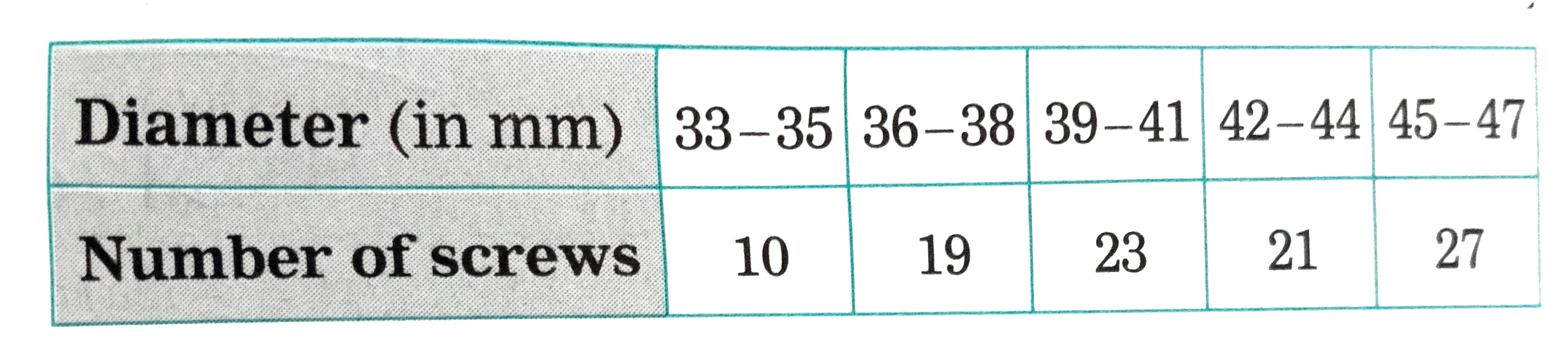
Calculate the mean diameter of the screw by ' Assumed Mean Method' .
Steps to calculate mean by this method :
(1) Assume mean A. In this example , A = 40. (Generally, the class mark of the class having the maximum frequency or the class mark of the middle class is chosen as the assumed mean.)
(2) In column 1, write the class intervals,(Here, diameter).
(3) In column 2, write the corresponding class marks.
(4) In column 3, write the value of di, where di=xi−A.
A is the assumed mean.
(5) In column 4, write the frequencies (fi). Write Σfi at the bottom of this column.
(6) In column 5, write the product (fi×di) and their sum Σfidi.
Calculate ¯d and ¯¯¯X using the following formulae :
¯d=ΣfidiΣfi. Mean¯¯¯X=A+¯d.
[d : mean of deviations.]
View SolutionIf for distribution of 18 observations ∑(xi−5)=3and∑(xi−5)2=43, find the mean and standard deviation.
View Solution
