Draw a $Δ$ ABC. Take a point D on BC. Join AD How many triangles do you get? Name them.

Video Solution

Text Solution

Verified by Experts

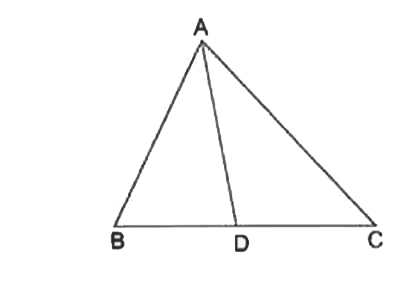
The correct Answer is:Three , $Δ A B D, Δ A D C$ and $Δ A B C$

Answer

Step by step video, text & image solution for Draw a Delta ABC. Take a point D on BC. Join AD How many triangles do you get? Name them. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.

Updated on:21/07/2023

Class 6 MATHS BASIC GEOMETRICAL IDEAS

Topper's Solved these Questions

BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 16B (objective questions)
11videos
TRIANGLES
BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 16B (objective questions)
11videos
TRIANGLES
BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL SHAPESEXERCISE - EXERCISE
8videos
THREE-DIMENSIONAL SHAPES
BOOK - RS AGGARWALCHAPTER - TWO-DIMENSIONAL REFLECTION SYMMETRY (LINEAR SYMMETRY)EXERCISE - EXERCISE
10videos
TWO-DIMENSIONAL REFLECTION SYMMETRY (LINEAR SYMMETRY)

Knowledge Check

Question 1 - Select One
In a $Δ A B C, D$ is a point on BC. AB is the hypotenus of then which relation is correct .
A $A B^{2} + C D^{2} = B C^{2} + A D^{2}$
B $C D^{2} + B D^{2} = 2 A D^{2}$
C $A B^{2} + A C^{2} = 2 A D^{2}$
D $A B^{2} + A D^{2} = B D^{2}$

In $Δ A B C, A D = B C$ . Find x.
View Solution
Write answers to the following questions :
ABCDEF is a hexagon. How many triangles will you get, if you join point A to the remaining points ?
View Solution
In $Δ A B C, D$ is the mid-point of BC . Length AD is 27 cm . N is a point in AD such that the length of DN is 12 cm . The distance of N from the centroid of $Δ A B C$ is equal to
View Solution
In a $Δ A B C$ , if D is the mid point of BC and AD is perpendicular to AC, then $cos B =$
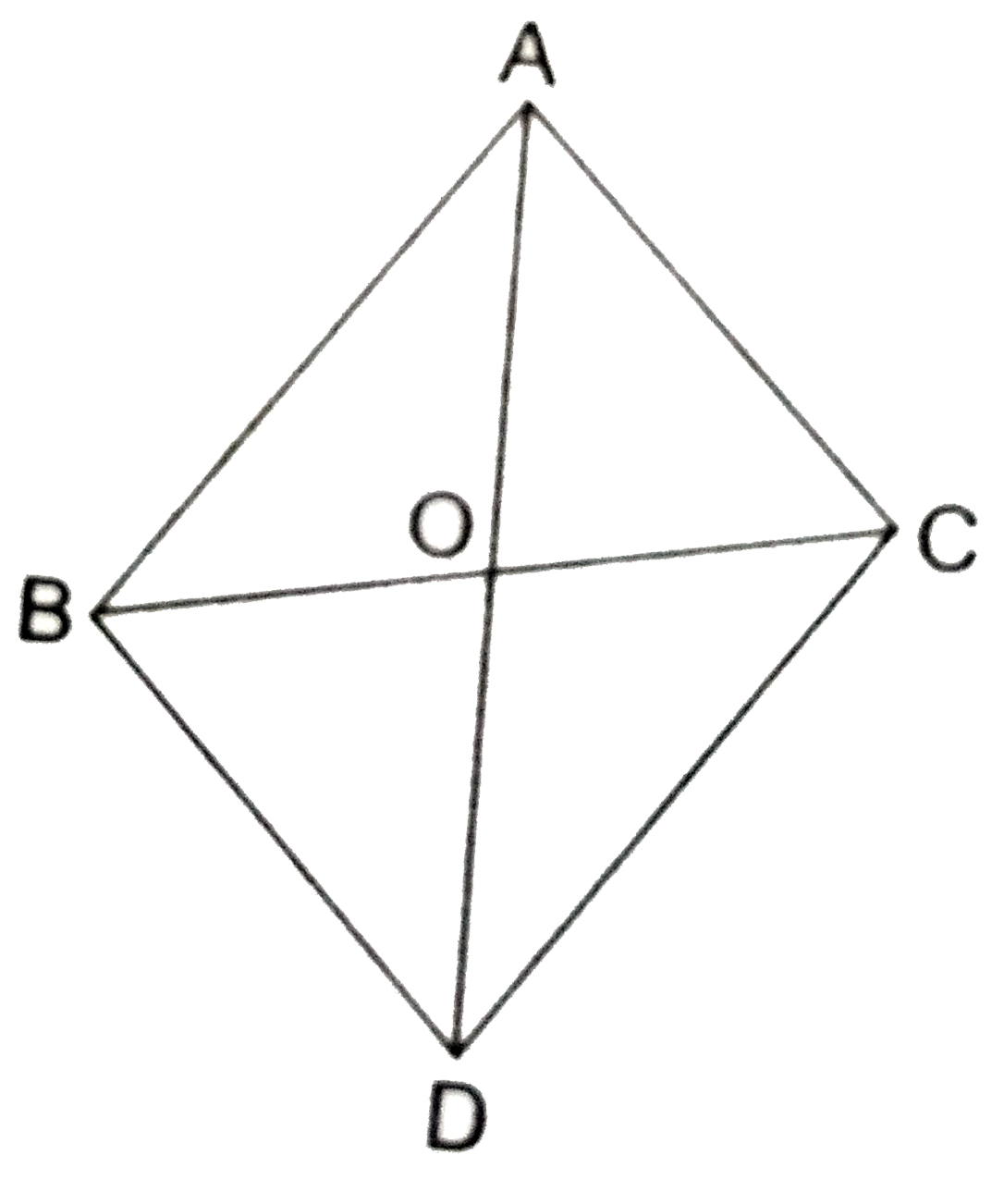
View Solution
In the same figure, $Δ A B C and Δ D B C$ are on the same base BC . If AD is intersects BC at O, prove that
$\frac{a r (Δ A B C)}{a r (Δ D B C)} = \frac{A O}{D O}$

View Solution
In a $Δ A B C, A B = A C = 17 c m D$ is a point on BC such that $A D = 15, C D = 4 c m$ , find BD=?
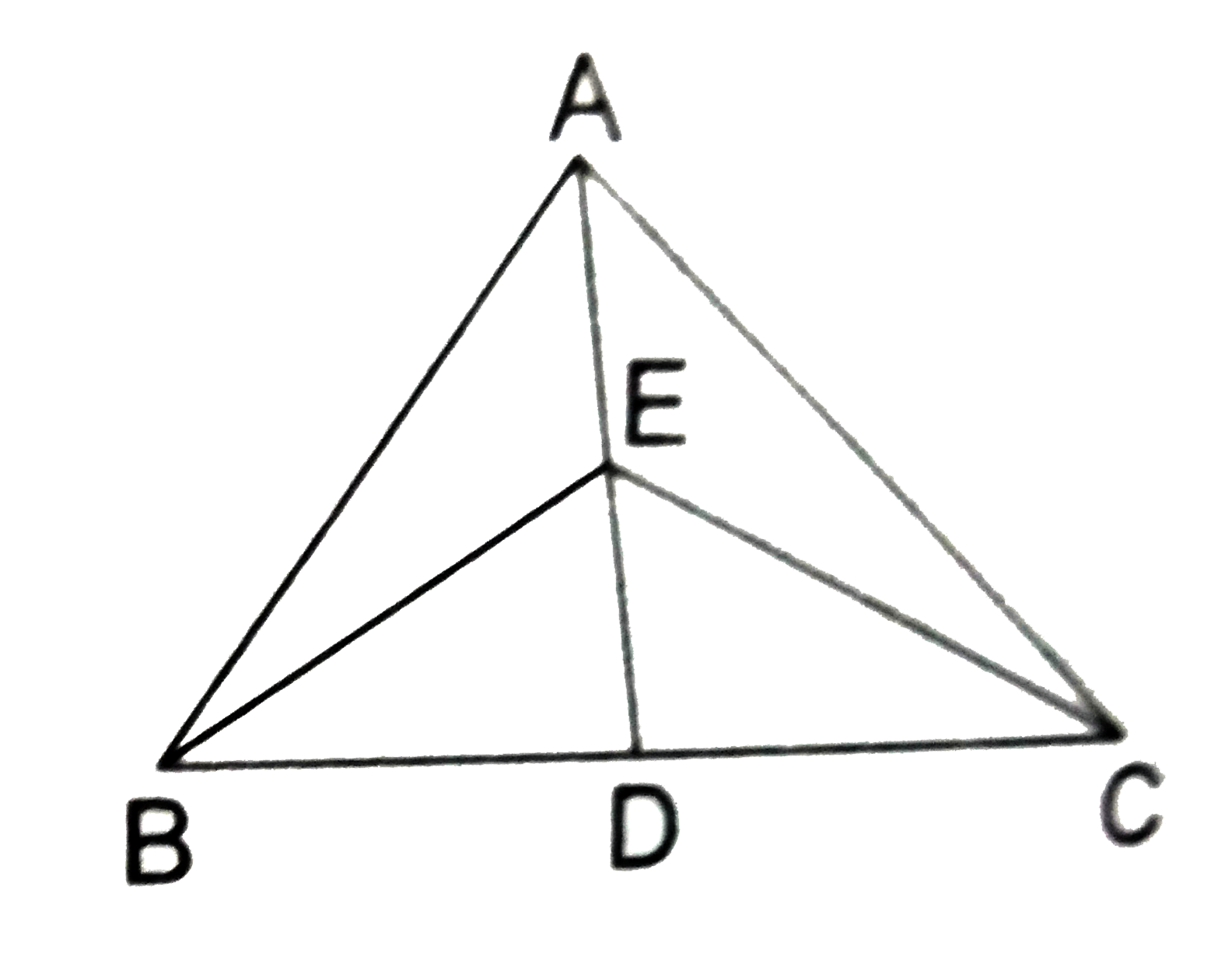
View Solution
The vertex A of $△ A B C$ is joined to a point D on the side BC. The midpoint of AD is E.
Prove that $a r (△ B E C) = \frac{1}{2} a r (△ A B C)$ .

View Solution

RS AGGARWAL-TRIANGLES-EXERCISE 16A

Take three noncollinear points A, B and C on a page of your notebook. ...
02:26
The measures of two angles of a triangle are 72^(@) and 58^(@). Find t...
01:39
The angles of a triangle are in the ratio 1:3:5. Find the measure of e...
02:34
One of the acute angles of a right triangle is 50^(@). Find the other ...
01:36
One of the angles of a triangle is 110^(@) and the other two angles ar...
04:13
If one angle of a triangle is equal to the sum of other two, show that...
03:50
In a A B C ,\ if\ 3/\ \ A=4/\ B=6/\ C , calculate the angles.
03:20
Look at the figure given below. State triangle whether it is acute, ri...
03:58
In the given figure. State triangle whether it is scalene, isosceles o...
06:23
Draw a Delta ABC. Take a point D on BC. Join AD How many triangles do ...
03:06
Can a triangle have: Two right angles? (ii) Two obtuse angles? Two acu...
03:06
A triangle has ...... sides, ...... angles and ...... vertices.
01:48
The sum of the angles of a triangle is .......
01:06
The sides of a scalene triangle are of ........... lengths.
01:21
Each angle of an equilateral triangle measures .......
02:24
The angles opposite to equal sides of an isosceles triangle are .........
01:34
The sum of the lengths of the sides of a triangle is called its .........
01:17

Home
Ask Doubt
Profile

Draw a Δ ABC. Take a point D on BC. Join AD How many triangles do you get? Name them.

The correct Answer is:Three ,ΔABD,ΔADC and ΔABC

Topper's Solved these Questions

Similar Questions

Knowledge Check

In a ΔABC,D is a point on BC. AB is the hypotenus of then which relation is correct .

RS AGGARWAL-TRIANGLES-EXERCISE 16A

Draw a $Δ$ ABC. Take a point D on BC. Join AD How many triangles do you get? Name them.

The correct Answer is:Three , $Δ A B D, Δ A D C$ and $Δ A B C$

In a $Δ A B C, D$ is a point on BC. AB is the hypotenus of then which relation is correct .