The vertex A of is joined to a point D on the side BC. The midpoint of AD is E.
Prove that .
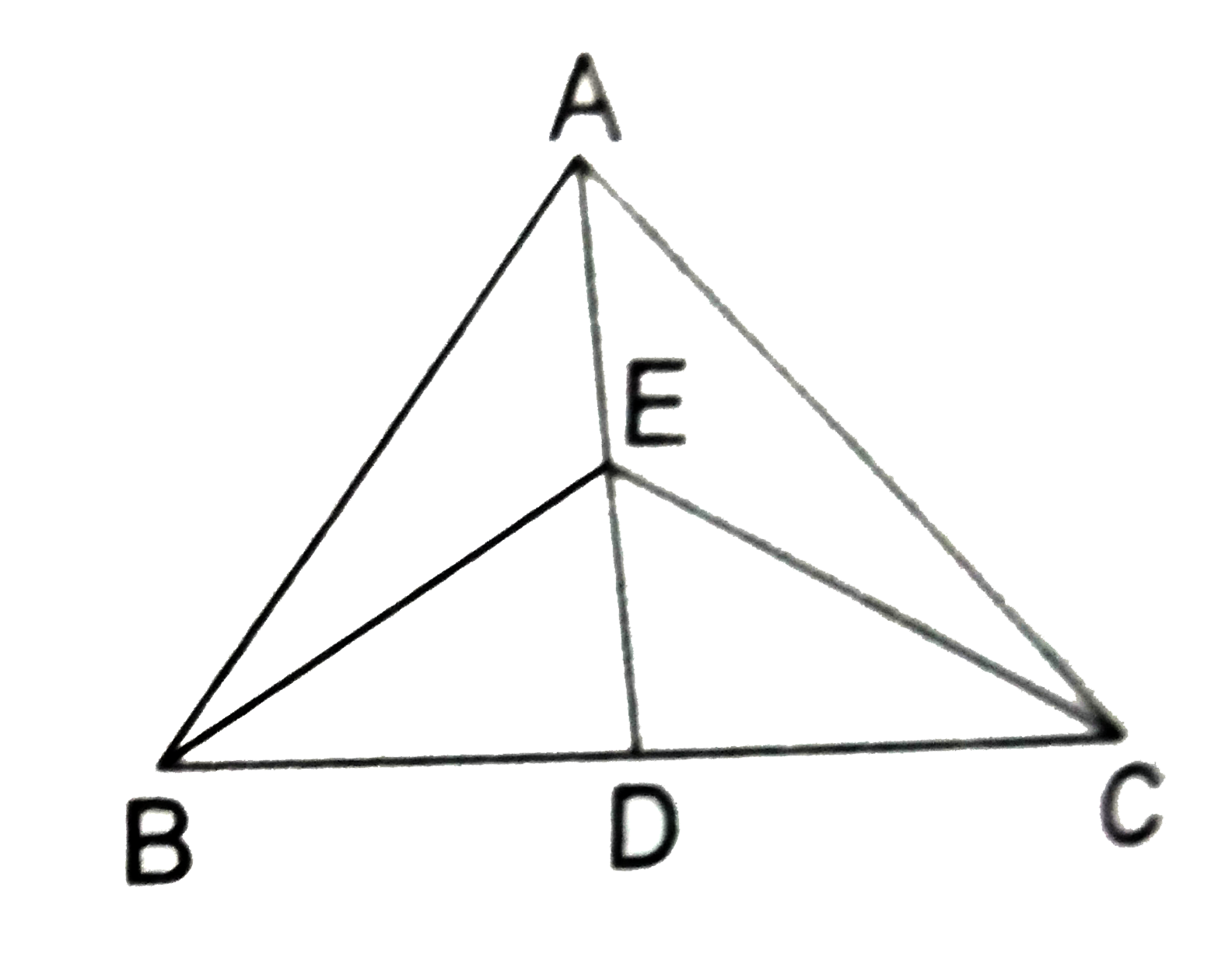
.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).
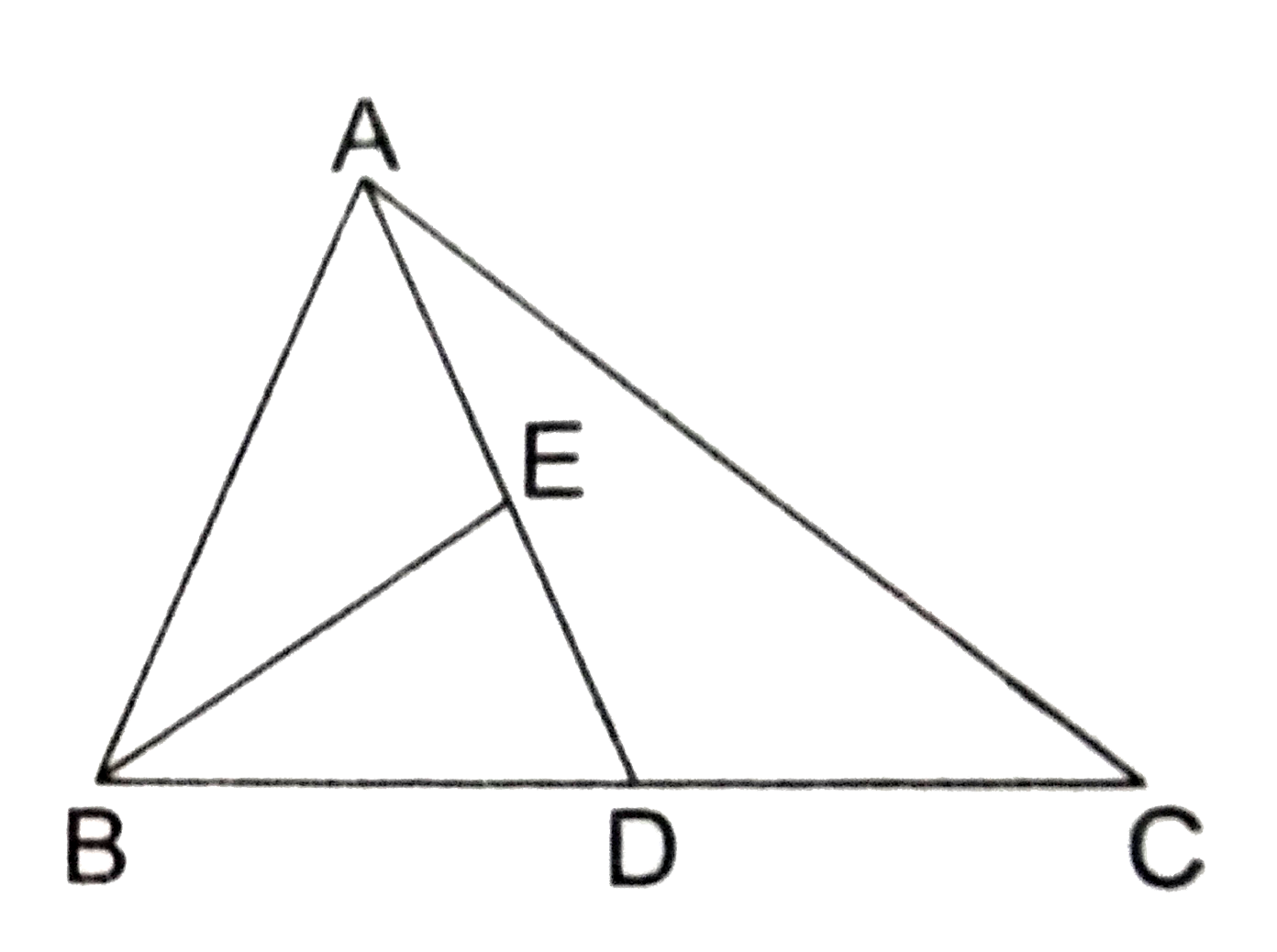 View Solution
View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
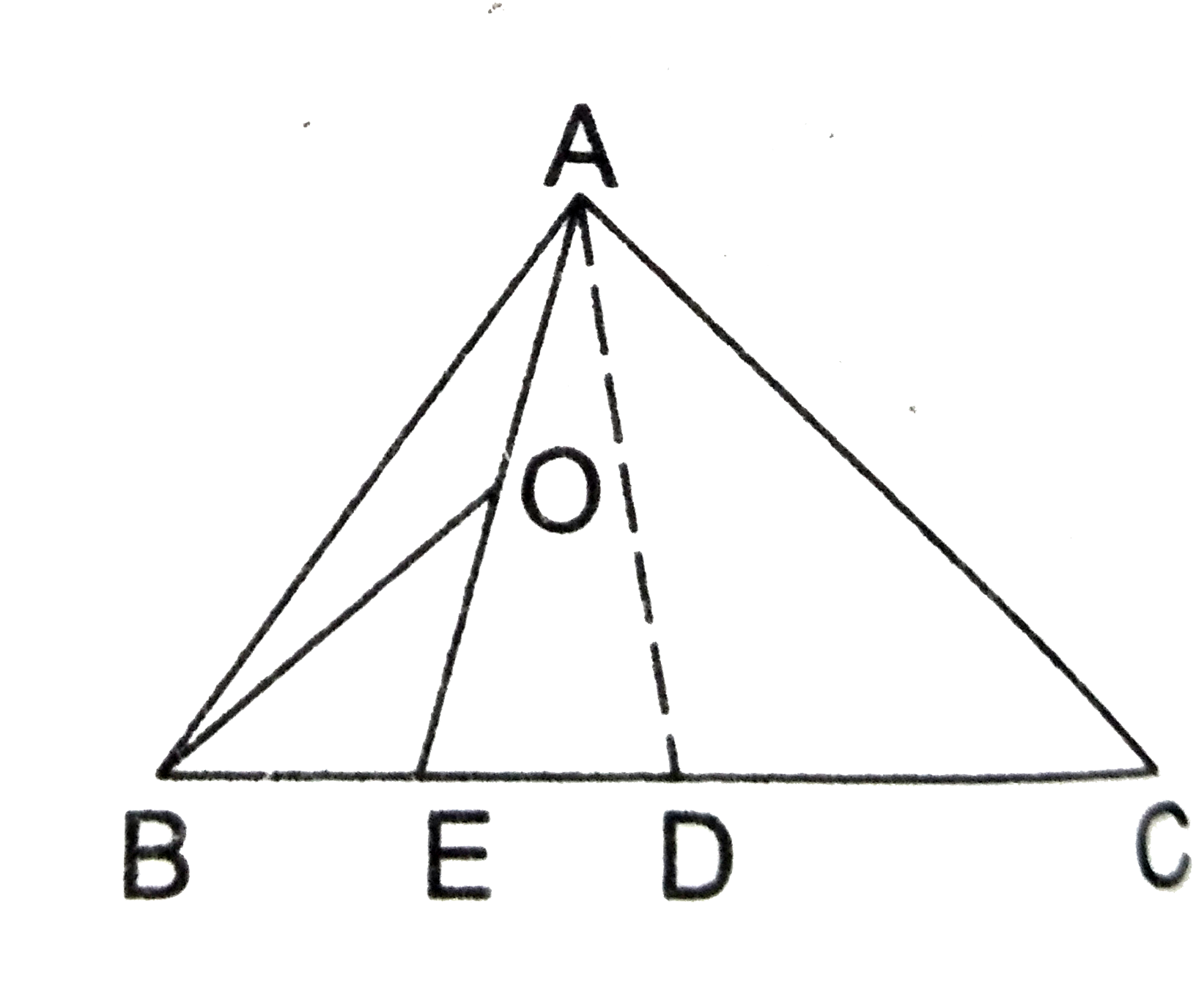 View Solution
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View SolutionIf vertex A of triangle ABC is (3,5) and centroid is (−1,2), then find the midpoint of side BC.
View SolutionIn the adjoining figure, BD||CA, E is the midpoint of CA and BD=12CA. Prove that
ar(△ABC)=2ar(△DBC).
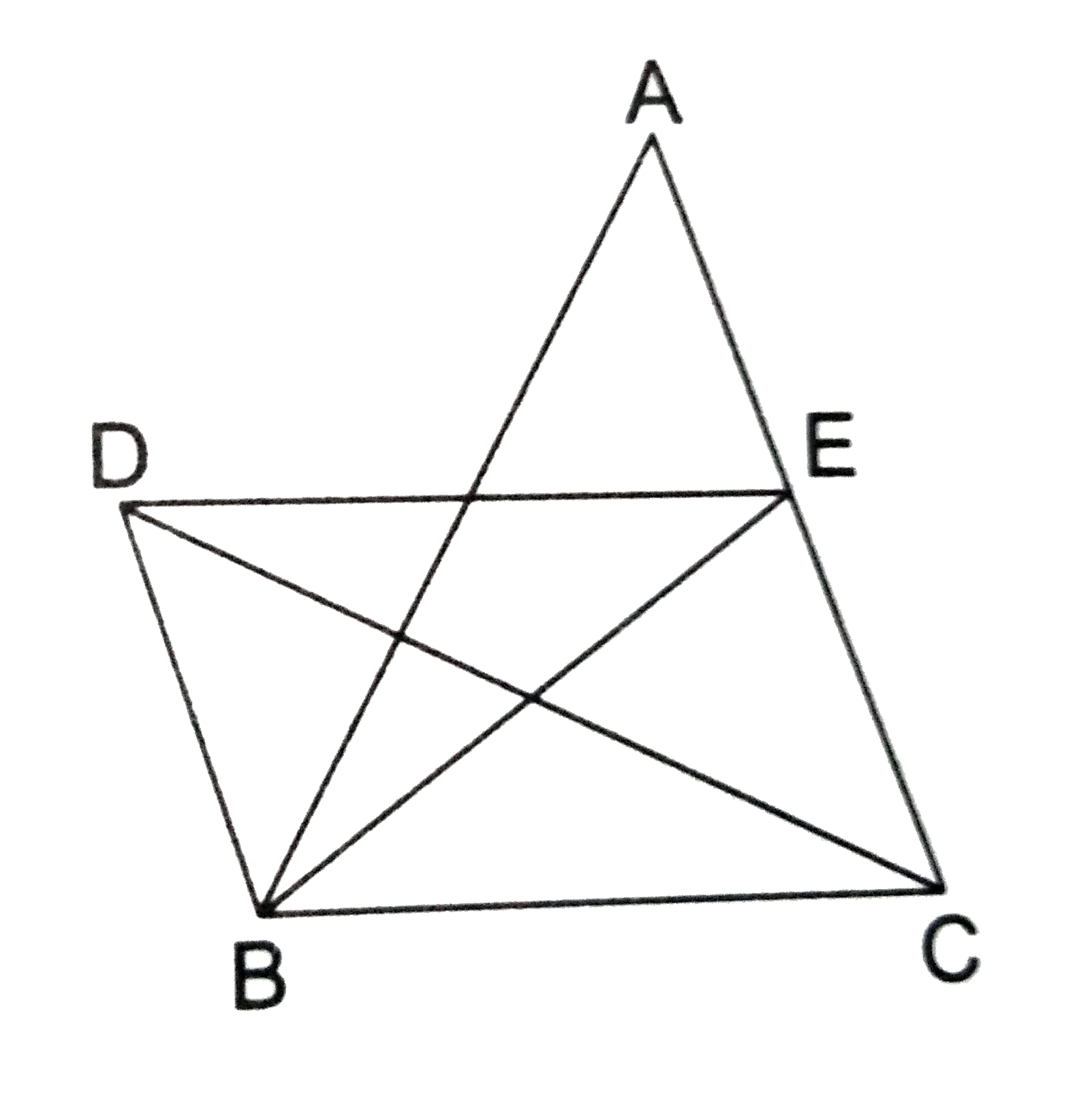 View Solution
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
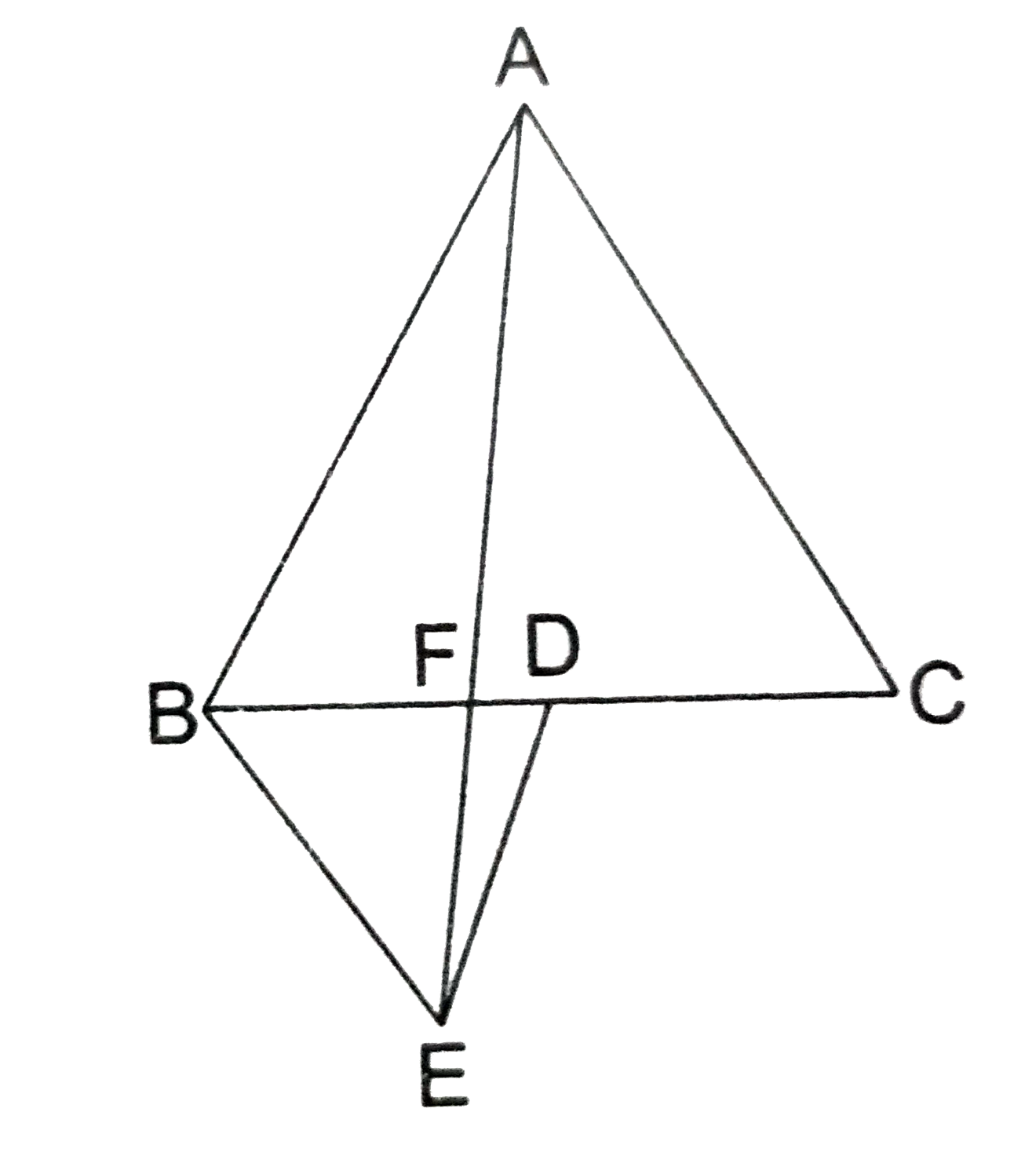 View Solution
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)View SolutionIn a ABC,E is the mid-point of median AD. Show that ar(BED)=14ar(ABC)
View Solution

