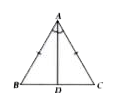
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
To prove that line AD bisects angles A and D in triangle ABC, where AB = AC and BD = CD, we will follow these steps:
Step 1: Identify the Given Information
We have triangle ABC, which is isosceles with AB = AC. We also have point D such that BD = CD.
Hint: Write down all the given information clearly to visualize the problem.
Step 2: Draw the Triangles
Draw triangle ABC with point D on line BC such that BD = CD. This creates two triangles: ABD and ACD.
Hint: Visualizing the triangles will help you understand the relationships between their sides and angles.
Step 3: Use the Given Equalities
From the problem, we know:
- AB = AC (sides of triangle ABC)
- BD = CD (sides of triangle BDC)
- AD is common to both triangles ABD and ACD.
Hint: Identify all equal sides and common sides in the triangles.
Step 4: Apply the Side-Side-Side (SSS) Congruence Criterion
Since we have:
- AB = AC (given)
- BD = CD (given)
- AD = AD (common side)
We can conclude that triangles ABD and ACD are congruent by the SSS criterion.
Hint: Remember that if two triangles have all three sides equal, they are congruent.
Step 5: Conclude About the Angles
Since triangles ABD and ACD are congruent, their corresponding angles are equal:
- ∠BAD = ∠DAC (angles opposite to equal sides)
- ∠BDA = ∠CDA (angles opposite to equal sides)
Hint: Use the property of congruent triangles that states corresponding angles are equal.
Step 6: State the Conclusion
Since ∠BAD = ∠DAC, line AD bisects angle A. Similarly, since ∠BDA = ∠CDA, line AD also bisects angle D.
Hint: Summarize your findings clearly to reinforce the proof.
Final Statement
Thus, we have proved that line AD bisects both angles A and D in triangle ABC.
---
We have triangle ABC, which is isosceles with AB = AC. We also have point D such that BD = CD.
Draw triangle ABC with point D on line BC such that BD = CD. This creates two triangles: ABD and ACD.
From the problem, we know:
- AB = AC (sides of triangle ABC)
- BD = CD (sides of triangle BDC)
- AD is common to both triangles ABD and ACD.
Since we have:
- AB = AC (given)
- BD = CD (given)
- AD = AD (common side)
Since triangles ABD and ACD are congruent, their corresponding angles are equal:
- ∠BAD = ∠DAC (angles opposite to equal sides)
- ∠BDA = ∠CDA (angles opposite to equal sides)
Since ∠BAD = ∠DAC, line AD bisects angle A. Similarly, since ∠BDA = ∠CDA, line AD also bisects angle D.
Thus, we have proved that line AD bisects both angles A and D in triangle ABC.
Topper's Solved these Questions
- CONGRUENCEBOOK - RS AGGARWALCHAPTER - CONGRUENCEEXERCISE - EXERCISE
18 Videos
- COLLECTION AND ORGANISATION OF DATA (MEAN, MEDIAN AND MODE)BOOK - RS AGGARWALCHAPTER - COLLECTION AND ORGANISATION OF DATA (MEAN, MEDIAN AND MODE)EXERCISE - EXERCISE 21C
5 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (True/False)
4 Videos
Similar Questions
In the adjoinng figure, ΔABC is an isoceless triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠Aand∠D.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
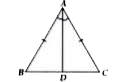
AD⊥BC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
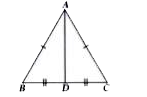 Prove that:
Prove that:
∠BAD=∠CAD
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
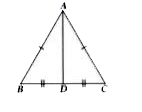 Prove that:
Prove that:
ΔADB≅ΔADC
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. If BM⊥ACandCN⊥AB, prove that:
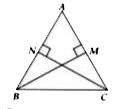
BM = CN
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
∠B=∠C
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
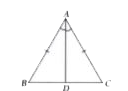
ΔADB≅ΔADC
View Solution
