If two triangles have their corresponding angles equal, are they always congruent? If not, draw two triangles which are not congruent but which have their corresponding angles equal
To determine whether two triangles with corresponding angles equal are always congruent, we can analyze the situation step by step.
1. Understanding Congruence:
- Two triangles are said to be congruent if they can be perfectly overlaid on each other, meaning all their corresponding sides and angles are equal.
2. Identifying Corresponding Angles:
- For two triangles to have corresponding angles equal, each angle in one triangle must match with an angle in the other triangle. For example, if triangle ABC has angles A, B, and C, then triangle PQR must have angles P, Q, and R such that:
- Angle A = Angle P
- Angle B = Angle Q
- Angle C = Angle R
3. Exploring the Possibility of Non-Congruent Triangles:
- To check if triangles with equal angles are always congruent, we can draw two triangles with the same angles but different side lengths.
4. Drawing Triangle ABC:
- Let’s draw triangle ABC with the following angles:
- Angle A = 70°
- Angle B = 60°
- Angle C = 50°
- Assign the sides: AB = 4 units, AC = 3 units, and BC = 6 units.
5. Drawing Triangle PQR:
- Now, let’s draw triangle PQR with the same angles:
- Angle P = 70°
- Angle Q = 60°
- Angle R = 50°
- Assign different side lengths: PQ = 10 units, PR = 12 units, and QR = 8 units.
6. Comparing the Two Triangles:
- Now, we compare triangle ABC and triangle PQR. Although their corresponding angles are equal, the lengths of their sides differ.
- When we try to overlay triangle ABC on triangle PQR, they do not cover each other completely.
7. Conclusion:
- Since triangle ABC and triangle PQR have equal corresponding angles but different side lengths, they are not congruent. Therefore, we conclude that two triangles with equal corresponding angles are not always congruent.
Final Statement:
- Answer: No, two triangles with corresponding angles equal are not always congruent. We have demonstrated this by drawing two triangles (ABC and PQR) that have equal angles but different side lengths.
- Two triangles are said to be congruent if they can be perfectly overlaid on each other, meaning all their corresponding sides and angles are equal.
- For two triangles to have corresponding angles equal, each angle in one triangle must match with an angle in the other triangle. For example, if triangle ABC has angles A, B, and C, then triangle PQR must have angles P, Q, and R such that:
- Angle A = Angle P
- Angle B = Angle Q
- Angle C = Angle R
- To check if triangles with equal angles are always congruent, we can draw two triangles with the same angles but different side lengths.
- Let’s draw triangle ABC with the following angles:
- Angle A = 70°
- Angle B = 60°
- Angle C = 50°
- Assign the sides: AB = 4 units, AC = 3 units, and BC = 6 units.
- Now, let’s draw triangle PQR with the same angles:
- Angle P = 70°
- Angle Q = 60°
- Angle R = 50°
- Assign different side lengths: PQ = 10 units, PR = 12 units, and QR = 8 units.
- Now, we compare triangle ABC and triangle PQR. Although their corresponding angles are equal, the lengths of their sides differ.
- When we try to overlay triangle ABC on triangle PQR, they do not cover each other completely.
- Since triangle ABC and triangle PQR have equal corresponding angles but different side lengths, they are not congruent. Therefore, we conclude that two triangles with equal corresponding angles are not always congruent.
- Answer: No, two triangles with corresponding angles equal are not always congruent. We have demonstrated this by drawing two triangles (ABC and PQR) that have equal angles but different side lengths.
Topper's Solved these Questions
- CONGRUENCEBOOK - RS AGGARWALCHAPTER - CONGRUENCEEXERCISE - EXERCISE
18 Videos
- COLLECTION AND ORGANISATION OF DATA (MEAN, MEDIAN AND MODE)BOOK - RS AGGARWALCHAPTER - COLLECTION AND ORGANISATION OF DATA (MEAN, MEDIAN AND MODE)EXERCISE - EXERCISE 21C
5 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (True/False)
4 Videos
Similar Questions
Knowledge Check
Assertion : If we draw two triangles with angles 30∘,70∘and80∘ and the length of the sides of one triangle be different than that of the corresponding sides of the other triangle then two triangles are not congruent.
Reason : If two triangles are constructed which have all corresponding angles equal but have unequal corresponding sides, then two triangles cannot be congruent to each other.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.For the given triangles, write the correspondence, if they are congruent.
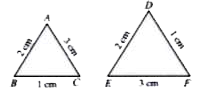 AΔABC≅ΔDEFBΔABC≅ΔEDFCΔABC≅ΔFDEDnot congruent
AΔABC≅ΔDEFBΔABC≅ΔEDFCΔABC≅ΔFDEDnot congruentTwo isosceles triangles have their corresponding angles equal and their areas are in the ratio 25:36. The ratio of their corresponding heights is
A25:36B36:25C5:6D6:5
All the triangles equal in area are congruent.
View SolutionTwo right angles are congruent
View SolutionIf two arcs of a circle are congruent; then corresponding chords are equal
View SolutionIf two chords of a congruent circle are equal; then their corresponding arcs are also equal.
View SolutionAssertion (A) : If two triangles are congruent their corresponding angles are equal.
Reason (R ) : Area of two congruent triangles are equal.
View Solution
