In the given figure, CE||BA. If ∠BAC=70∘ and ∠ECD=50∘,find ∠ACB.
The correct Answer is:60∘
To solve the problem step by step, we will use the properties of parallel lines and angles.
1. Identify Given Information:
- CE is parallel to BA (CE || BA).
- Angle BAC = 70°.
- Angle ECD = 50°.
2. Use Alternate Angles Property:
- Since CE is parallel to BA, the angles BAC and ACE are alternate interior angles.
- Therefore, angle ACE = angle BAC = 70°.
3. Set Up the Equation for Angles on a Straight Line:
- On the straight line CE, the sum of angles ACE, ACB, and ECD must equal 180°.
- This can be expressed as:
Angle ACE+Angle ACB+Angle ECD=180°
4. Substitute Known Values:
- Substitute the known values into the equation:
70°+Angle ACB+50°=180°
5. Combine Like Terms:
- Combine the angles on the left side:
120°+Angle ACB=180°
6. Solve for Angle ACB:
- Isolate angle ACB:
Angle ACB=180°−120°=60°
Final Answer:
- Angle ACB = 60°.
---
- CE is parallel to BA (CE || BA).
- Angle BAC = 70°.
- Angle ECD = 50°.
- Since CE is parallel to BA, the angles BAC and ACE are alternate interior angles.
- Therefore, angle ACE = angle BAC = 70°.
- On the straight line CE, the sum of angles ACE, ACB, and ECD must equal 180°.
- This can be expressed as:
Angle ACE+Angle ACB+Angle ECD=180°
- Substitute the known values into the equation:
70°+Angle ACB+50°=180°
- Combine the angles on the left side:
120°+Angle ACB=180°
- Isolate angle ACB:
Angle ACB=180°−120°=60°
- Angle ACB = 60°.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (M.C.Q)7videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (Fill in the blanks)5videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE C(M.C.Q)38videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONGRUENCEEXERCISE - EXERCISE18videos
CONGRUENCE
- BOOK - RS AGGARWALCHAPTER - DECIMALSEXERCISE - TEST PAPER-3(D)5videos
DECIMALS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, PQ || RS, ∠PAB = 60∘ and ∠ACS = 100∘ . Then, ∠BAC = ?
A40∘B60∘C80∘D50∘ - Question 2 - Select One
In the given figure, ∠A - 50∘, CE || BA and ∠ECD -60∘. Then, ZACB = ?
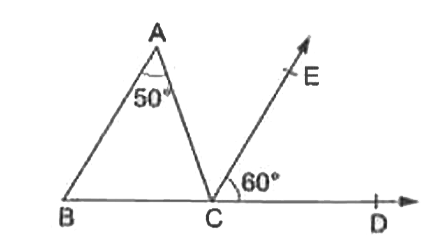 A50∘B60∘C70∘D80∘
A50∘B60∘C70∘D80∘ - Question 3 - Select One
In the given figure, if EC∣∣AB,∠ECD=70∘,∠BDO=20∘, then ∠OBD is
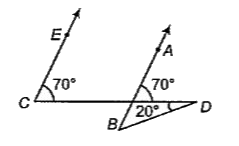 A70∘B60∘C50∘D20∘
A70∘B60∘C50∘D20∘
In a rhombus ABCD, if ∠ACB=40∘, then ∠ADB=(a) 70∘ (b) 45∘ (c) 50∘ (d) 60∘
View SolutionIn the given figure, ∠ABC=69∘,∠ACB=31∘,find ∠BDC
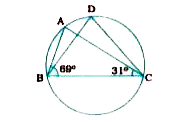 View Solution
View SolutionIn the given figure, AB∣∣CD. Prove that ∠BAE−∠ECD=∠AEC.
View SolutionIn the given figure, AM⊥BC and AN is the bisector of ∠A If ∠ABC=70∘ and ∠ACB=20∘, find ∠MAN.
View Solution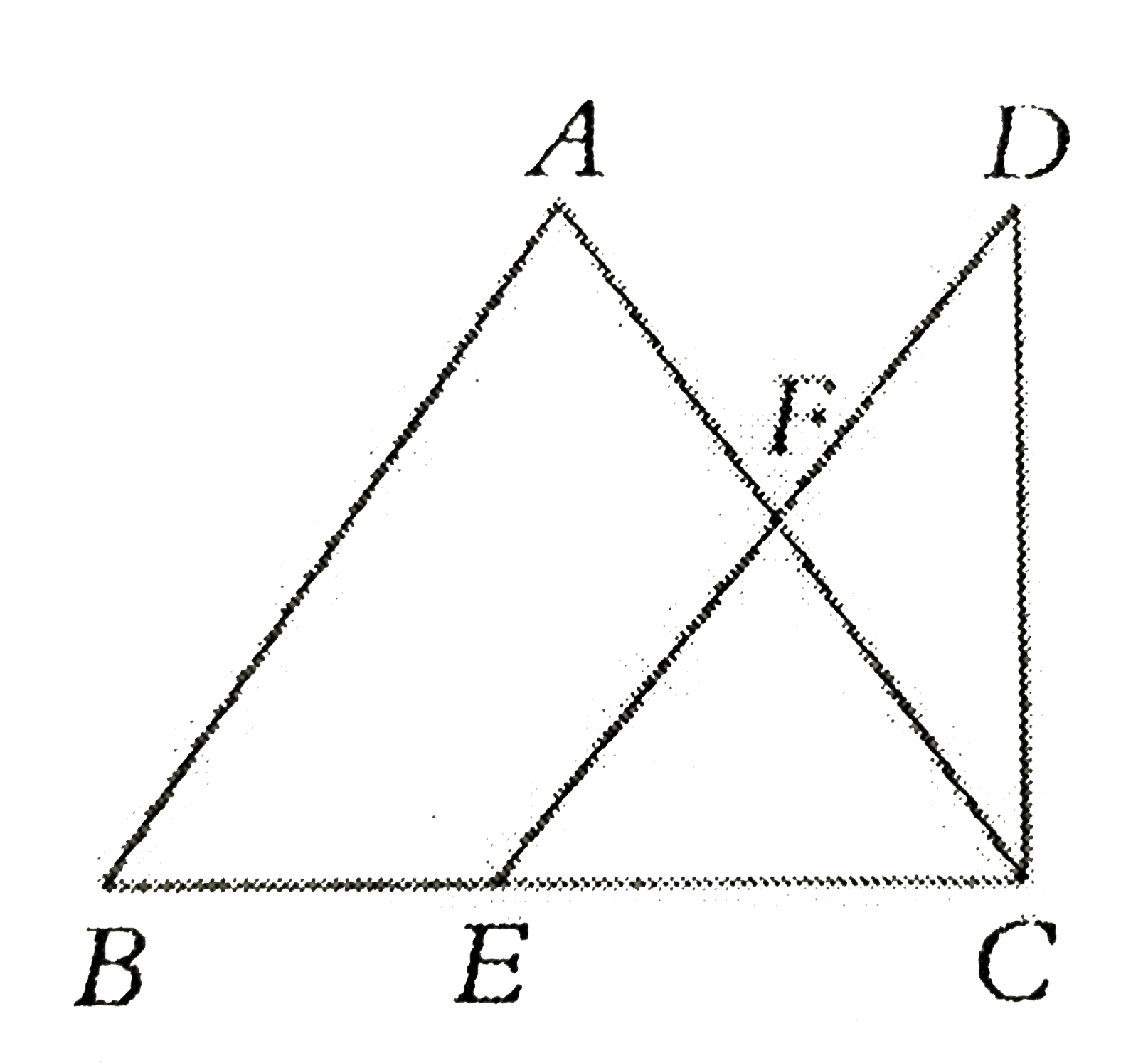
In the given figurs, ∠BAC=70∘,∠BCD=80∘,∠EFC=80∘ and ∠ABC=60∘. How many isoscles triangles are there in the given figure ?View Solution

