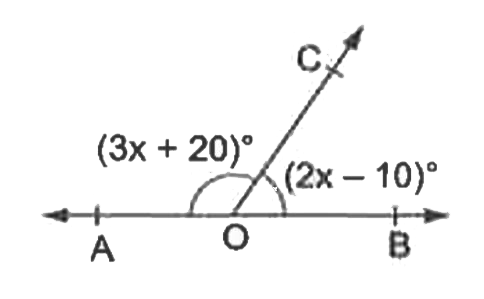
In the given figure, AOB is a straight line and OC is a ray such that ∠AOC=(3x+20)∘ and ∠BOC=(2x−10)∘. Find the value of x and hence find (i) ∠AOC
(ii)∠BOC
Video Solution
Text Solution
The correct Answer is:x=34
∠AOC=122∘
x=34
∠BOC=58∘
|
Answer
Step by step video, text & image solution for In the given figure, AOB is a straight line and OC is a ray such that /_AOC = (3x+20)^(@) and /_BOC = (2x - 10)^(@). Find the value of x and hence find (i) /_AOC (ii)/_BOC <Br> by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (M.C.Q)7videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - TEST PAPER (Fill in the blanks)5videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE C(M.C.Q)38videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - CONGRUENCEEXERCISE - EXERCISE18videos
CONGRUENCE
- BOOK - RS AGGARWALCHAPTER - DECIMALSEXERCISE - TEST PAPER-3(D)5videos
DECIMALS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, AOB is a straight line and the ray OC stands on it. If ∠BOC = 132∘, then ∠AOC = ?
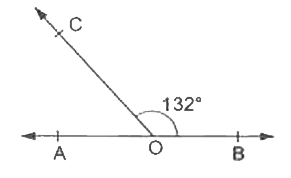 A68∘B48∘C42∘Dnone of these
A68∘B48∘C42∘Dnone of these - Question 2 - Select One
In the given figure, AOB is a straight line, ∠AOC = (3x−8)∘, ∠COD = 50∘ and ∠BOD = (x+10)∘. The value of x is
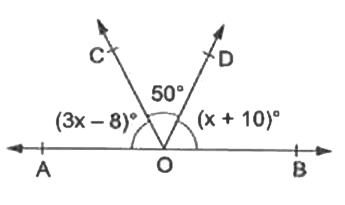 A32B42C36D52
A32B42C36D52 - Question 3 - Select One
In the given figure, AOB is a straight line, ∠AOC=56∘ and ∠BOC=x∘. The value of x is
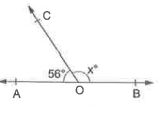 A34B44C144D124
A34B44C144D124
In the given figure,XOY is a straight line,find the value of x
View SolutionIn a figure , AB is a straight line , Find (x+y):
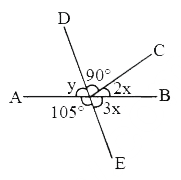 View Solution
View SolutionIn the given figure .AOB is straight a straight line and the ray OC stands on it.If ∠AOC=64∘and∠BOC=x∘,Find the value of x.
View SolutionIn the adjoining figure, AOB is a straight line. Find the value of x.
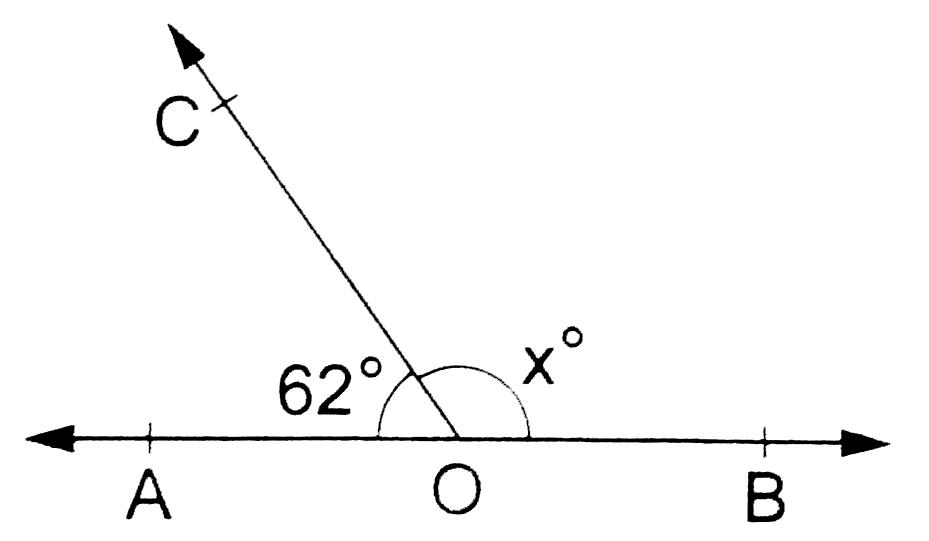 View Solution
View SolutionIn the following figure AOB is astraight line. Find the value of x
View Solution



